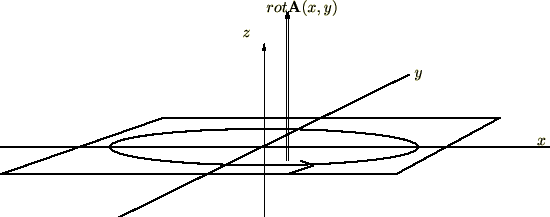
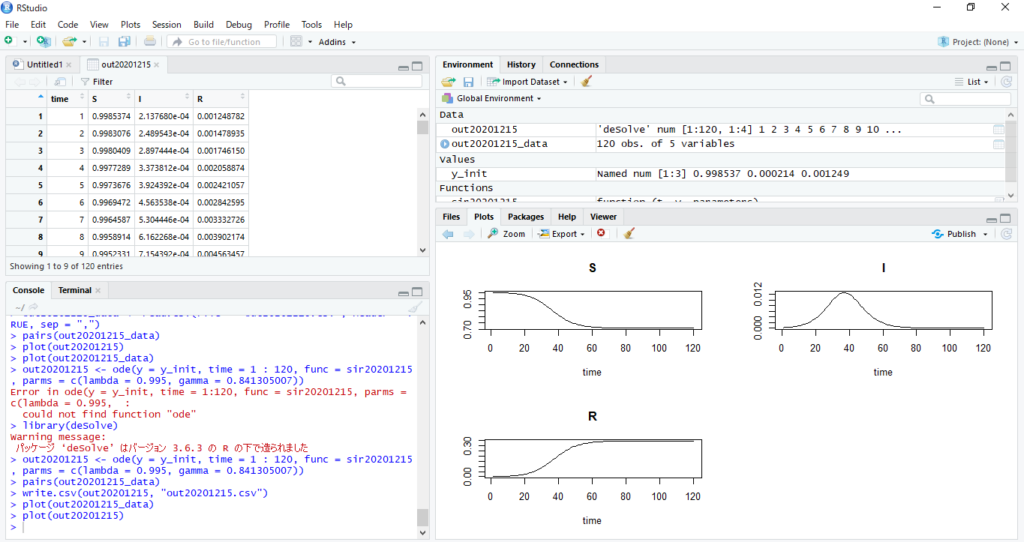
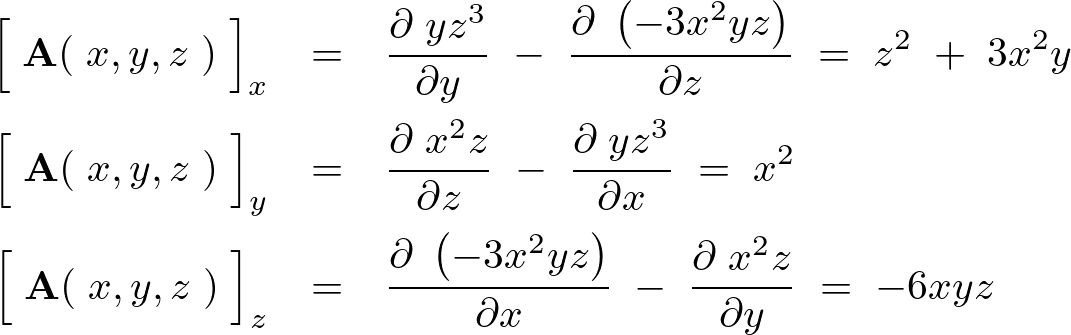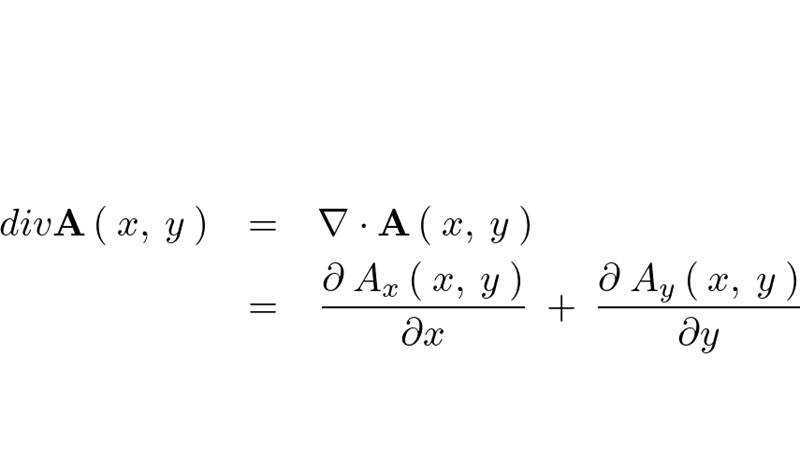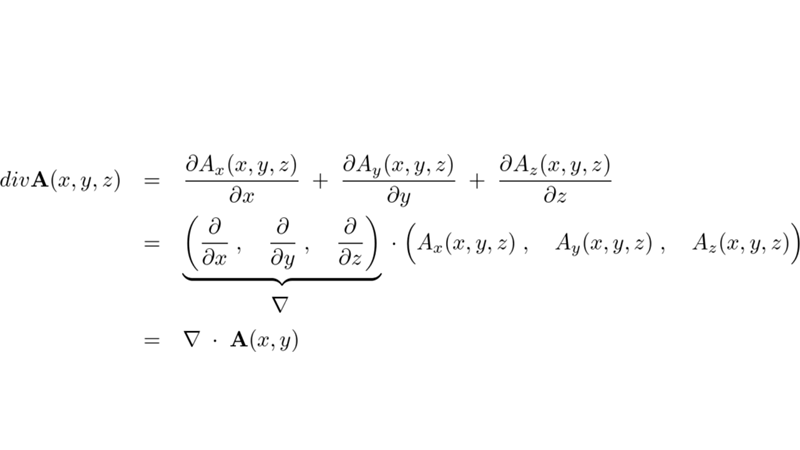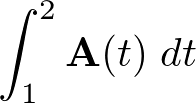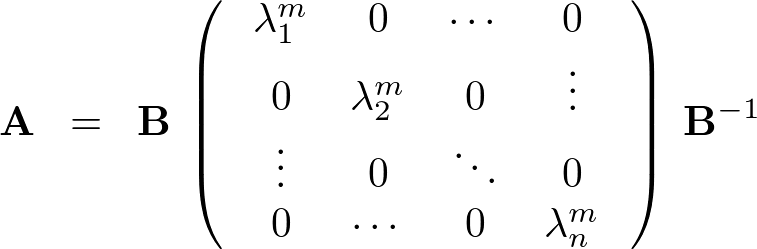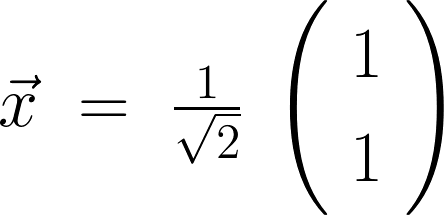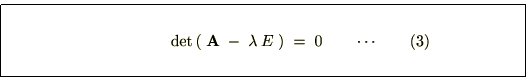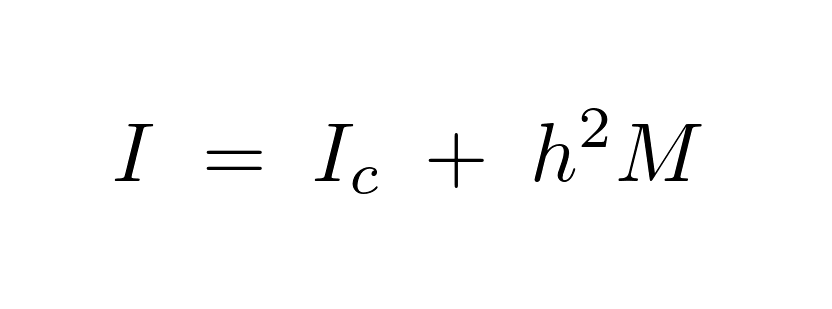三次元ベクトル場および発散についての補足
三次元におけるベクトル表現は、
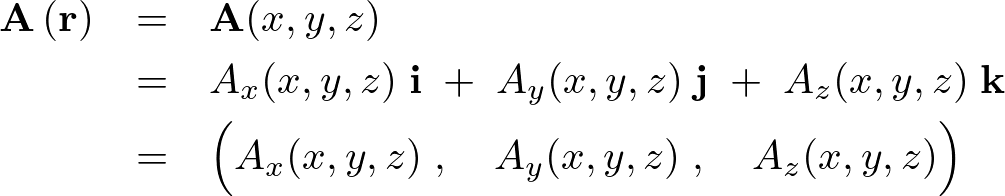
であるので、その発散は次のようになります。
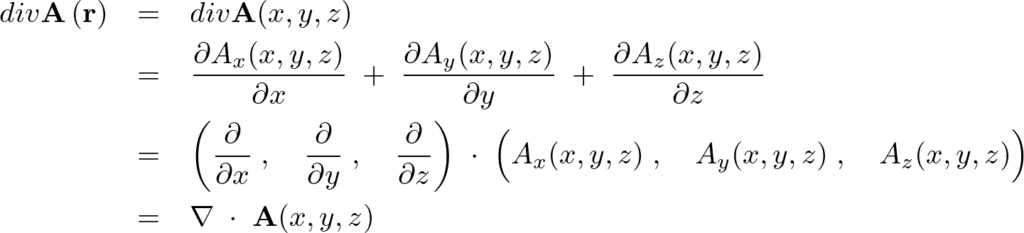
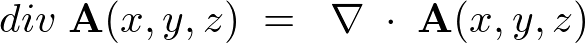
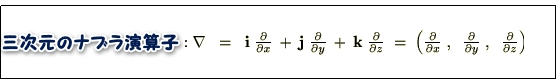
以上のことによりベクトル場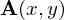 の発散(ダイバージェンス)というのは、
の発散(ダイバージェンス)というのは、
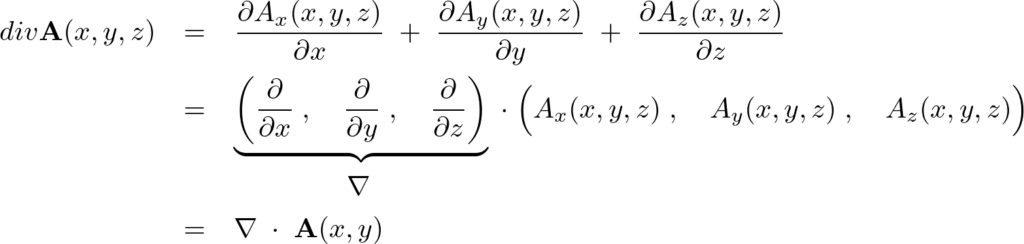
ということなので、

ということがいえます(内積なのでスカラー量)。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-

微分積分学
カテゴリー
-
導関数
カテゴリー
-
偏微分
カテゴリー
-

長方形板の慣性モーメント
カテゴリー
-

円柱の慣性モーメント
カテゴリー
-

半球体の慣性モーメント
カテゴリー
-
-
-
-
三次元ベクトル場および発散についての補足
カテゴリー : 三次元ベクトル場、発散についての補足三次元ベクトル場の発散(ダイバージェンス)に関して、ナブラとベクトル場の内積との関係について考察してみましょう…
-
-
-
-
-
-