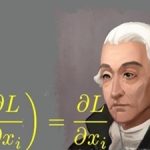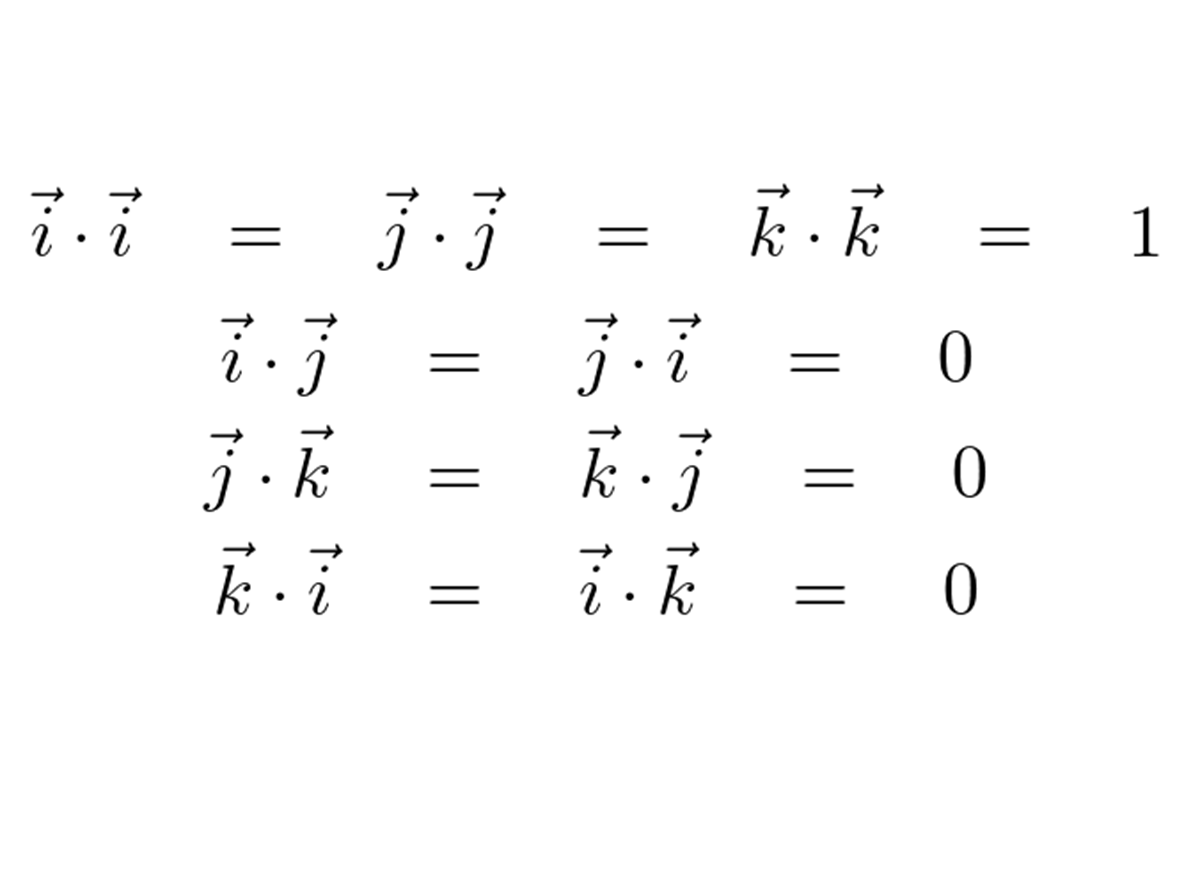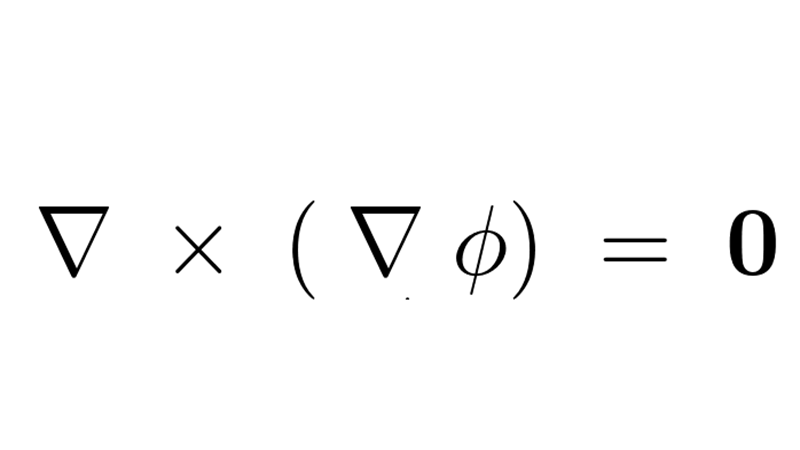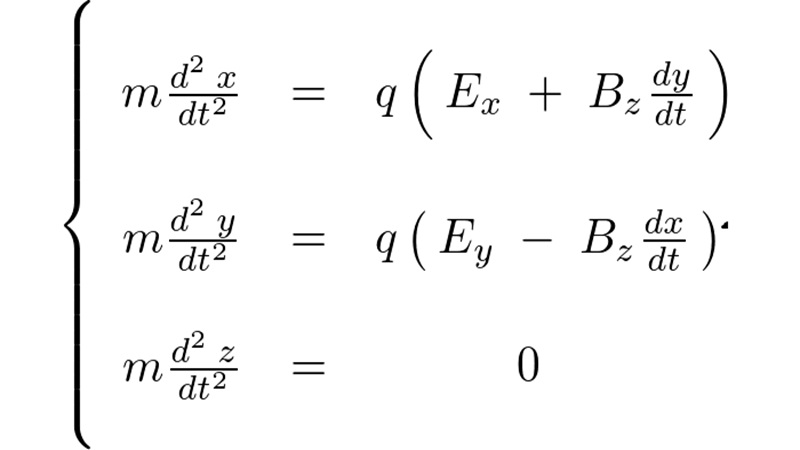三次元ベクトル場および発散についての補足
三次元におけるベクトル表現は、
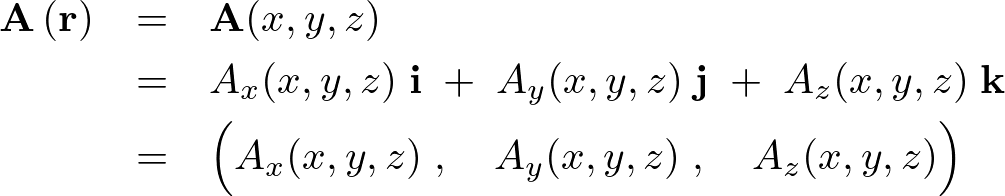
であるので、その発散は次のようになります。
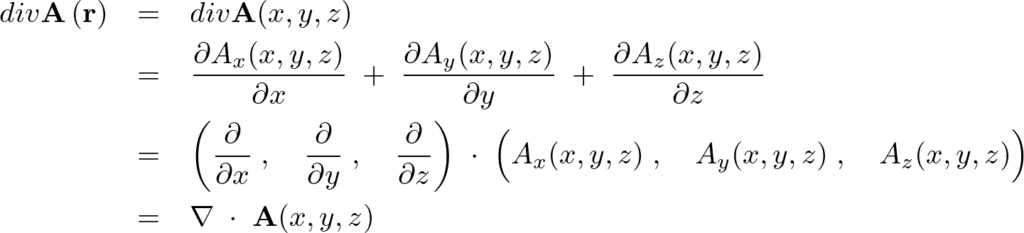
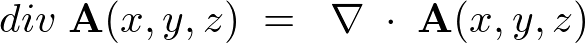
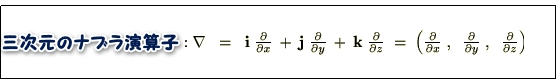
以上のことによりベクトル場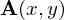 の発散(ダイバージェンス)というのは、
の発散(ダイバージェンス)というのは、
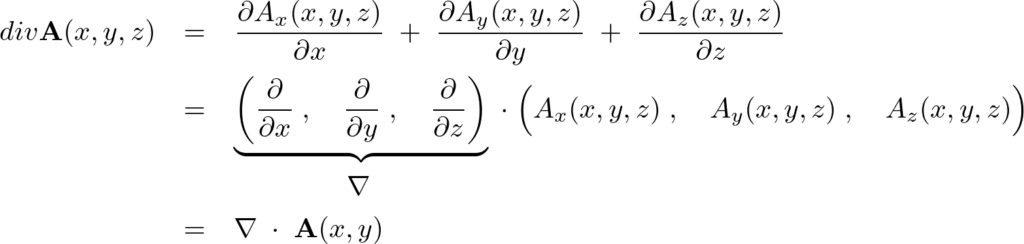
ということなので、

ということがいえます(内積なのでスカラー量)。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-

ルータ1台での基本操作
カテゴリー
-
テラタームの設定
カテゴリー
-
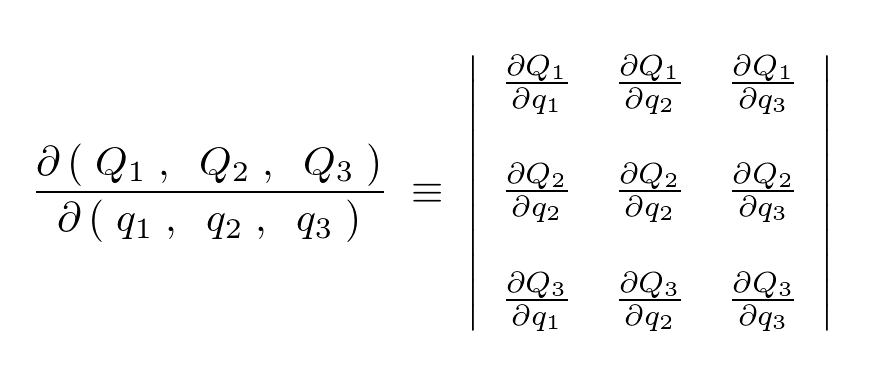
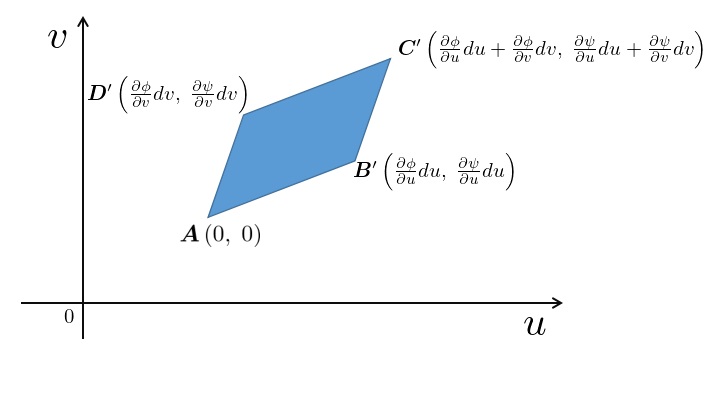
dvの計算法-ヤコビアンを使うやり方
カテゴリー
-

円盤の慣性モーメント①
カテゴリー
-
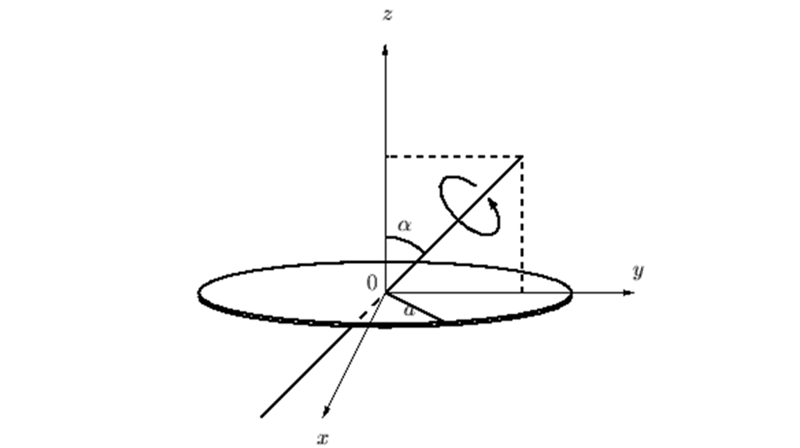
円盤の慣性モーメント②
カテゴリー
-
-
-
-
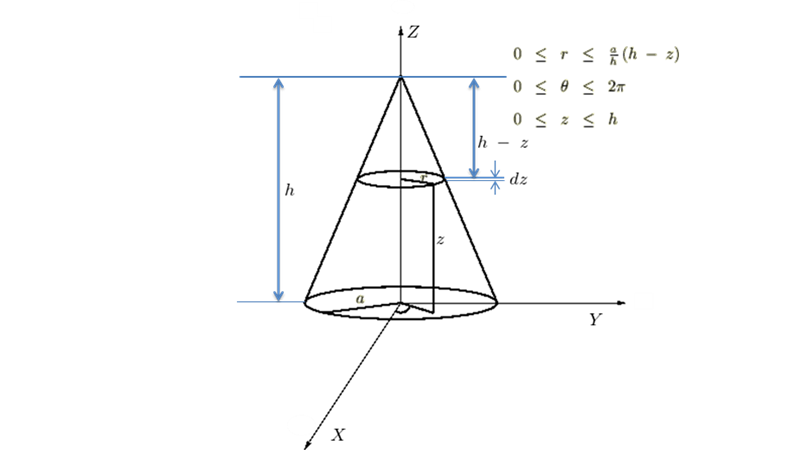
円錐の頂点、底面、重心に関する慣性モーメント
カテゴリー : 円錐の頂点、底面、重心周りの慣性モーメントこのセクションでは平行軸の定理を利用した円錐の頂点周り、円錐底面に平行で中心点を通る軸周りに関する慣性モーメン…
-
-
-
PythonによるCSV取り込み
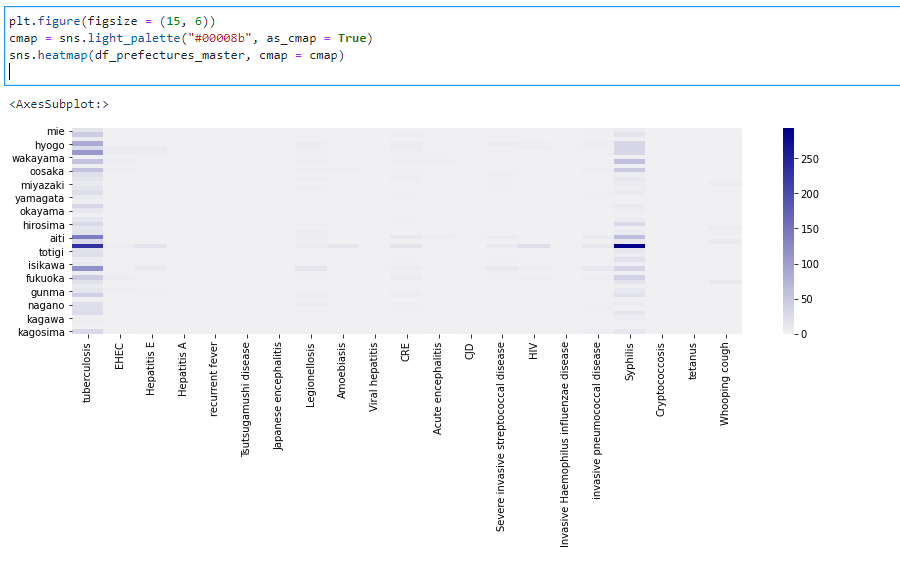
カテゴリー : PythonによるCSVファイル取り込みサンプルにするデータはIDWR速報データの五類感染症に関して都道府県別発生件数を週ごとにまとめられたCSVファ…
-
-
-