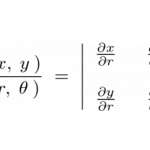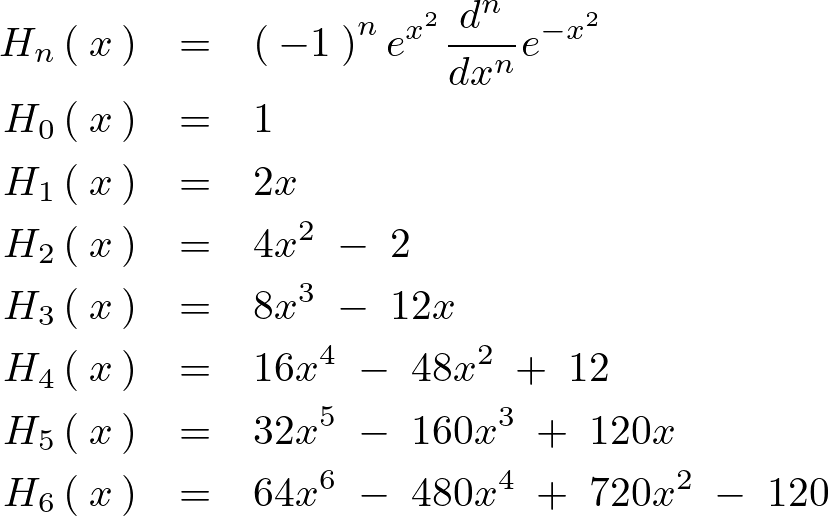三次元ベクトル場および発散についての補足
三次元におけるベクトル表現は、
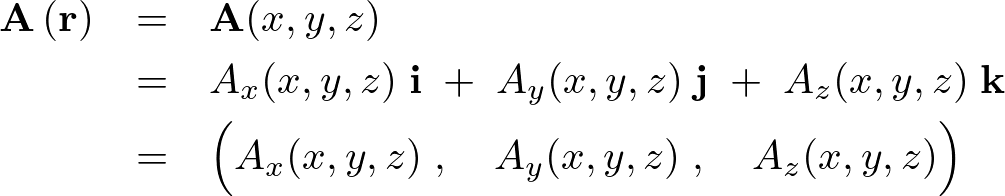
であるので、その発散は次のようになります。
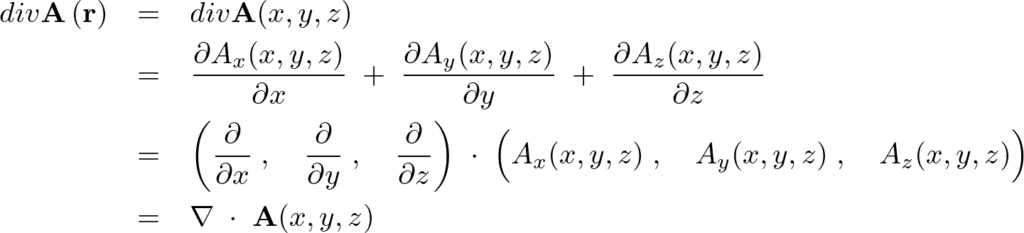
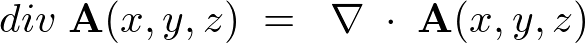
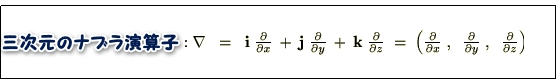
以上のことによりベクトル場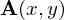 の発散(ダイバージェンス)というのは、
の発散(ダイバージェンス)というのは、
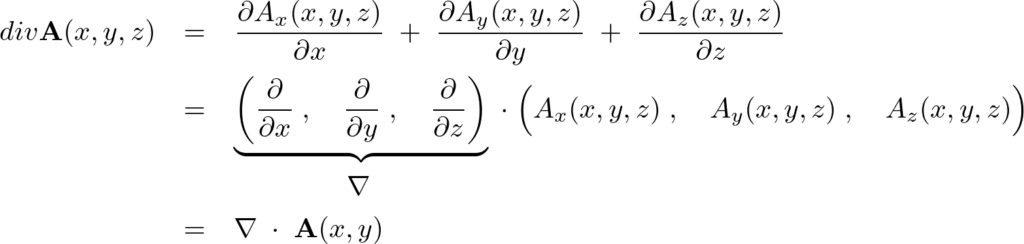
ということなので、

ということがいえます(内積なのでスカラー量)。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
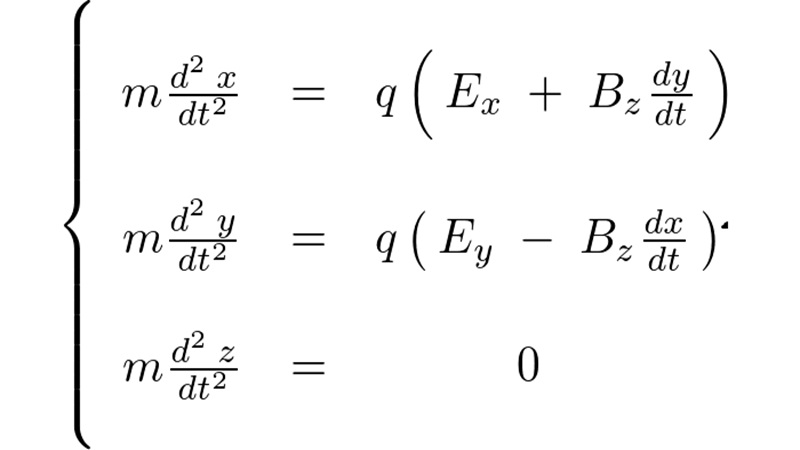
ベクトル解析 ━ 補遺
カテゴリー
-
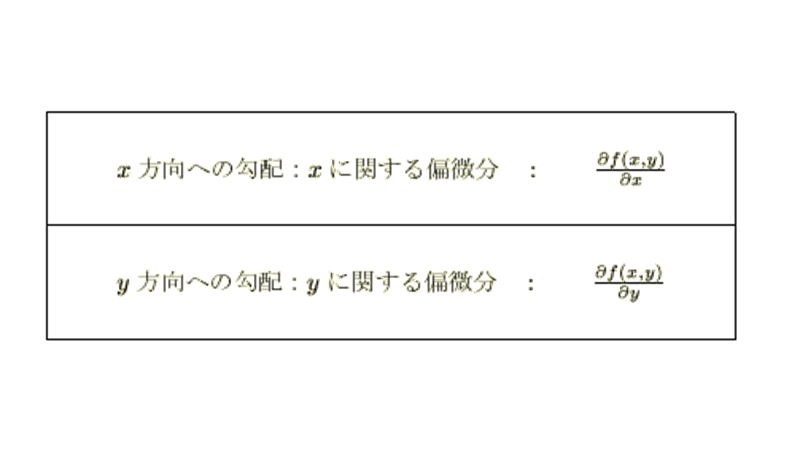
スカラー場、ベクトル場
カテゴリー
-

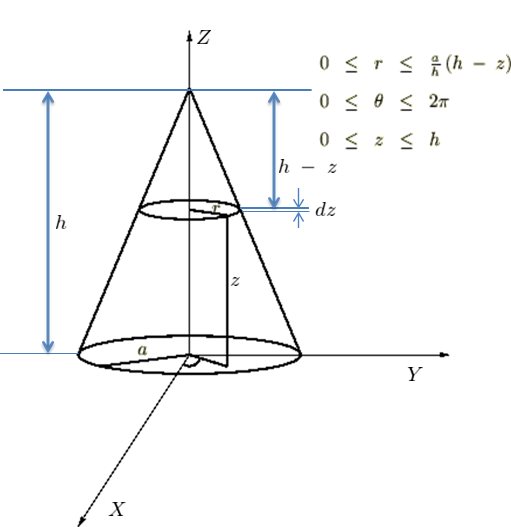
微小体積要素dvの計算
カテゴリー
-

dv計算法-答え
カテゴリー
-
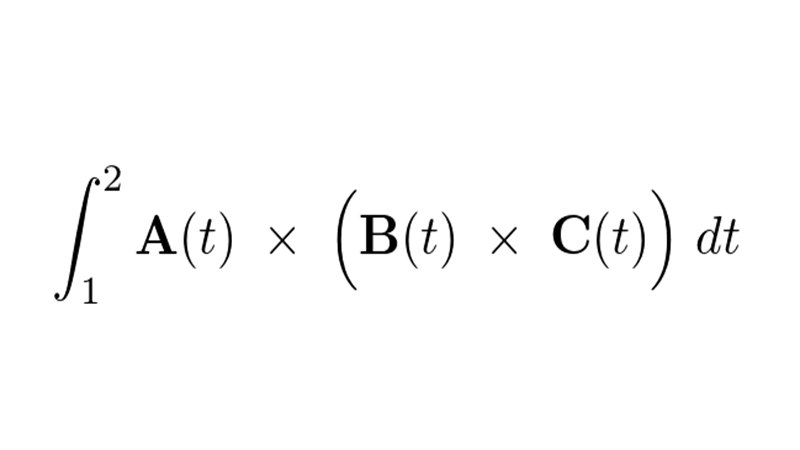
ベクトル積分問題の答え
カテゴリー
-
-
diff-eq.comスケールアップマイグレーション2
カテゴリー : diff-eq.comスケールアップマイグレーション2前回からの続きになります。この度のマイグレーションは運用を始めてから2か月弱ほどたっていないという異例の速さに…
-
diff-eq.comスケールアップマイグレーション1
カテゴリー : diff-eq.comスケールアップマイグレーション1微分方程式いろいろを本格稼働してからたった2か月弱しかたっていませんが運用していてわかったのですがサーバレスポ…
-
-
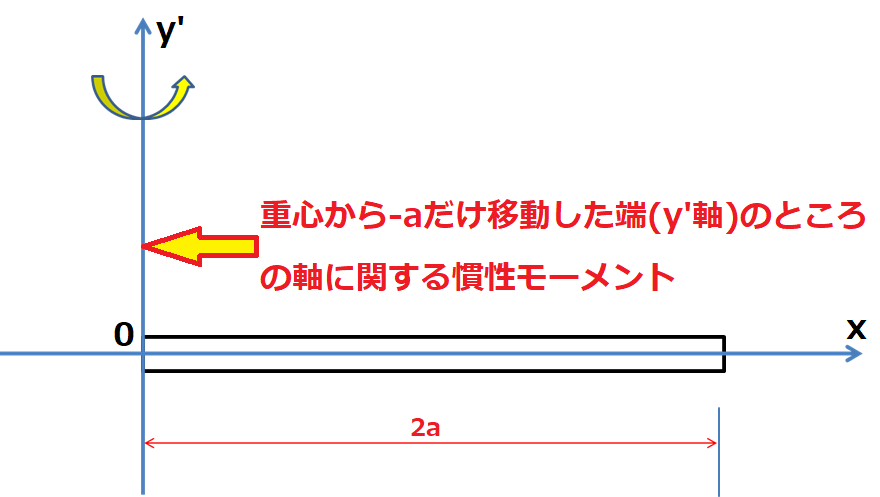
平行軸の定理と棒の慣性モーメント
カテゴリー : 平行軸定理を使った棒の慣性モーメント重心の位置を0とする-aからaまでの棒の距離の長さを2a、棒の左へ-aだけ移動した端を通る軸に関する慣性モーメ…
-
-
-
-
-