ベクトル場の回転(ローテーション)
ベクトル場の回転 ━ ローテーション
このセクションでは、ベクトル場の回転というものを考えます。
まず、ベクトル場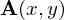 の回転というのは、
の回転というのは、
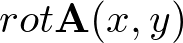
と書きます。
ベクトル場の発散(ダイバージェンス)はスカラー場でしたが、ベクトル場の回転(ローテーション)は、ベクトル場になります。
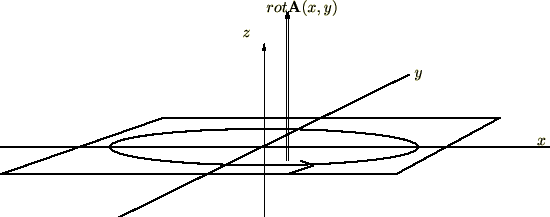
「ベクトル場の回転」という(ベクトルの)向きは、![]() 軸のプラス方向の、右ねじの進む向きになります。
軸のプラス方向の、右ねじの進む向きになります。

“発散”において勾配を調べるときに使った領域を、今度は次のようにノズルをもった形に変形させてみましょう。
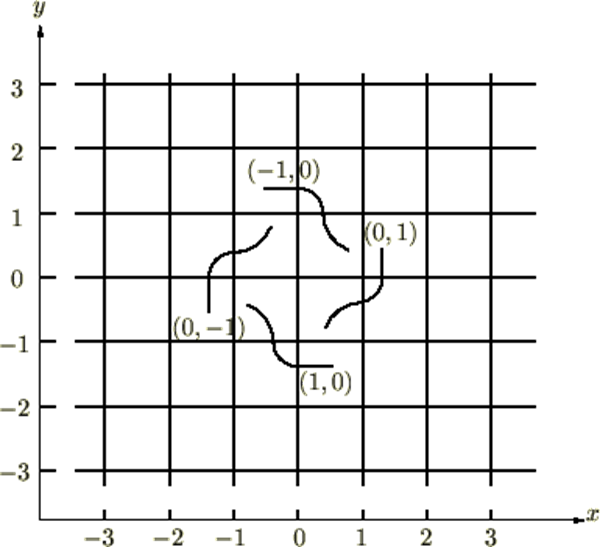
さらにそのノズルにおいてはそれぞれの方向に対するベクトル値を書き入れます。
このとき左右の出口からの寄与と上下の出口からの寄与は別々に考えてください。
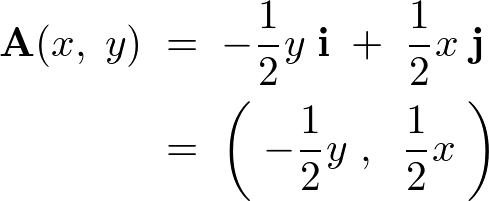
において、座標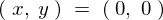 を中心としたときのベクトル場の回転は、
を中心としたときのベクトル場の回転は、

なので、
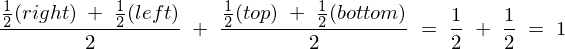
さらに、ベクトル成分を用いた表現においては次のようになります。
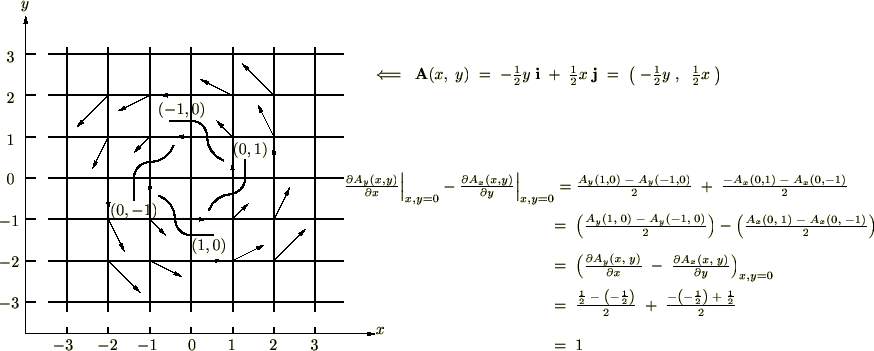
ここで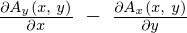 について考察してみましょう。
について考察してみましょう。
三次元のベクトル場、
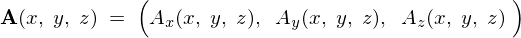
の外積ベクトル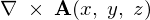 の
の![]() 成分
成分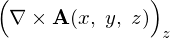 によって与えられます。
によって与えられます。
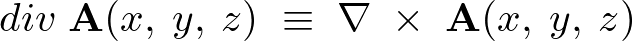
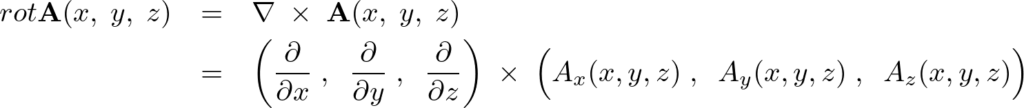
各成分ごとに表せば、
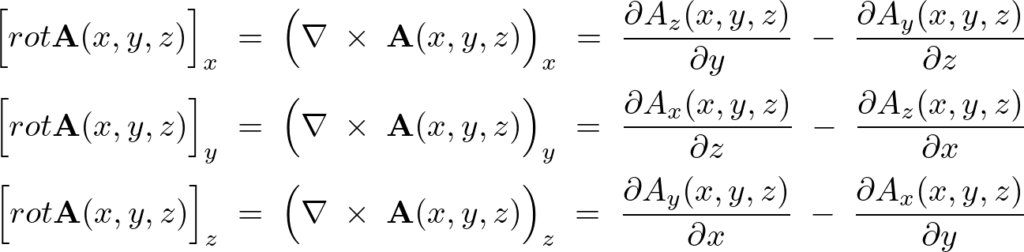
以上のことを踏まえると、二次元ベクトル場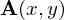 というのは三次元ベクトル場、
というのは三次元ベクトル場、
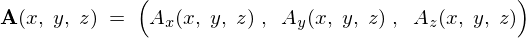
においての、
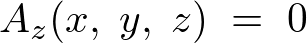
であり、さらには、

ということがいえるかと思います。
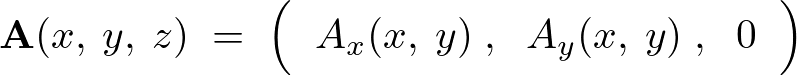
この時において、
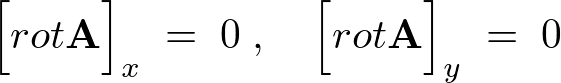
なので、
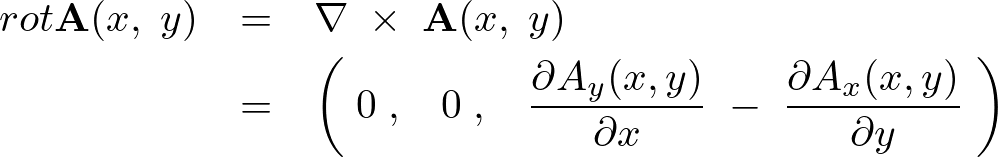
これらにより、『二次元ベクトル場の回転』においては、これは常に![]() 成分のみを持つので結局のところ、
成分のみを持つので結局のところ、
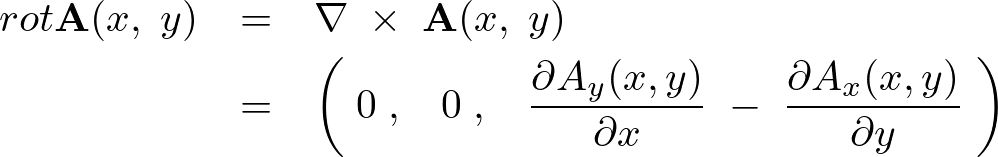
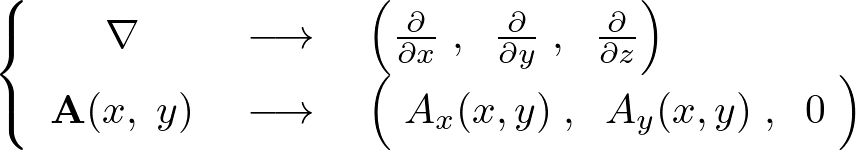
となります。
つまり、二次元ベクトル場の回転(ローテーション)を考えるときでも、『二次元ベクトル場』を『三次元ベクトル場の特別な場合』と考える必要があります。
まとめると、
一般の三次元ベクトル場、
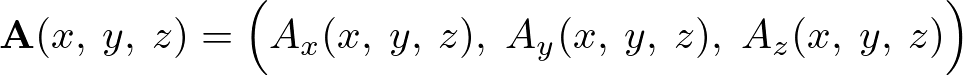
における回転(ローテーション)は、『三次元のナブラ』と『三次元のベクトル場』の外積で与えられるベクトル、
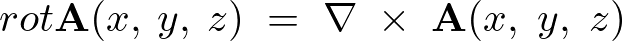
にほかなりません。
【ベクトル場の回転に関する補足】
『ベクトル場の回転』
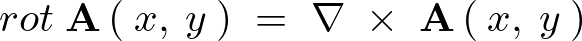
はベクトル場になります。
そのベクトルに関して注意する点を軽くまとめると、
| 方向: | ベクトル場の回転に合わせて回る右ねじの進む向き |
| 大きさ: | 回転の強さ |
になります。
二次元ベクトル場の場合においてはつねに、
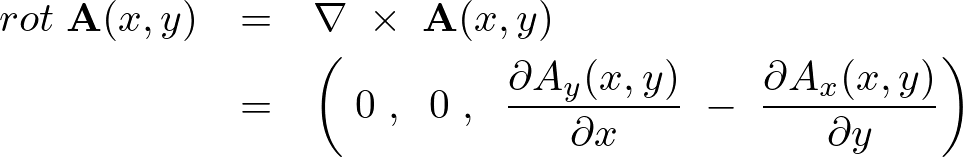
が成り立ちます。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
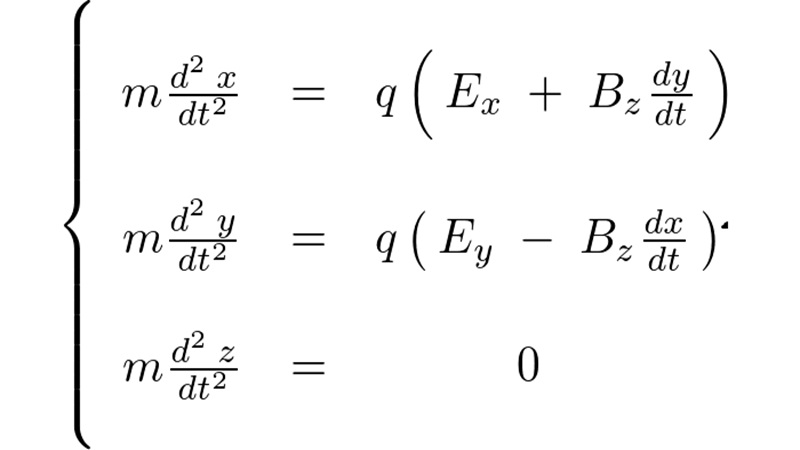
ベクトル解析 ━ 補遺
カテゴリー
-
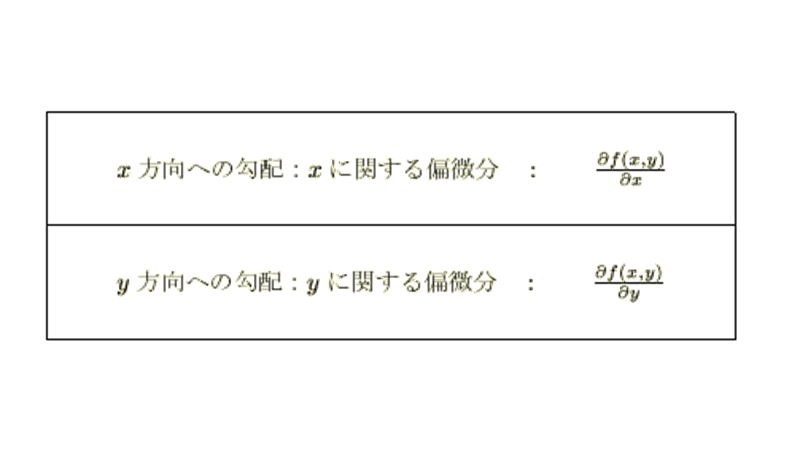
スカラー場、ベクトル場
カテゴリー
-

微小体積要素dvの計算
カテゴリー
-

dv計算法-答え
カテゴリー
-
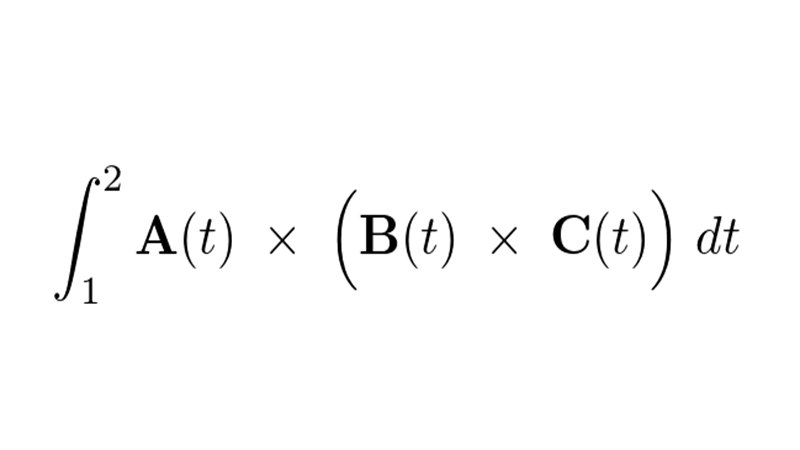
ベクトル積分問題の答え
カテゴリー
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-