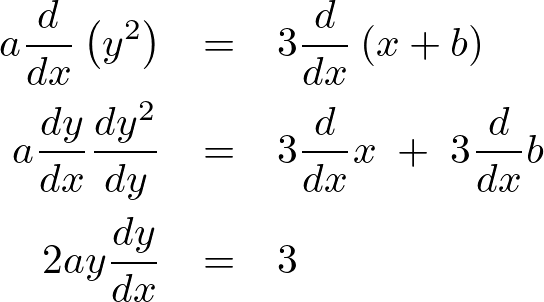電磁気学への応用
電磁気学応用の簡単な例
ROTの計算
物理科の一年次に習うベクトル解析でのローテーション計算に関しての記述はほとんどの場合3行3列の行列式に表記しているかと思います。
たいていの場合、実際の計算ではサラスで解くかあるいは行列表記ではないこの公式のようなもの(↓)を解説しているのが主流かと思います。
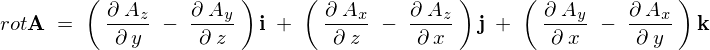
こういったのは覚えるのに大変苦労するので、このローテーション計算に関する行列式をスカラー三重積のセクションにおいて出てきた『行列式展開法』を使ってやってみることにしましょう。
式の変形
ローテーションの行列式の表記はこのようだったと思います。
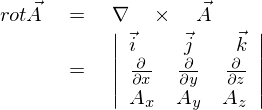
これをスカラー三重積のセクションにおいてやった配置換えを同じように施します。
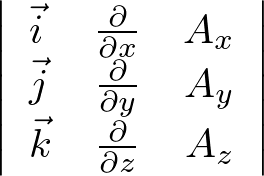
のようにします。
これを行列式展開法によって次のように計算していきます。
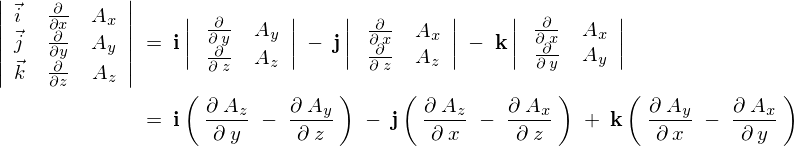
ここで右辺第2項の中の偏微分を入れ替え(符号を変化)、基本ベクトルの位置も上記表記通りにすれば結局のところ次のようになります。
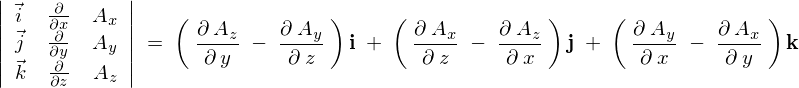
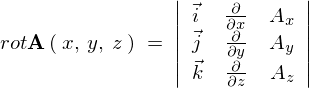
荷電粒子の運動方程式
一定の強さ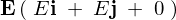 の電場に磁束密度
の電場に磁束密度![]() の一定の強さの磁場が
の一定の強さの磁場が![]() 方向にかけられているとします。
方向にかけられているとします。
この座標系においての荷電粒子の運動方程式を求めてみましょう。
まず、考えている座標系においての電場と磁場のそれぞれ3方向の成分を次のようなものとします。
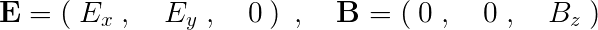
クーロン力があるときのローレンツ力は次のように表されます。
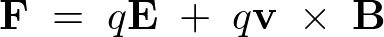
右辺第2項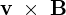 を計算すると、
を計算すると、
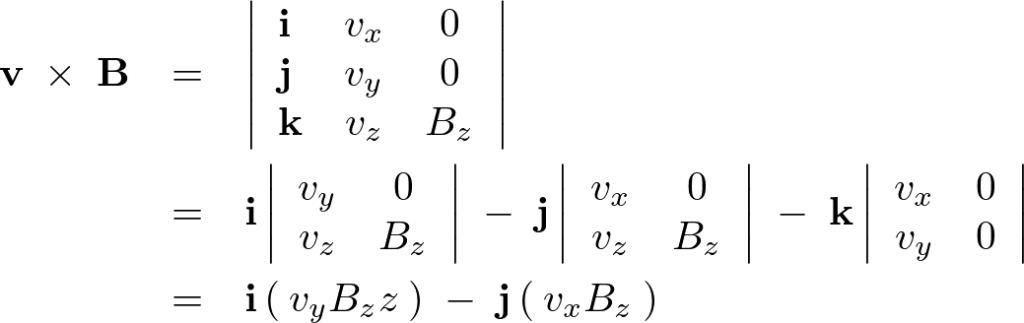
ローレンツの式に代入します。
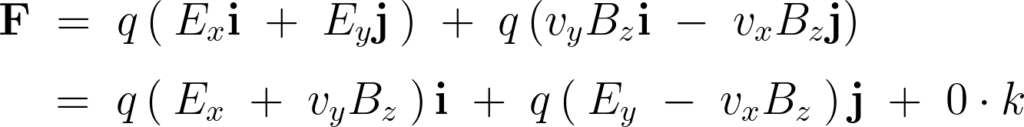
さらにベクトル が、
が、
であるならば、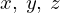 のそれぞれの方向に対して次のようになります。
のそれぞれの方向に対して次のようになります。
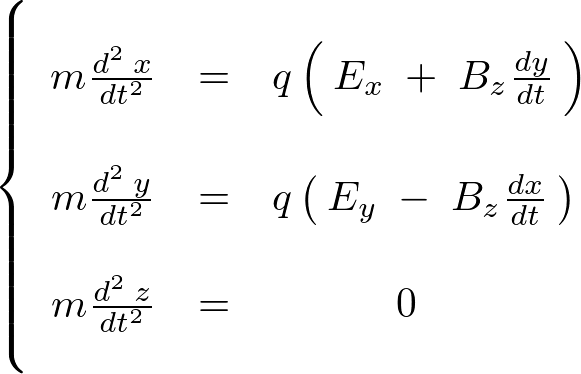

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
TikZ
カテゴリー
-

年金終価係数
カテゴリー
-
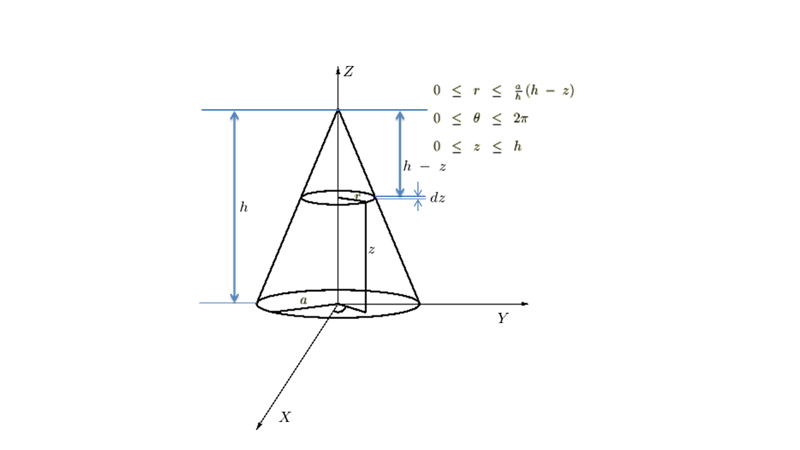
円錐の慣性モーメント
カテゴリー
-
diff-eq.comスケールアップアップマイグレーション3
-
多次元量ヤコビアン
カテゴリー
-
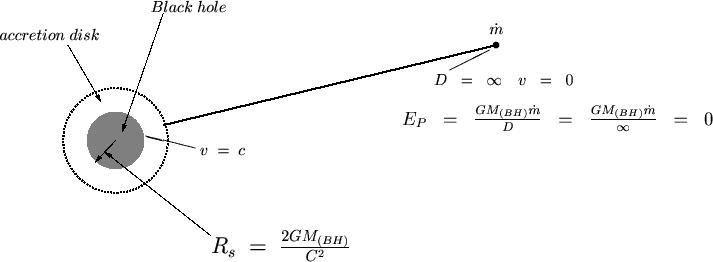
クェーサーとブラックホール
カテゴリー
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-