ベクトル解析その他重要な性質
ベクトル場の回転においての重要な性質を、ROT計算を利用して証明してみましょう。
その①
あるベクトル場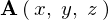 があったとします。
があったとします。
そのベクトル場に対して、
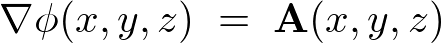
を満たすようなスカラー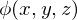 が存在するためには、
が存在するためには、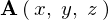 に対してどういった条件が必要かを考えます。
に対してどういった条件が必要かを考えます。

まず次のように勾配ベクトルに対し、ナブラを左側から作用(オペレート)させます。
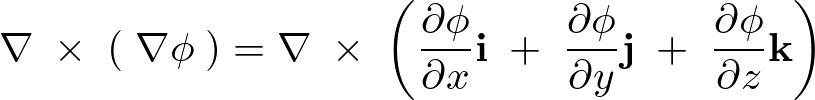
実際に計算していきます。
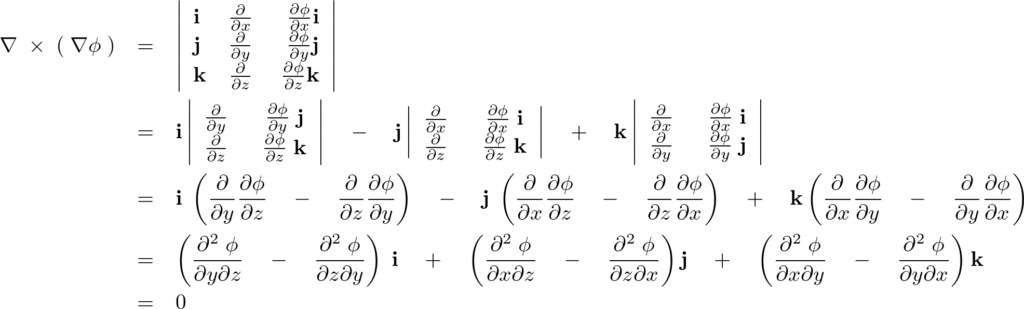

これにより、
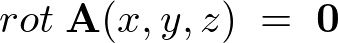
が必要条件になります。
ポイント
回転のあるベクトル場は勾配ベクトルになり得ない
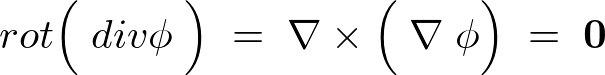
その②
あるベクトル場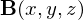 に対して、
に対して、
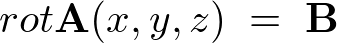
を満たすようなベクトル場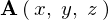 が存在するためには、
が存在するためには、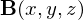 に対してどのような条件が必要かを考えてみましょう。
に対してどのような条件が必要かを考えてみましょう。

あるベクトル場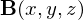 が、
が、
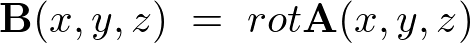
と書けるとします。
このとき、ベクトル場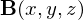 のダイバージェンスを考えると、
のダイバージェンスを考えると、
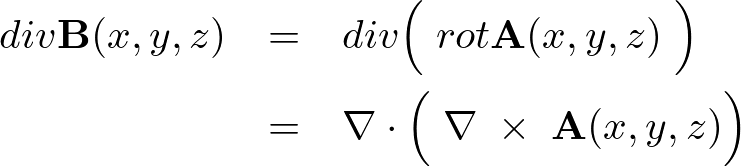
です。したがって、
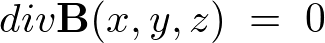
が必要条件になります。
実際にこれを証明してみましょう。
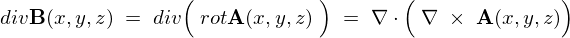
より、
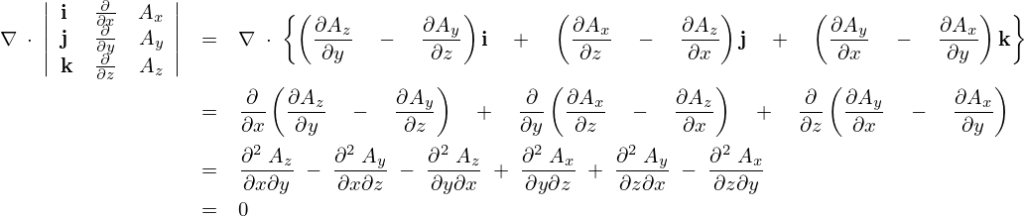
これにより以下のような条件が証明されます。
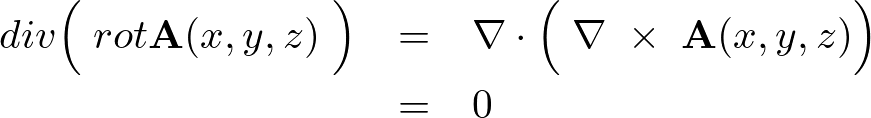

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
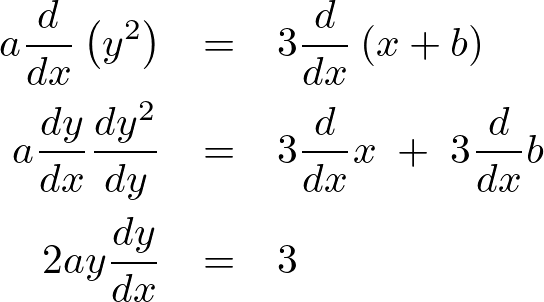
微分方程式いろいろTOPページLaTeXコード
カテゴリー
-
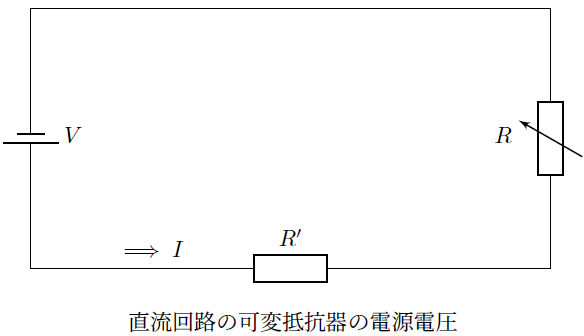
可変抵抗器の直列回路
カテゴリー
-
Cisco Packet Tracer
カテゴリー
-
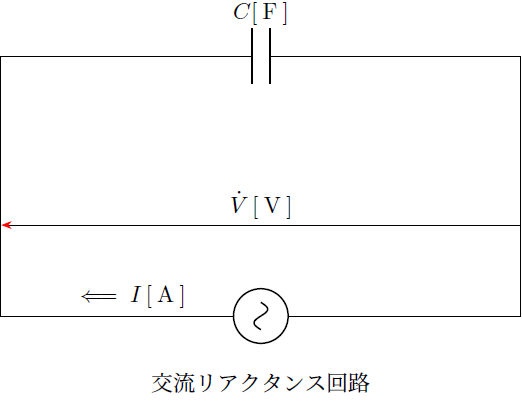
交流回路
カテゴリー
-
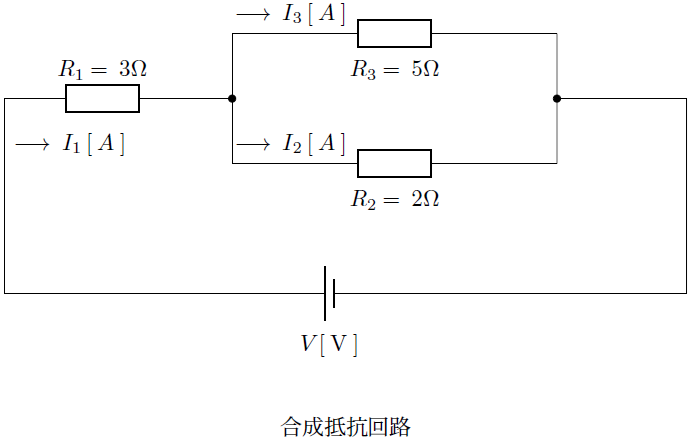
直流回路の合成抵抗
カテゴリー
-
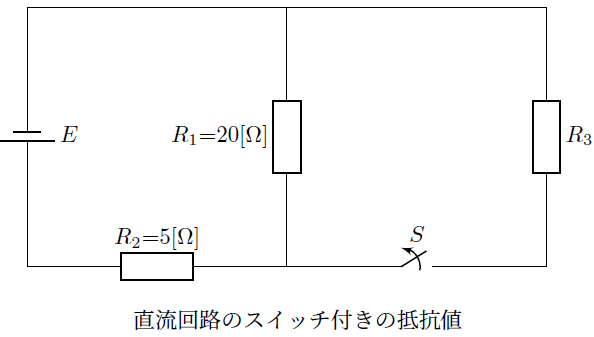
スイッチ付き回路素子の抵抗値
カテゴリー
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-