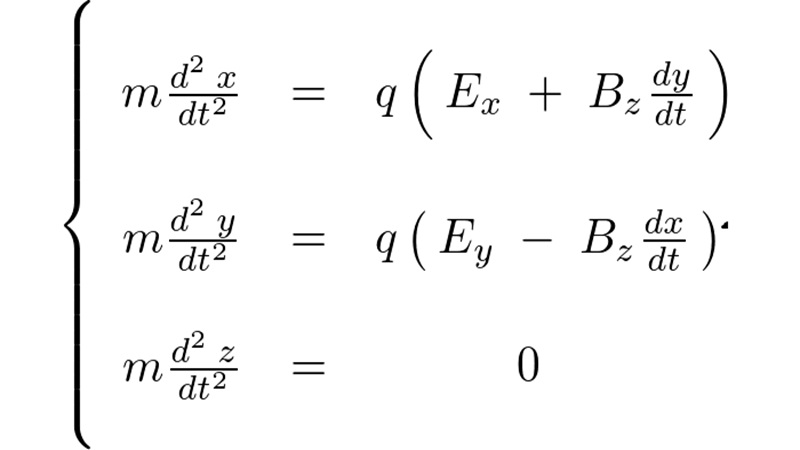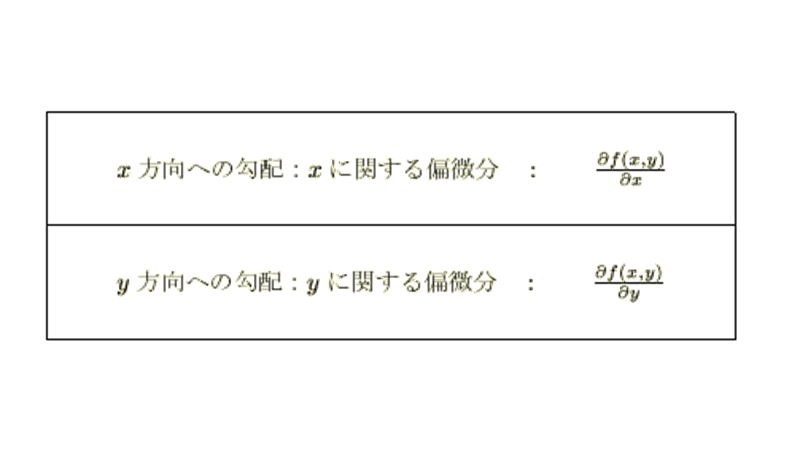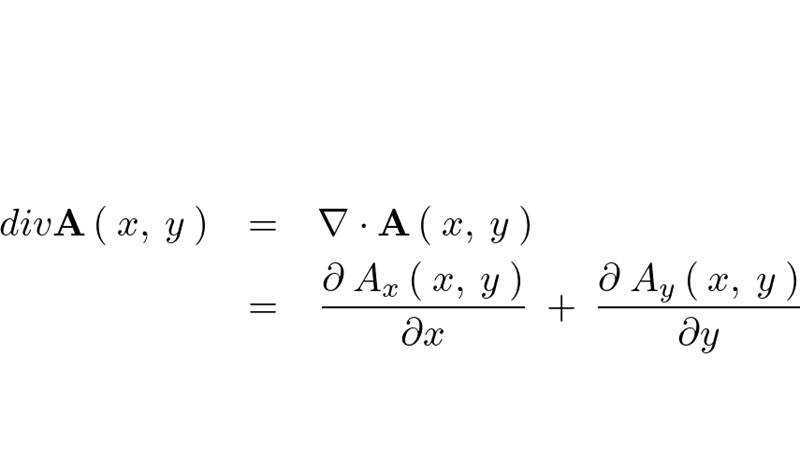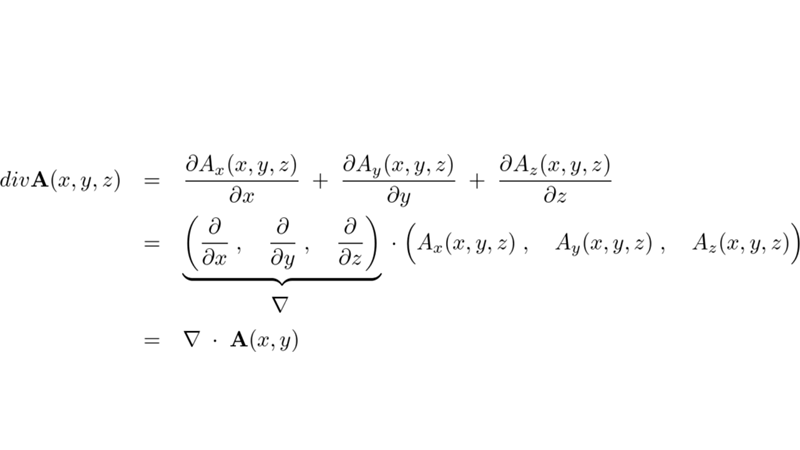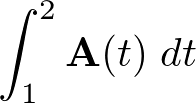【第０章】━ベクトルの概念

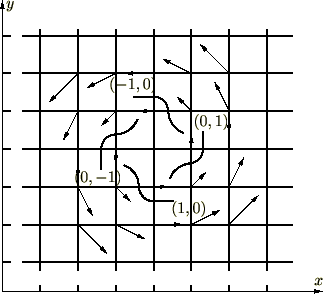
ベクトル解析とは、空間ベクトルを用いた一種の物理数学ともいえる分野であり、現代の物理学におけるさまざまな分野において活用されている極めて重要な理論的概念です。
特に電磁気学を理解するためには決して避けては通れない非常に重要な分野といえます。 しかしながら大学で習うベクトル解析というのは義務教育等で習う“ベクトル”とはだいぶ異なる形態を要しているので、初学者にとってとっつき難さを感じさせる部分が少なからずあります。

当サイトではこの部分をなるべく省き、わかりづらい表記や説明はなるべく避けながら数学の苦手な方でも理解できることを目的とし、さらにはビギナーにとって馴染みやすいように習熟させ、独学でこの分野における初歩的かつ基本的な内容を可及的速やかに理解かつ習得させるためのサポートを第一の目的としています。

ベクトルに関してのおさらい

“ベクトル”という概念は高校数学で習ったとおり、“方向”と、その“大きさ”をもった量です。

あるベクトルとベクトルがあったとします。これの合成を考えれば下図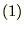より、ベクトルの始点からの終点を結んだベクトルの大きさです。

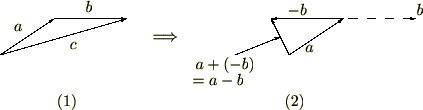
さらに上図より、ベクトルの差は和で表すことが出来ます。

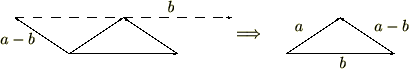
あるベクトルにおいて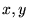方向の成分をそれぞれと書き、その軸、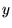軸の正の方向に対応した大きさがの単位ベクトルとすると、ベクトルは、

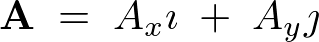
さらに、このベクトル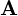の大きさを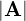とすれば、

零ベクトル

あるベクトルがあるとし、そのベクトルと大きさが同じでありながら向きが正反対のベクトルがあったとします。

それをとするならば、その加法を考えると、

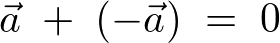
始点と終点が一致しているためにこのように表現できます。

これは向きを持つ線分とはいえませんので、これを大きさがの任意の向きを持つベクトルと考えと表します。

内積（ドットプロダクト）

2つのベクトル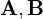があったとし、これの作る角がだったとします。

このとき、

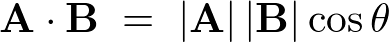
における左辺の部分を内積、またはドットプロダクトなどといったりします。

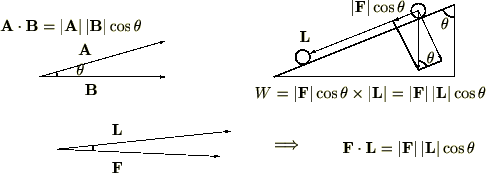
力の向きと変化ベクトルの方向が等しい時、コサインのをとすればよく、その場合には、

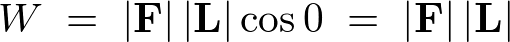
となります。

次に３次元の場合においての単位ベクターの内積を考えてみましょう。

同じ単位ベクトルの内積は、より、

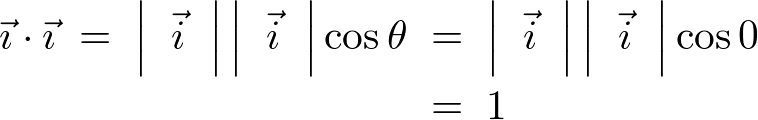
同様にして、

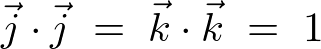
異なる単位ベクトルの内積は、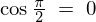より、

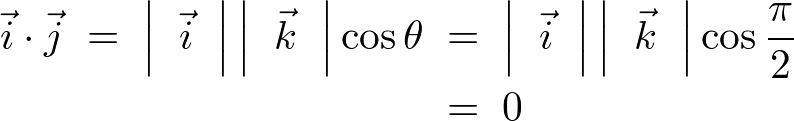
同様にして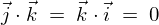となります。

外積（クロスプロダクト）

図のような垂直磁場の中に、電流が流れている長さの銅線を置くと、その銅線には下図右側に示すような方向に力（電磁力）が働きます。

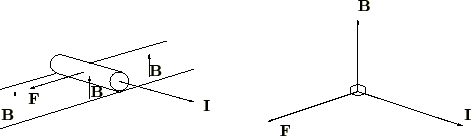
上図においては磁場と電流の方向は垂直になっています。

このときの電磁力の大きさは、

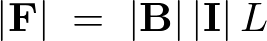
これらの“積”が、

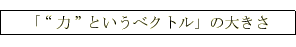
では、今度は磁場の向きと電流の向きが垂直ではない場合はどうなるでしょうか？

下の図のようにを角度だけ変えたとします。

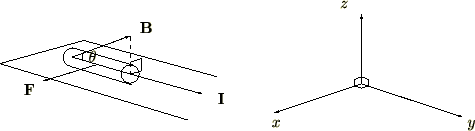
このようなとき、力の向きは同じですがの大きさが次のように変化します。

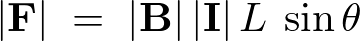
任意の向きの磁場中で電流の流れる長さの導線に働く力は、まとめると次のようになります。

大きさ
向き	向きとに垂直で、からへ回した右ネジの進む方向

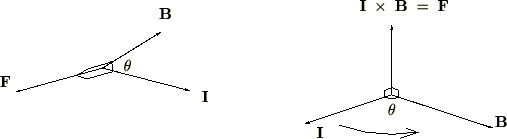
右ねじの進む向きとしているので、このことにより、

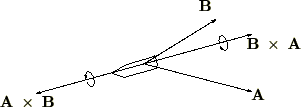
となります。

つまり、

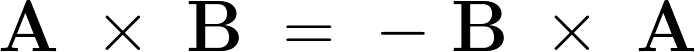
“外積は非可換である”ということが言えます。

このサイトの趣旨

• 閲覧対象者はおもに大学初年度の物理学科の学生を対称としていますが社会人や高校生などの一般の方に対しても、微分積分の簡単な知識があればあまり無理なく読み進めることが出来るかと思います。 内容は内積及び外積などの数学的一般化から、ベクトルの微分積分、さらにはスカラー場・ベクトル場などの数学的取り扱い、そしてベクトル場発散（ダイバージェンス）及びベクトル場回転（ローテーション）などの概念や計算法などとなっています。ページの進め方はプルダウンメニューから入る場合は左から右、上から下といった順序になっています。
• なお、外積及びローテーション（ＲＯＴ計算）における行列計算はサラス法によらない『行列式展開法』と呼ばれる計算法を提示してあります。 この計算法は実に単純かつ役に立つ計算法ですのであまり難しく考えずに軽い気持ちで学習していってください。また、ベクトル外積やローテーション（ＲＯＴ計算）などの３行３列の計算のみならず、それ以上の行列などの計算も何れ量子力学などの分野で必要になってきますので物理を志す方であるならばこの計算法は覚えておいて損はないことでしょう。
• 次の印刷用ページに第３章以降においてのベクトル勾配を作図するための表を作ってあります。グレースケール印刷などを指定してプリントアウトして使ってください。

◆リンクフリーです。こんなサイトでよかったら勝手にリンクしてください（＾ω＾）ﾌﾞﾋﾌﾞﾋﾌﾞｰ