重回帰分析とは（作成編集中）

単回帰分析の説明変数がひとつなのに対して説明変数が2個以上あるデータモデルを考え、推定量が下のような多次元のベクトル分布、

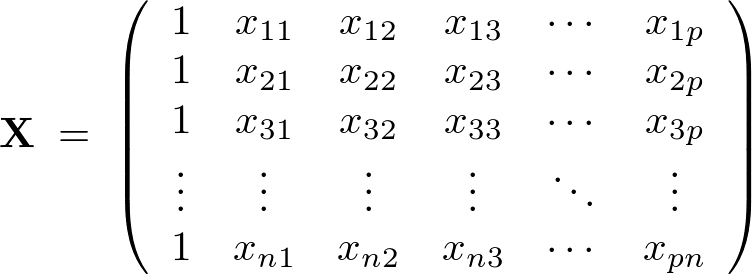
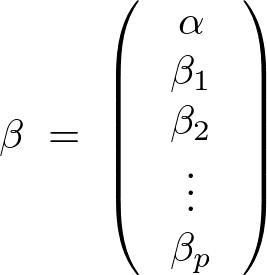
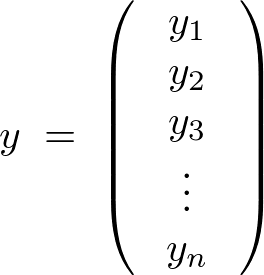
であるような説明変数、目的変数、回帰係数からなるデータ構造を考慮して次のようなデータモデルを考えます。

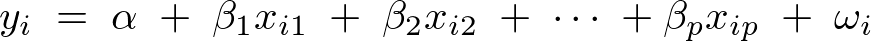
上記式の回帰直線におけるは切片を意味し、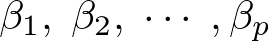は回帰係数になります。

データの表現

平均の表し方

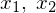の平均の表し方

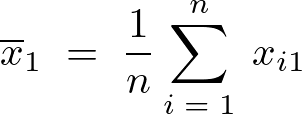
より、

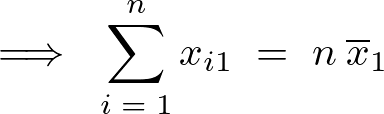
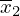に関しても同様にして、

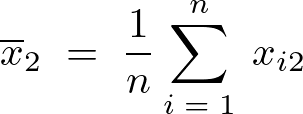
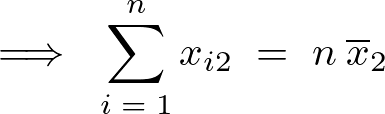
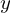の平均の表し方

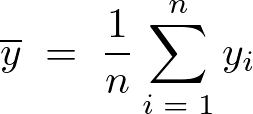
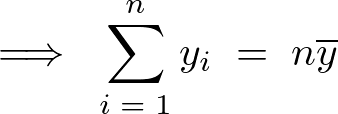
不偏分散

それぞれの不偏分散を次のように表現します。

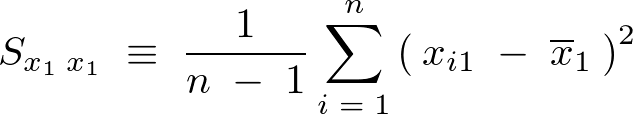
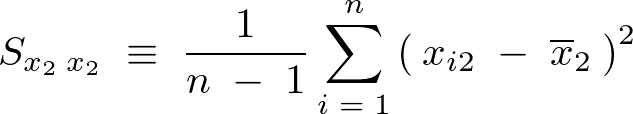
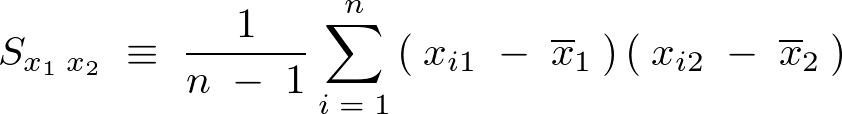
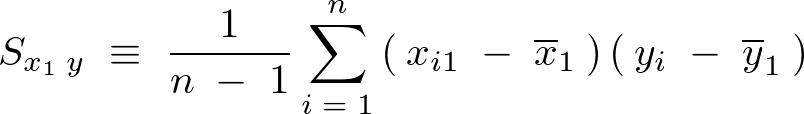
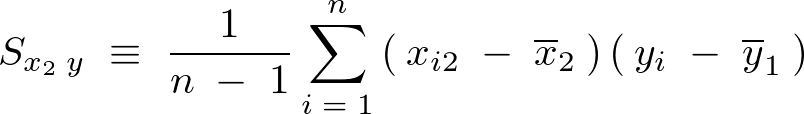
残差平方和という考え

切片であると傾き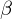の回帰直線を予測した式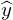の式と実際の観測値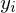との差を残差として次のように考えることにします。

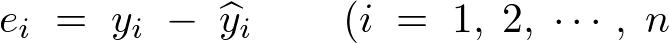
ハットは予測値や推定値を表す際に用いられるものになります。

残差平方和

そしてこれらのｎ個の観測値に対する残差の二乗和～残差平方和を次のように表すことにする。

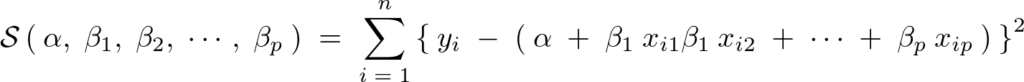
上記式において実際の観測値の差がなかった場合、つまり０であればこの残差平方和は0になると考える(ラグランジュ未定乗数法ということらしい)。

この残差平方和が可能な限り０（最小）になるような回帰係数群を求める方法を最小2乗法（LSM：least squares method）と呼ぶとのこと。

上記式においてそれぞれのパラメータであるα、βで偏微分しそれらを0と置いたものを採用していって正規方程式を導いていきます。

正規方程式の導出

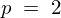とした場合

ここでは簡単のために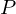を2つと置いた場合の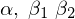をかを考えます。

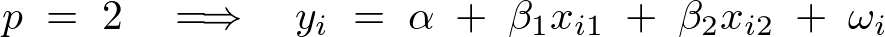
上記式における誤差の平方和は以下のように表せられます。

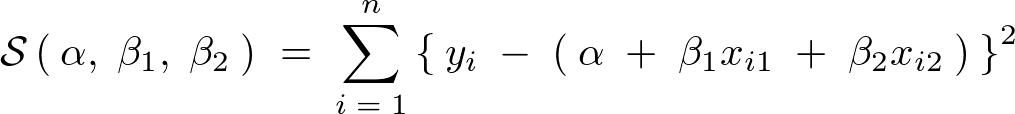
この上記式において左辺の、

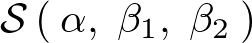
を回帰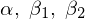に関して最小化することを考えるようにします。

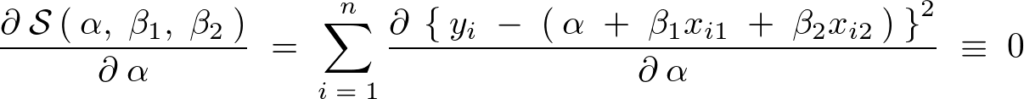
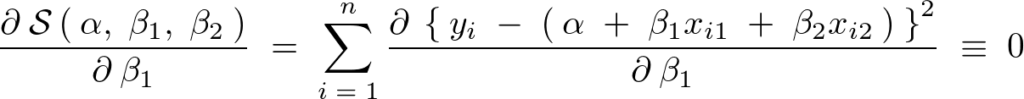
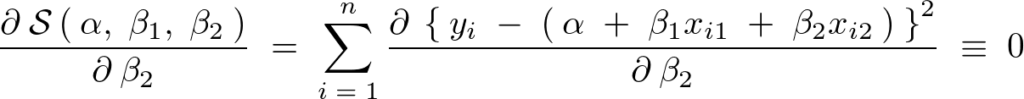
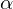による偏微分

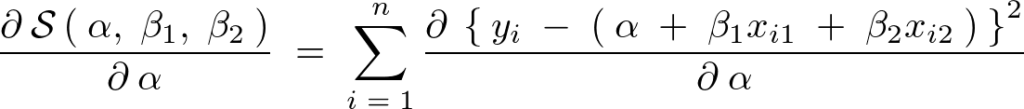
より、右辺をで偏微分していきます。以下のようにして連鎖律を適用します。

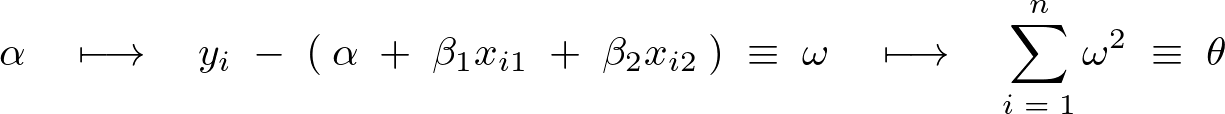
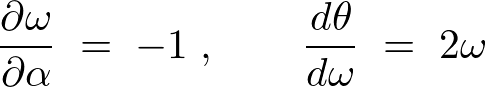
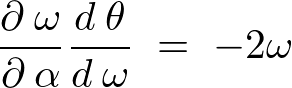
この結果より、による偏微分の結果は、

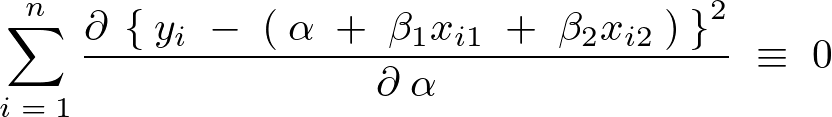
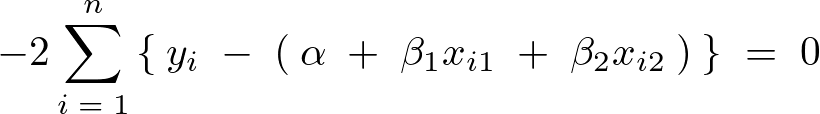
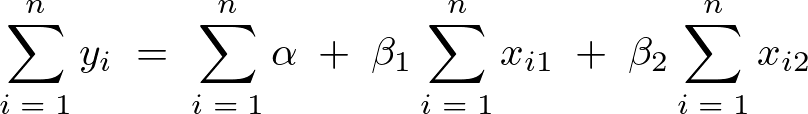
これらより、第一方程式は以下となります。

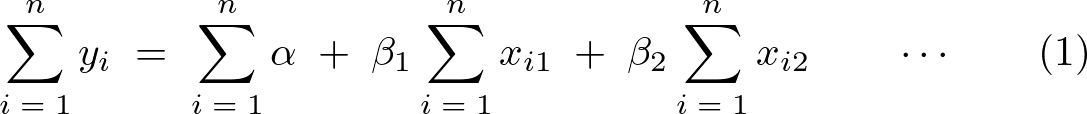
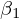の偏微分による第2方程式の導出

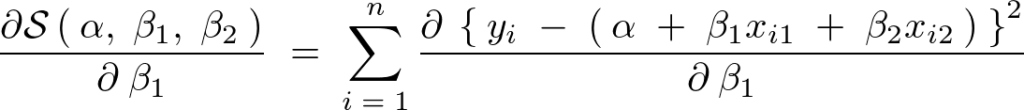
先ほどと同じように今度は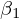で偏微分していきます。

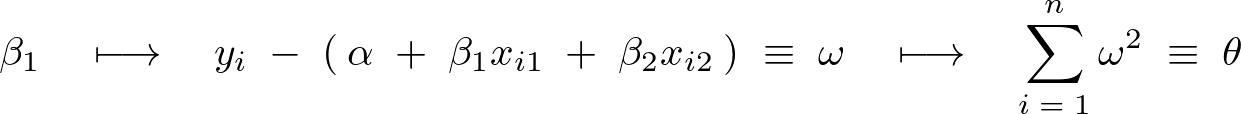
より、

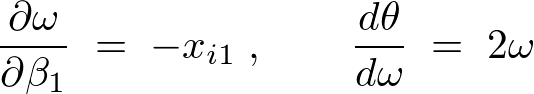
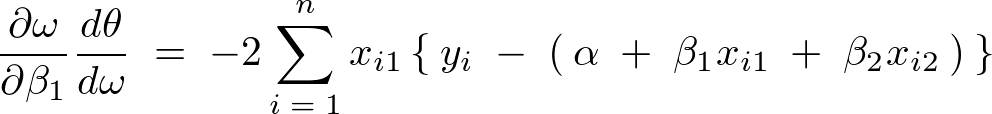
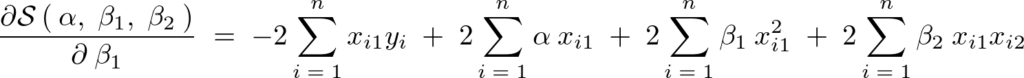
と出ますが、次のように、

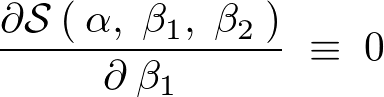
なので、

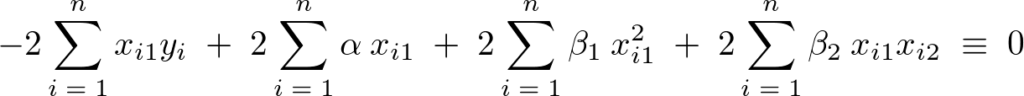
整理すると次のように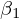に関しての第2正規方程式が求まります。

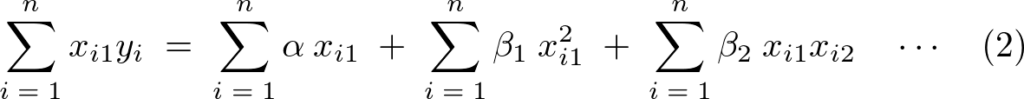
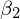の偏微分による第3正規方程式の導出

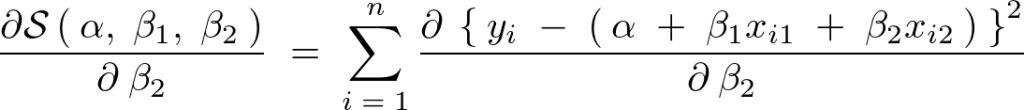
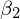の偏微分。

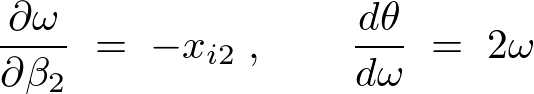
より、

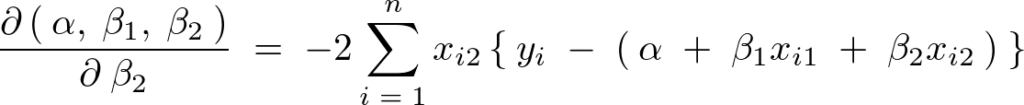
同じように最小となるように次のように置きます。

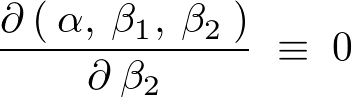
となるのでつぎのようにすると、

第3正規方程式が求まります。

これらによって以下のような3つの方程式が求まる。

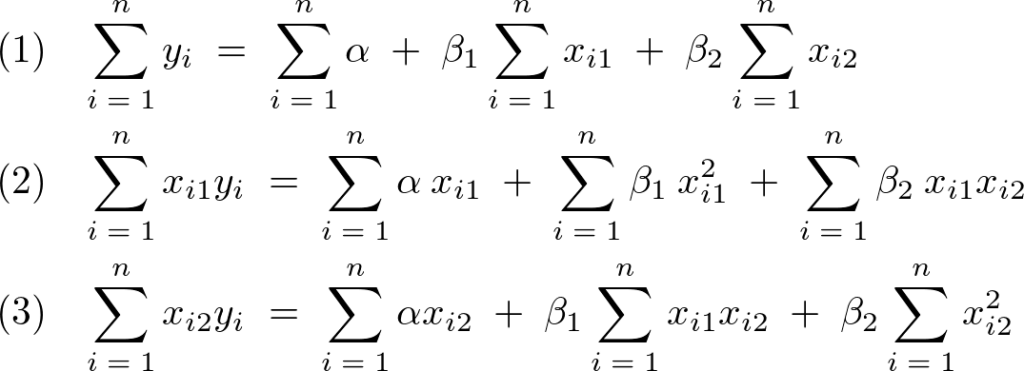
（１）式の変形

ここで先ほどの平均の変形式、

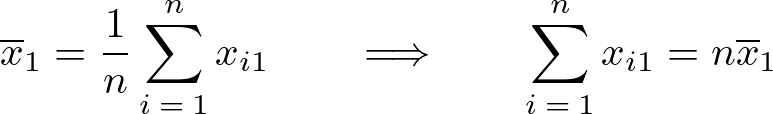
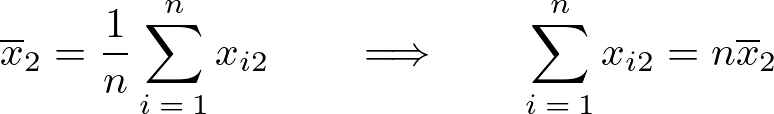
の式と上記（１）の式、

より、

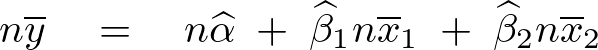
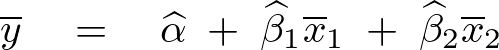
左辺右辺を移動させればまず最初にに関して次のような式が求まる。

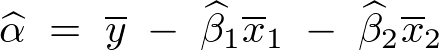
（２）式の変形

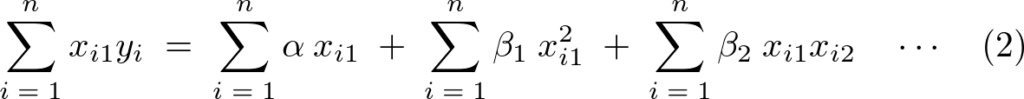
より先ほど求まったの式を代入して計算していく。

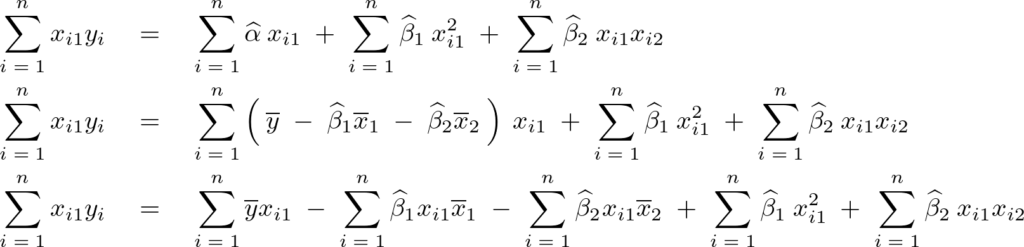
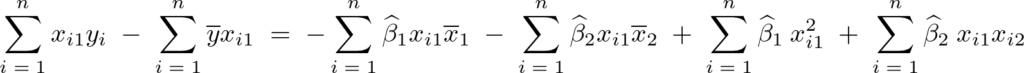
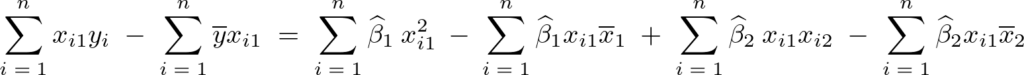
この結果により次のような第2正規方程式が求まります。

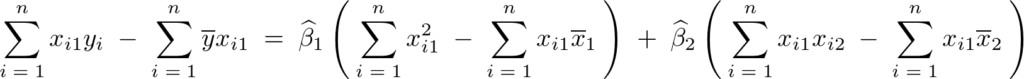
(3)式の変形

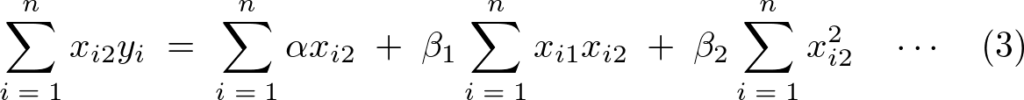
同様にに関しての式を上記第3方程式に代入していく。

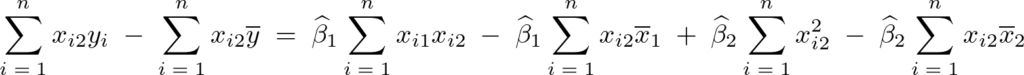
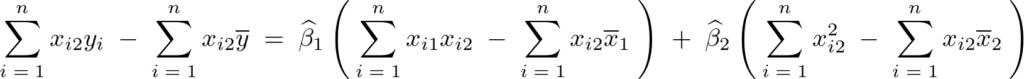
となるので第3方程式に関して次のように求まります。

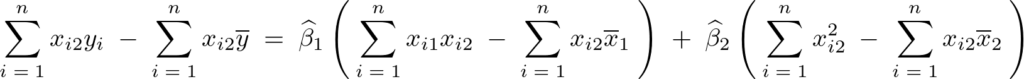
結果として以下のような3つの式が求まることになります。

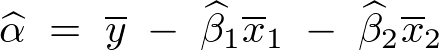
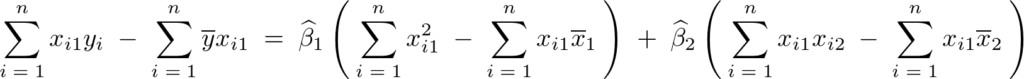
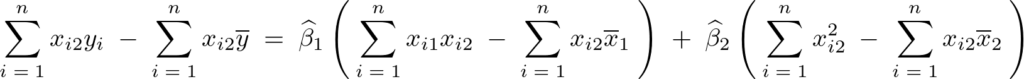
不偏分散式の変形

ここで不偏分散式などのデータ表現に関する一連の式の変形を考察します。
ひとまず平均は次のように表せられます。

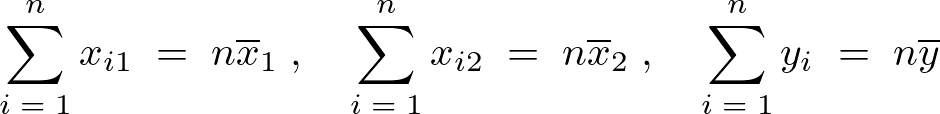
上記式を用いて不偏分散式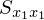を以下のように変形していきます。

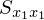式の変形

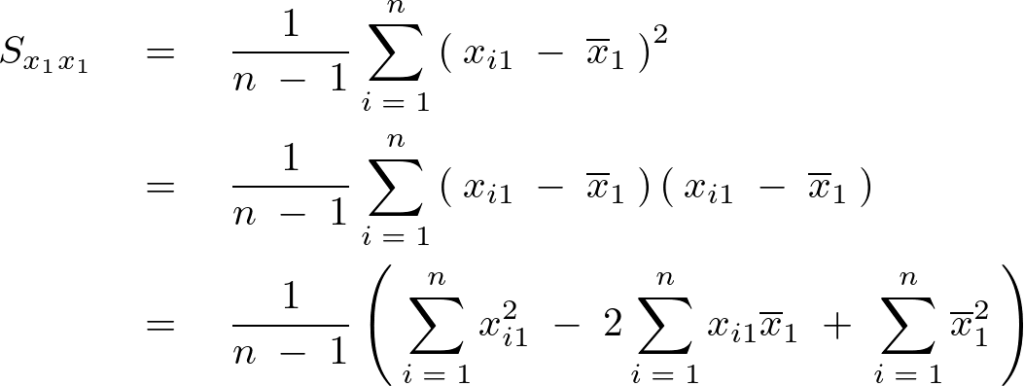
ここで先ほど変形した平均の式を代入していきます。

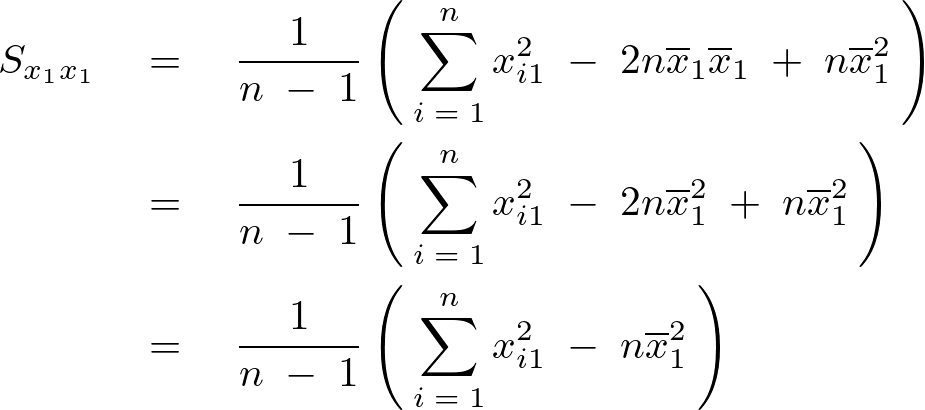
よってまず最初に次のような関係式が求まります。

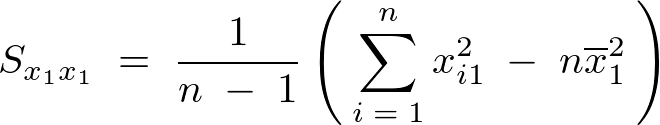
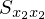式の変形

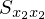の式の変形も次のように同様に行っていきます。

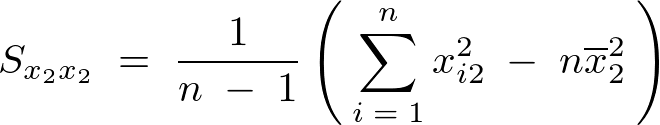
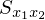式の変形

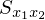の式変形過程

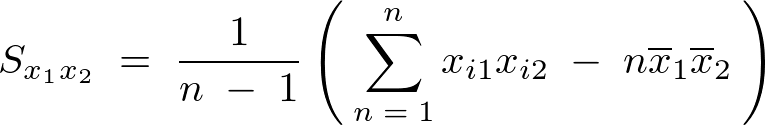
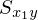式の変形

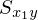式の変形過程

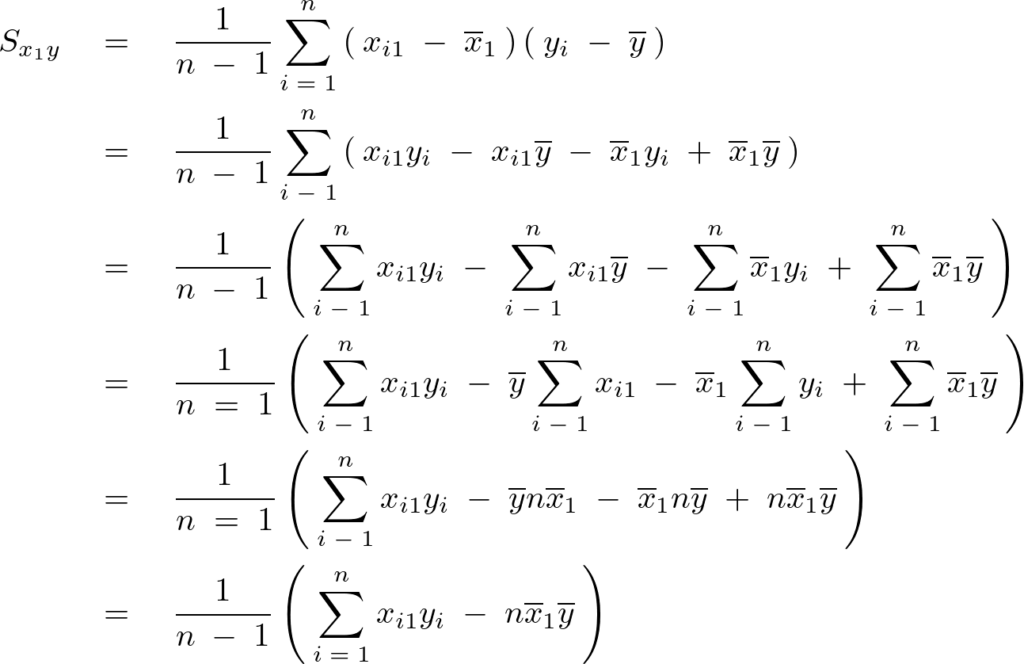
式の変形

式の変形過程

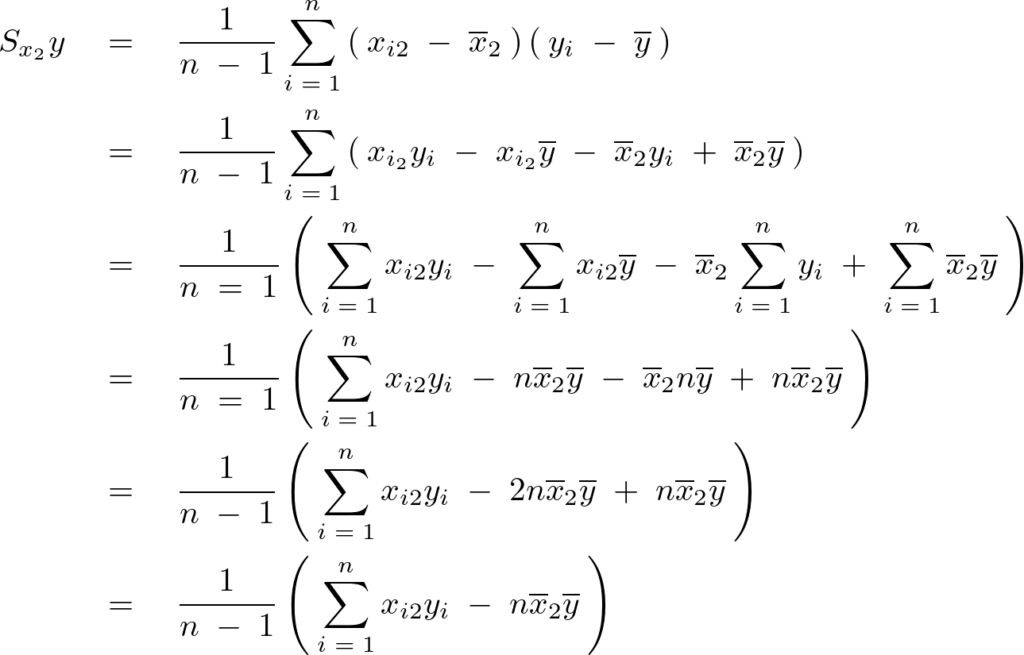
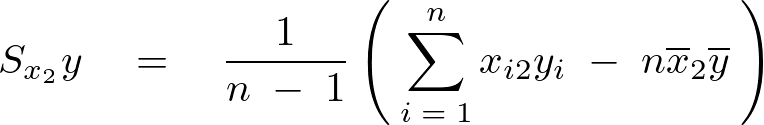
となるので以上、上記5つの不偏分散式はまとめると以下のように表現できることになります。

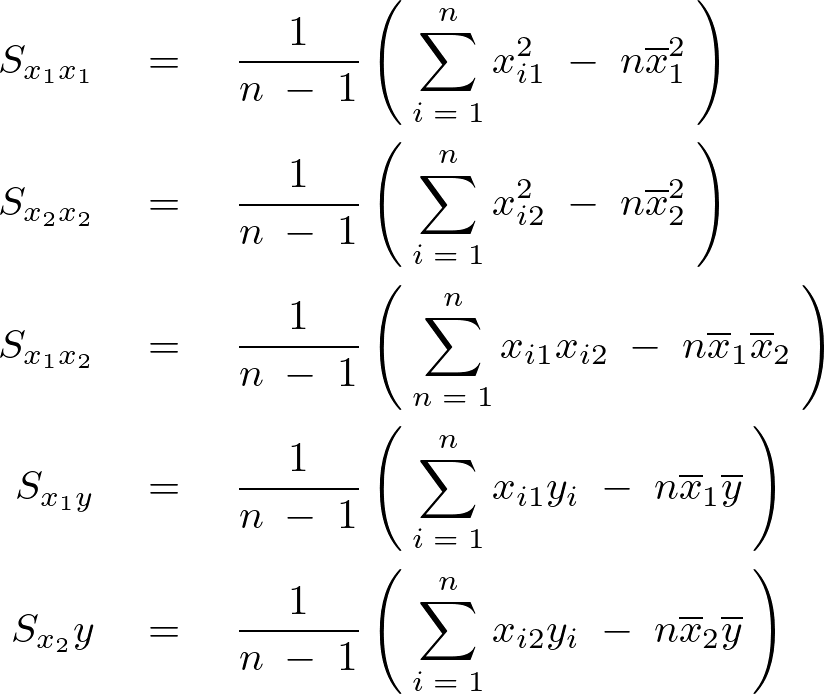
これらを当てはまると、先ほど求まった3式の正規方程式のうちの次の2つの正規方程式、

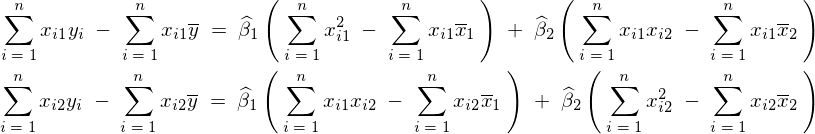
は、まず最初に先ほどの平均の式を当てはめれば次のように表現できることになります。

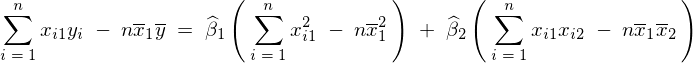
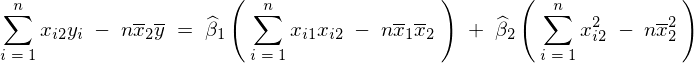
不偏分散式により、

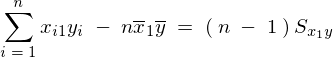
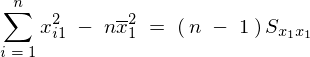
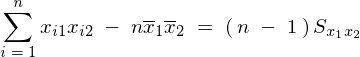
これらを第2方程式に代入すれば、

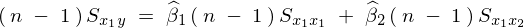
まず次のような関係式が求まります。