分散共分散行列とは
![]() 変量のデータから得られる行列における
変量のデータから得られる行列における![]() 個からなる対角成分の分散(
個からなる対角成分の分散(![]() )と
)と![]() 個の共分散(
個の共分散(![]() )を
)を![]() 次の正方行列にまとめたものになります。これについて考察していきます。
次の正方行列にまとめたものになります。これについて考察していきます。
ex.3変量の場合
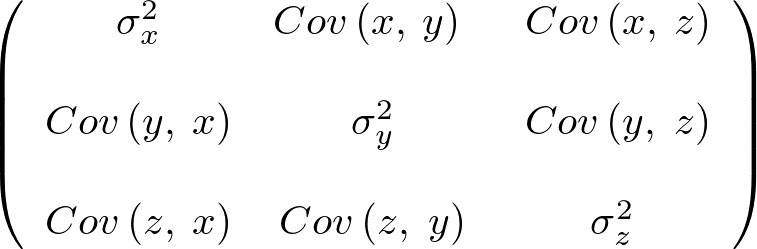
3変量正規分布に従う確率ベクトルの計算
![]() を次のような3変量正規分布に従う確率ベクトルとする。
を次のような3変量正規分布に従う確率ベクトルとする。
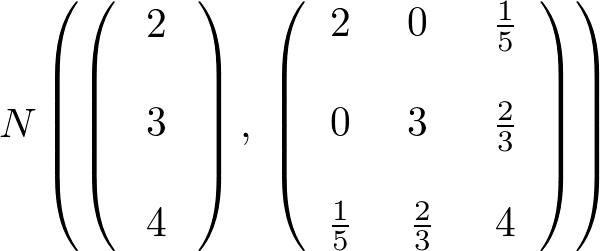
この時、次に示すベクトル、
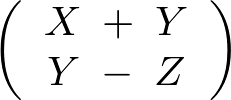
の分布における期待値ベクトルは、
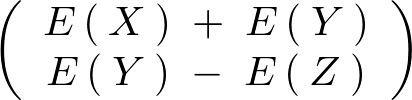
また、この多変量正規分布の分散共分散行列は、
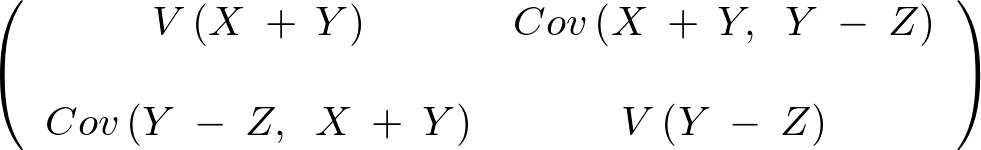
よって多変量正規分布の確率変数![]() が従う2変量正規分布は以下のようになる。
が従う2変量正規分布は以下のようになる。
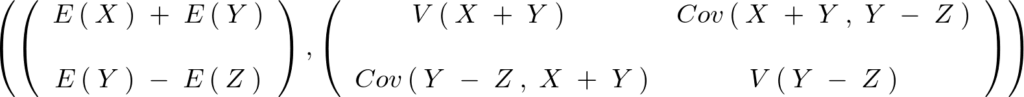
この上記行列における各要素を具体的に計算していく。
分散~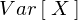
分散式における確認
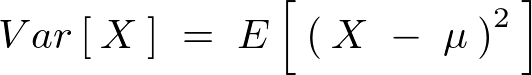
より括弧の中を計算していった場合次のようになる。
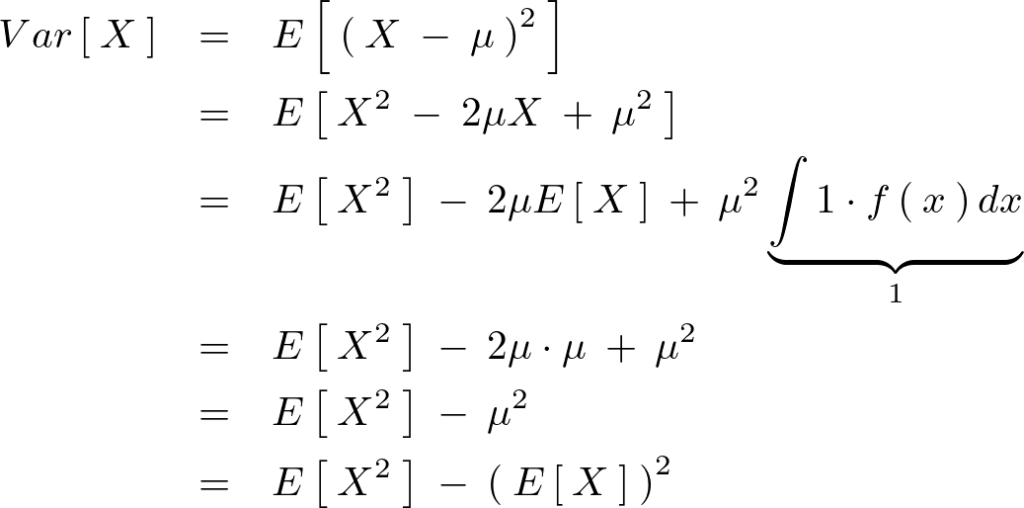
より、
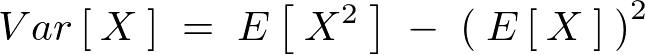
これをもとに先に示した2変量正規分布の対角成分における和の分散式と差の分散式を具体的に求めていく。
和の分散式
和における分散式は、
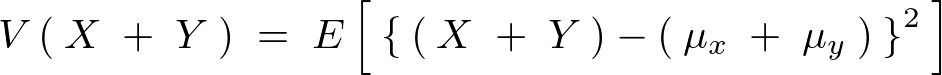
上記式を以下のように計算していく。
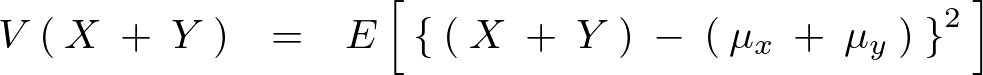
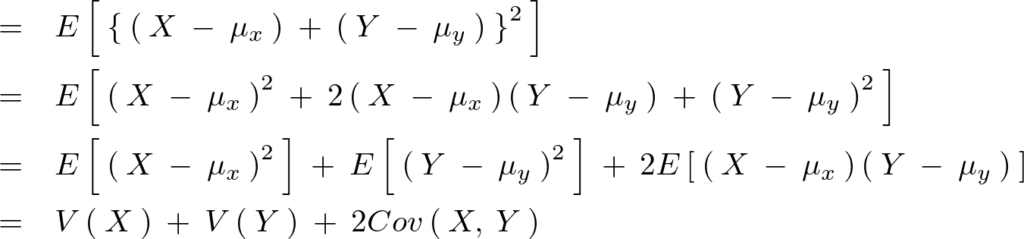
となるので結果として和の分散式に関して次のような関係式が求まる。
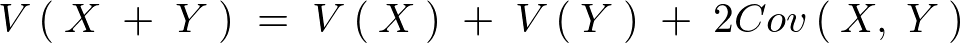
差の分散式
前述の式と同じように差における分散式は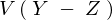 より、
より、
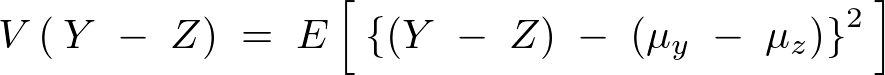
と表現できるのでこれを先ほどと同様にして計算していく。
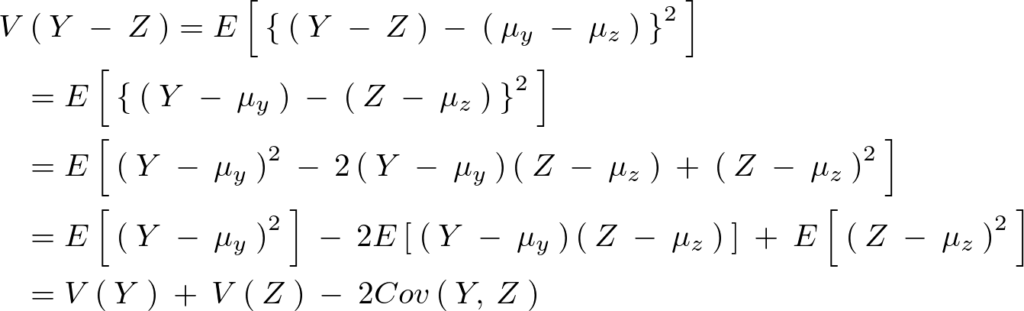
次のように求まる。
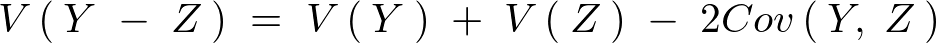
共分散~
次に分散共分散行列の対角成分以外の共分散の計算を行っていく。
式としては次のようになる。
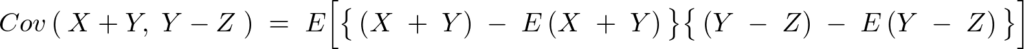
これを実際に計算していく。
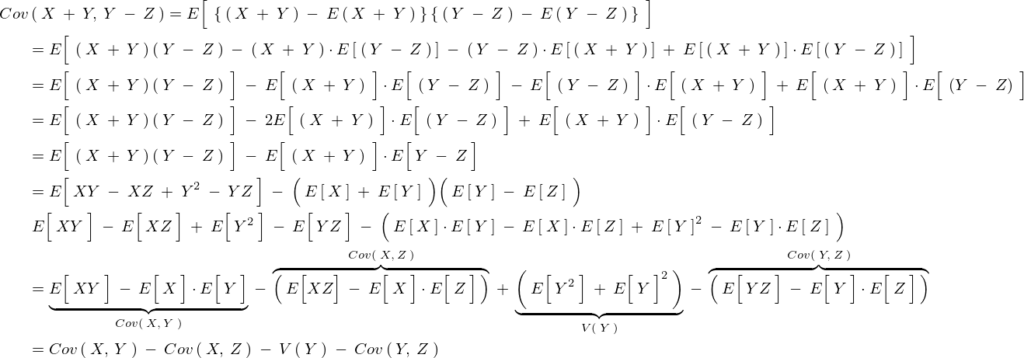
なお上記式変形においてEの中のそれぞれの変数は期待値の性質として定数であることを利用している。
結果次のように求まる。
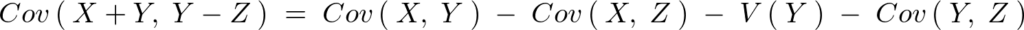
したがって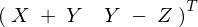 における多変量正規分布、
における多変量正規分布、
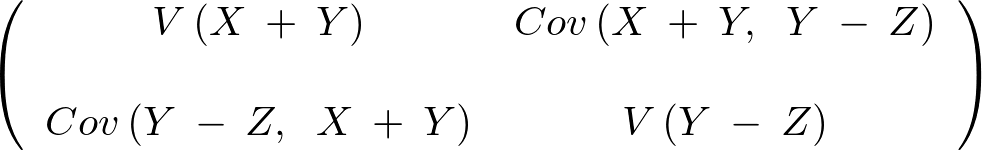
の分散共分散行列の部分は以下のようになる。
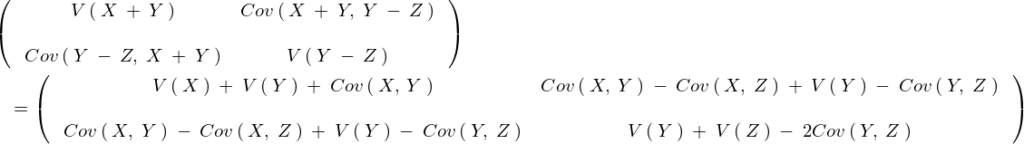
結果をまとめるとまず期待値に関しては、
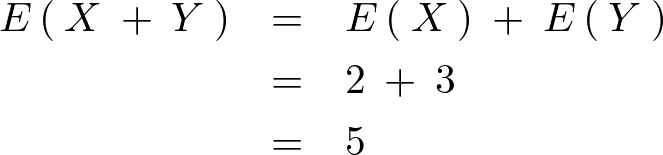
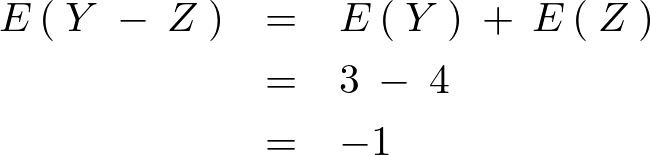
次に分散共分散行列の対角の分散成分、
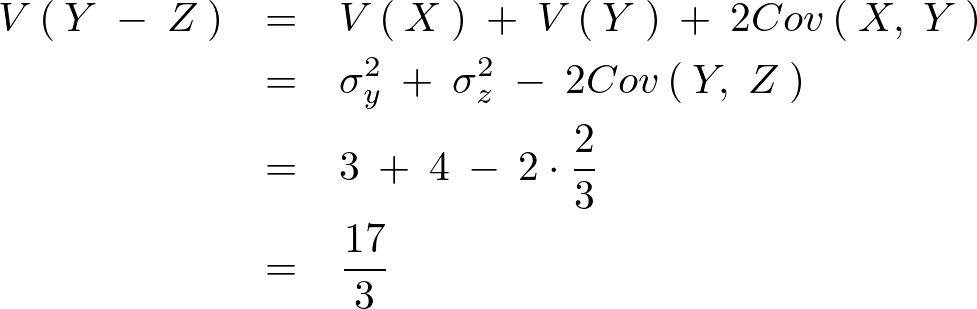
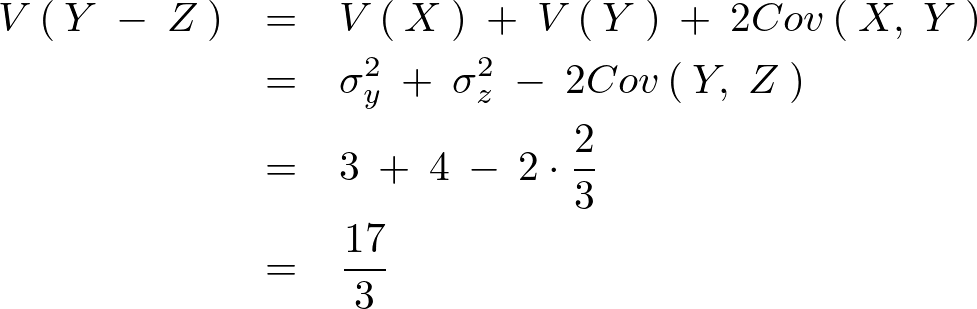
共分散は、
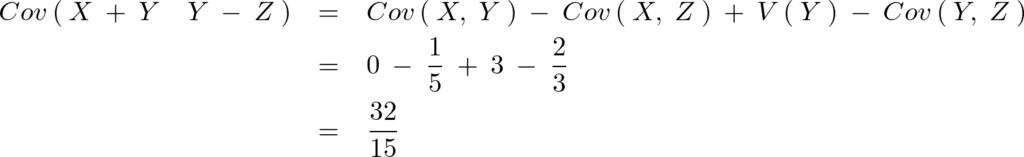
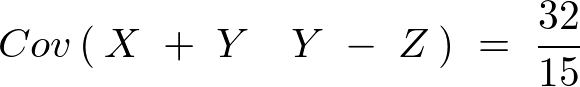
以上をまとめると、
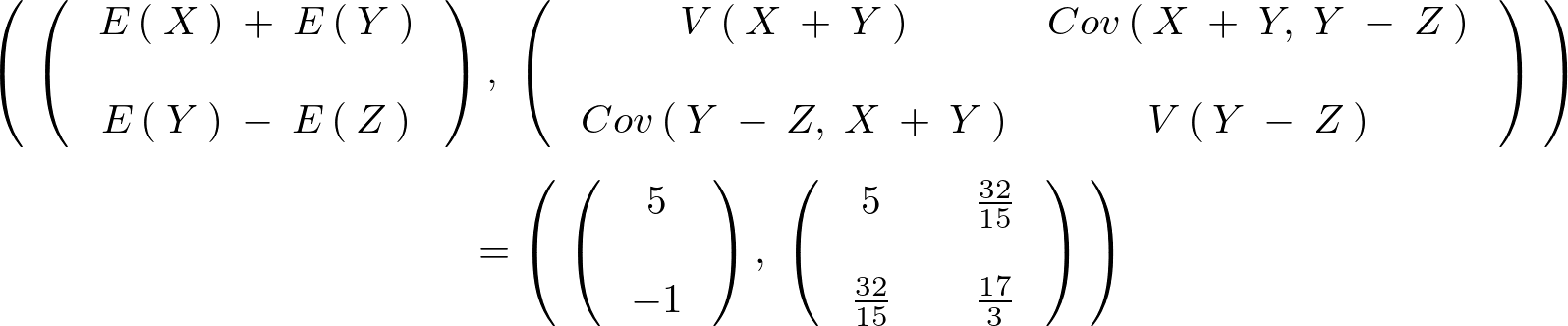


 の式を計算していきます。
の式を計算していきます。