RstudioでSIRモデル①
ケルマックマッケンドリック微分方程式
ケルマックマッケンドリック微分方程式(Kellogg-McKendrick differential equation)とは、人口動態や疫学において使われる微分方程式であり、この微分方程式は特定の条件下における人口動態をモデル化するために使用されるものになります。
以下のような3つの微分方程式よりなります。
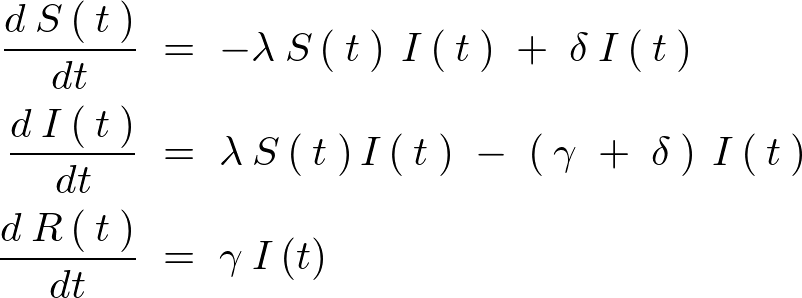
上記常微分方程式におけるそれぞれのパラメーター変数の意味は次のようになります。
| 罹患していない個体が感染症に罹患し、感染性の人口へ遷移する率 | |
| 感染性の個体が感受性人口へ戻る率 | |
| 感染性の個体が除外された集団へと戻る率 |
上記式において免疫を獲得しないで回復する率![]() を
を![]() と置いた場合の一連の微分方程式は以下のようになります。
と置いた場合の一連の微分方程式は以下のようになります。
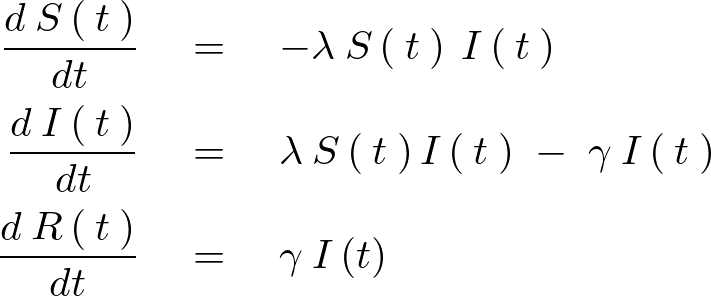
この上記式におけるそれぞれの集団が感染症に対して「感受性(Susceptible)」、「感染している(Infected)」、「回復(Recovered)」の3つの状態に分類されます。
| 感染症にかかるリスクがある集団 | |
| 現在感染している集団 | |
| 回復して再び感染するリスクがない集団 |
この変数![]() における常微分方程式を、ケルマックマッケンドリックのS-I-Rモデルと呼ぶらしいです。
における常微分方程式を、ケルマックマッケンドリックのS-I-Rモデルと呼ぶらしいです。
また人口を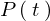 とすれば次のような関係式が成り立ちます。
とすれば次のような関係式が成り立ちます。
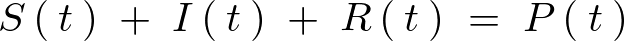
この微分方程式をRのパッケージのdeSolveを使って解いていきます。
RstudioによるSIRモデルの考察
一連の常微分方程式をRで解析していくためにはRのパッケージになるdeSolveを実装します。
deSolveをインストールしていない場合はinstall.package(deSolve)でインストールし、インストールが終わったらlibraryで読み込みして以下のように入力します。
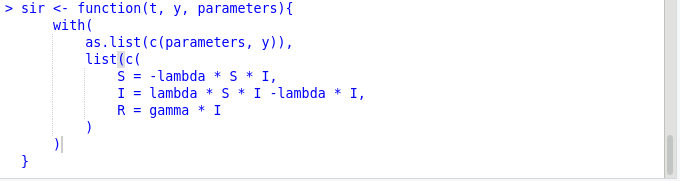
sir20201215 <- function(t, y, parameters){
with(
as.list(c(parameters, y)),
list(c
(S = -lambda * S * I,
I = lambda * S * I - gamma * I,
R = lambda * I)
)
)
}
次に以下のように入力します。
ちなみに代入している値は適当に考え出した数値(架空)なものなので本気にしないでください。
y_init <- c(S = 0.998537432, I = 0.000213768, R = 0.001248782)
deSolveをインストールしてライブラリ読み込みを行うと“ode”というのが使えるようになります。
以下のように入力してsir20201215のデータを今度はout20201215に入力します。
out20201215 <- ode(y = y_init, time = 1 : 120, func = sir20201215, parms = c(lambda = 0.995, gamma = 0.841305007))
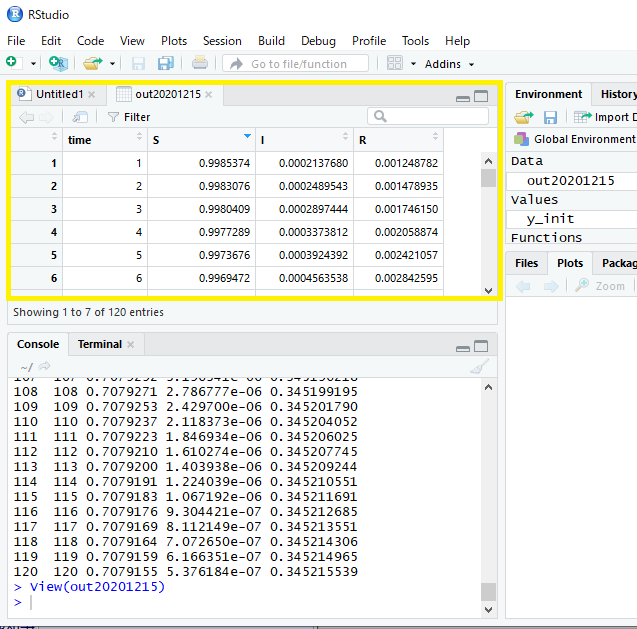
次のように入力して結果を表示させます。
View(out20201215)
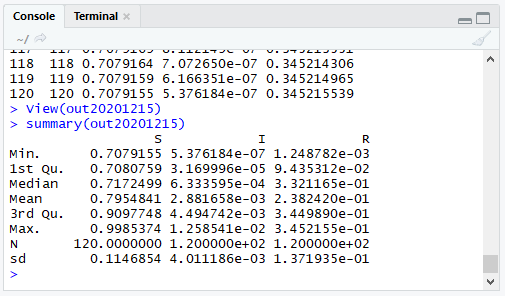
サマリーを表示させます。
summary(out20201215)
csvファイルの作成
write.csv(out20201215, "out20201215.csv")
作成されたcsvファイルをout20201215_dataへ格納します。
out20201215_data <- read.csv(file = "out20201215.csv", header = TRUE, sep = ",")
pairs(out20201215_data)
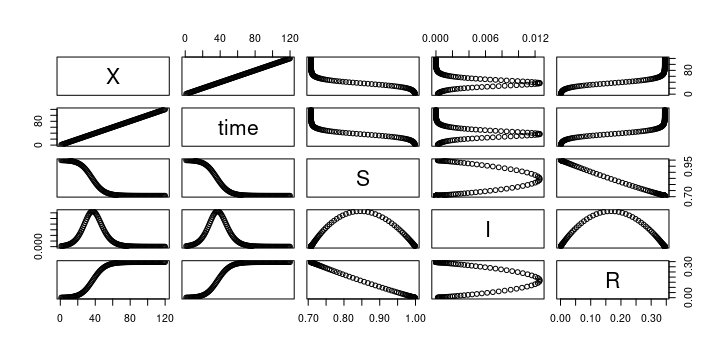
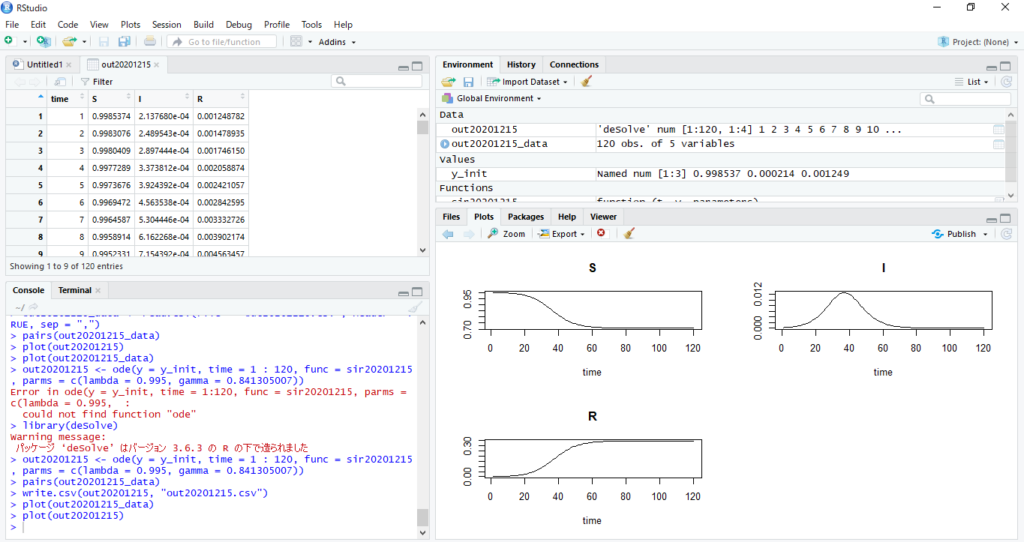
out20201215のデータの可視化
最後に以下のように入力して得られたS,I,Rのデータをグラフ化します。
plot(out20201215)
-
微分方程式いろいろTOPページLaTeXコード
続きを読む
-
可変抵抗器の直列回路
続きを読む
-
Cisco Packet Tracer
続きを読む
-
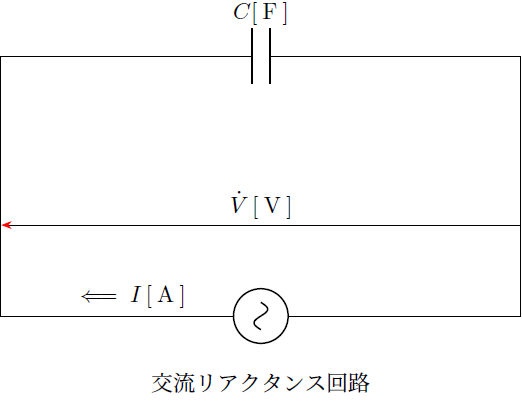
交流回路
続きを読む
-
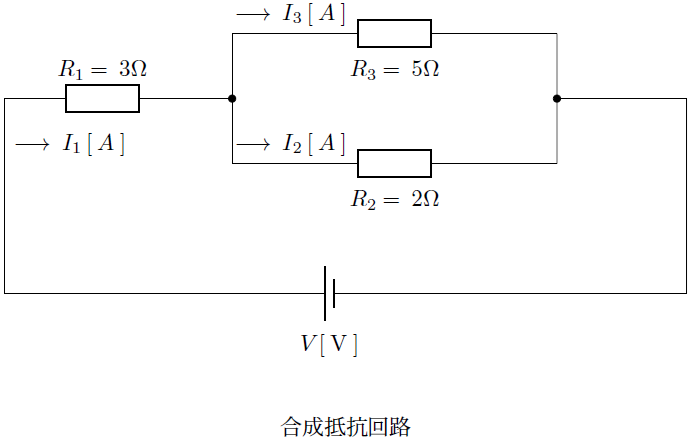
直流回路の合成抵抗
続きを読む
-
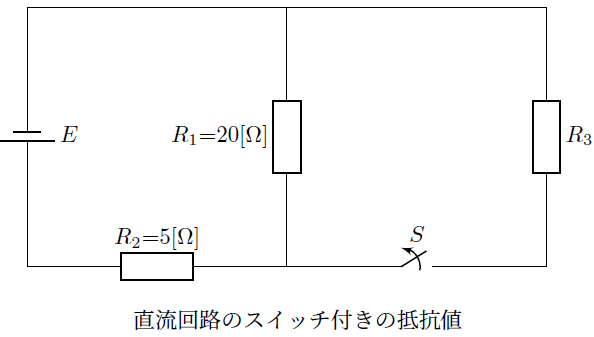
スイッチ付き回路素子の抵抗値
続きを読む
