円錐の慣性モーメントと平行軸の定理
平行軸定理を利用した円錐の慣性モーメントの求め方
前回にひき続き円錐に関する慣性モーメントを考察していきます。
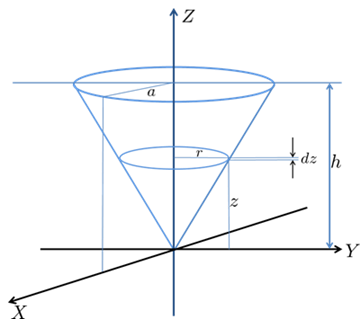
今回は平行軸の定理という物体(剛体)の物理的特性を利用しながら円錐の慣性モーメントを2つの視点から求め、また更に同じように平行軸定理を利用して円錐の重心周りの慣性モーメントを求めていきます。
平行軸の定理とは求められた慣性モーメントの軸とは平行な任意の個所に置ける軸周りに関する慣性モーメントを求める際に利用される定理になります。
このセクションを一通り学習すれば平行軸の定理に関してより理解が深まり、実は大変便利で役に立つ定理であることが理解できると思います。
平行軸の定理
平行軸の定理とは、剛体の重心を通る慣性モーメントに対し、その慣性モーメントの軸とは平行な任意の場所における軸周りに関する慣性モーメントを求める際に利用される定理になります。
式としては次のようになります。

上記式において左辺![]() が求めようとする任意の軸周りの(重心軸を通る慣性モーメントと平行な)慣性モーメント、右辺第1項が重心軸に関する慣性モーメントになり、第2項の
が求めようとする任意の軸周りの(重心軸を通る慣性モーメントと平行な)慣性モーメント、右辺第1項が重心軸に関する慣性モーメントになり、第2項の![]() が重心軸とは平行な軸までの距離、そして
が重心軸とは平行な軸までの距離、そして![]() が質量になります。
が質量になります。
今回の場合、上記の定理をそのまま適用するのではなく、この場合移動させる距離変数が微小円盤要素![]() の中に入っているので積分を実行する前の形において距離変数
の中に入っているので積分を実行する前の形において距離変数![]() を組み入れ、それで
を組み入れ、それで![]() で積分して目的の定理の第2項を導いていくことになります。
で積分して目的の定理の第2項を導いていくことになります。
回転軸が円盤の中心を通り円盤と平行な場合の慣性モーメントの計算過程
円錐における任意高さにおいて、その任意高さでの厚さ![]() の円盤の慣性モーメントを求めますがまず最初に回転軸が円盤の中心を通りその円盤と平行な場合の慣性モーメントの導出をします。
の円盤の慣性モーメントを求めますがまず最初に回転軸が円盤の中心を通りその円盤と平行な場合の慣性モーメントの導出をします。
円盤の慣性モーメントの導出

上記画像の円盤に関して、円盤の質量を![]() 、半径を
、半径を![]() とします。
とします。
また座標系は前回と同様にデカルト座標ではなく平面極座標のヤコビアンを使用して微小面積は![]() 、面積が
、面積が![]() なので、この円盤の密度
なので、この円盤の密度![]() は、
は、

さらにこの場合軸からの距離は、
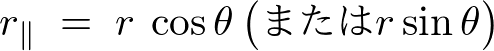
これらにより![]() は、
は、
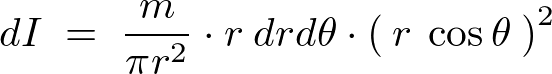
これを積分計算によって足し上げます。
なお途中の計算過程において三角関数の次のような公式を使用しています。
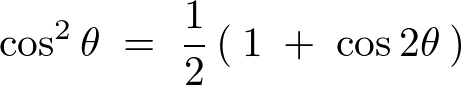
これを使って以下のように積分式を計算していきます(円盤の法線軸に関する慣性モーメントの積分計算過程)。

これにより円盤の重心を通り法線面と同一な方向軸に関する慣性モーメントは以下のようになります。

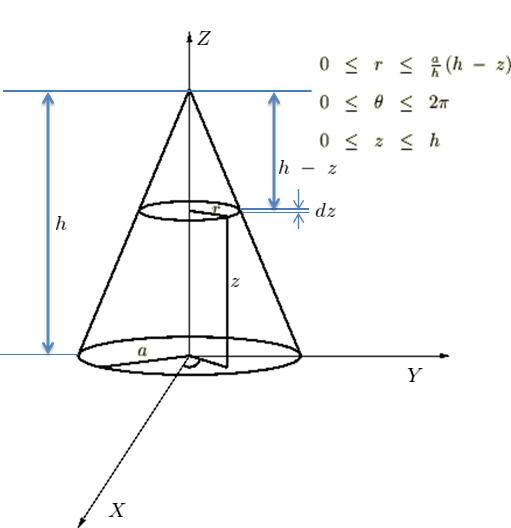
逆さ円錐の頂点周りに関する慣性モーメント
円錐内の任意の高さ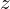 における
における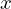 軸と平行な(頂点周りの)慣性モーメントの導出
軸と平行な(頂点周りの)慣性モーメントの導出


上記の円錐の高さ![]() におにおける
におにおける![]() に平行な軸に関する慣性モーメントを求めます。
に平行な軸に関する慣性モーメントを求めます。
まず最初に右のような円錐の高さに関する相似関係によって任意の高さ![]() における円盤の半径に関する距離変数
における円盤の半径に関する距離変数![]() を求めます。
を求めます。
![]() 軸に平行な任意の高さ
軸に平行な任意の高さ![]() にある重心を通る円盤面上の慣性モーメントを今仮に
にある重心を通る円盤面上の慣性モーメントを今仮に![]() 、その任意高さ
、その任意高さ![]() にある微小厚さ
にある微小厚さ![]() の円盤の質量を
の円盤の質量を![]() とします。
とします。
先ほど求めた円盤の重心を通り円盤と平行な軸に関する慣性モーメントは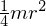
これにより微小厚さ![]() における重心を通り円盤面内と平行な慣性モーメント
における重心を通り円盤面内と平行な慣性モーメント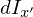 は以下のように置けることになります。
は以下のように置けることになります。

このとき![]() の質量は任意高さ
の質量は任意高さ![]() の円盤の面積が
の円盤の面積が![]() であり対象としている円盤の厚さが
であり対象としている円盤の厚さが![]() 、さらに円錐に関してはその体積と質量に関しては以下のようになります。
、さらに円錐に関してはその体積と質量に関しては以下のようになります。
| 円錐の体積 | 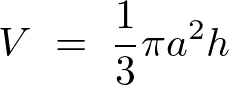 |
| 円錐の質量 | 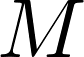 |
これにより円錐の体積密度は、
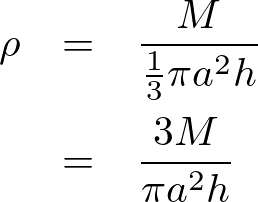
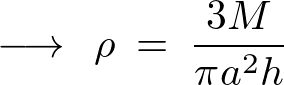
このときの![]() のしの質量はこの体積密度
のしの質量はこの体積密度![]() と円盤の面積、厚さ
と円盤の面積、厚さ![]() を使って以下のように表せられます。
を使って以下のように表せられます。
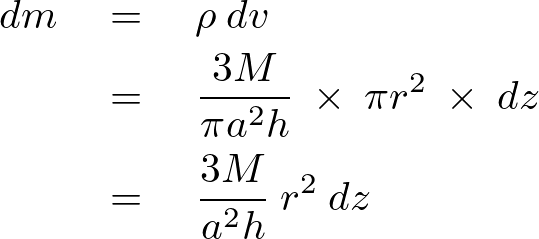
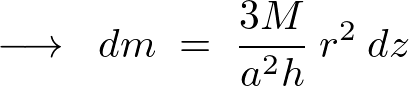
これらを先ほどの に代入していきます。
に代入していきます。
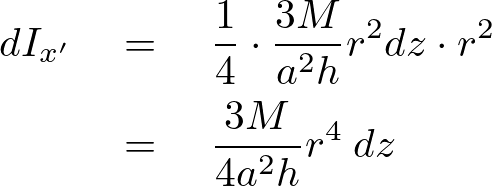
また先ほどの距離変数![]() に関して
に関して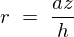 を代入してこれを積分によって足し上げていきます。
を代入してこれを積分によって足し上げていきます。

よって平行軸定理の第一項の逆さ円錐内の任意高さ![]() における質量
における質量![]() の重心を通る法線面内を通る軸に関する慣性モーメントは以下のように求まります。
の重心を通る法線面内を通る軸に関する慣性モーメントは以下のように求まります。

平行軸の定理における第2項の導出
重複しますが右辺第2項に関しては定理をそのまま適用するのではなく、この場合、移動させる距離変数が微小円盤要素![]() の中に入っているので積分する前の形を考えて距離変数
の中に入っているので積分する前の形を考えて距離変数![]() を組み入れます。
を組み入れます。
そこではじめて![]() で全体を積分して目的の定理の第2項を導いていくことになり、平行軸定理を紹介しているところでの式に関してかみ砕いて説明すれば以下のような状態から考察していくことになります。
で全体を積分して目的の定理の第2項を導いていくことになり、平行軸定理を紹介しているところでの式に関してかみ砕いて説明すれば以下のような状態から考察していくことになります。
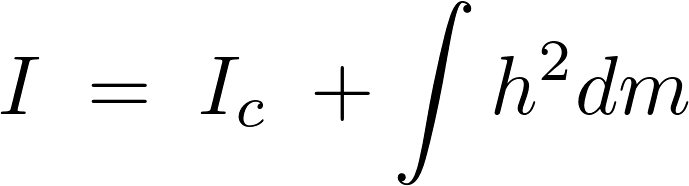
![]() 、およびその他は同じなので微小質量部分
、およびその他は同じなので微小質量部分![]() は同様にして、
は同様にして、
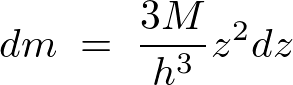
ここで求める平行軸定理の第2項を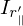 とおけば
とおけば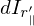 は、
は、

これを積分によって足し上げます。
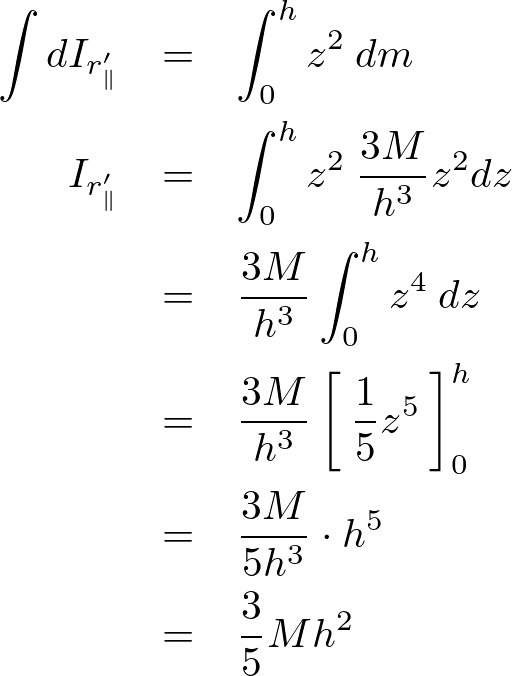
よって以下のように求まります。

求める円錐の頂点周りの慣性モーメントをここで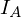 とおけば、
とおけば、
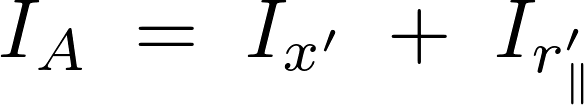
これらに代入していけば次のように求まります。
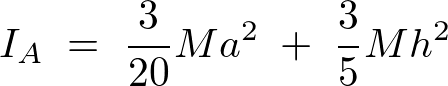
円錐の底面周りの慣性モーメント
任意の高さ![]() における円錐内の円盤の
における円錐内の円盤の 軸を通る円盤面内における慣性モーメントはすでに求まっていますがさらに視点を変えてあえて次のような座標における円錐の任意高さ中の円盤とみなした部分の慣性モーメントを求めていきます。
軸を通る円盤面内における慣性モーメントはすでに求まっていますがさらに視点を変えてあえて次のような座標における円錐の任意高さ中の円盤とみなした部分の慣性モーメントを求めていきます。
この座標における変数![]() に関しては次のような相似関係を持ちます。
に関しては次のような相似関係を持ちます。
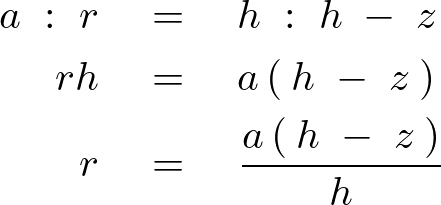
また先ほどと同じように体積密度、微小部分質量は、
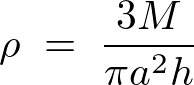
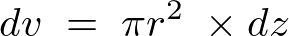
より同様にして微小円盤質量要素![]() は次のようになります。
は次のようになります。

となるので先ほど求めた微小質量要素は同様にして、
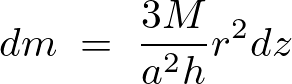
ここで先ほどの逆さ円錐に関して 軸に平行な任意の高さ
軸に平行な任意の高さ![]() の
の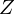 軸上を通る円盤面上の慣性モーメントの結果を
軸上を通る円盤面上の慣性モーメントの結果を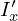 とおきましたが、結果的に同じ値になりますがひとまず区別をつけるために上記画像における任意の高さ
とおきましたが、結果的に同じ値になりますがひとまず区別をつけるために上記画像における任意の高さ![]() の位置での円盤の慣性モーメントを円盤面上の慣性モーメント
の位置での円盤の慣性モーメントを円盤面上の慣性モーメント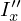 とおきます。
とおきます。
距離変数をrとして微小部分における慣性モーメント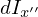 は、
は、
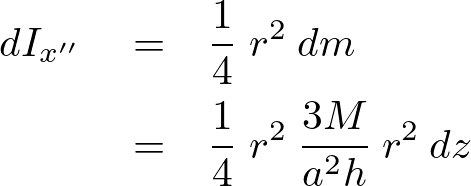
より、

これに距離変数rを代入していき積分計算していきます。

ここで前回の円錐における慣性モーメントの積分計算と同様に次のように置いて変数変換をします。
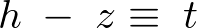
とおけば、
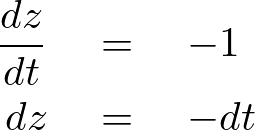
これにより積分範囲は次のように変更になります。
なので次のように計算していきます。

よって頂点周りにおける前段階の計算過程において出てきた円錐内の円盤に関しての慣性モーメントと同様に次のような計算結果が求まります。

さらに任意高さ の円錐における円盤面の法線に平行な慣性モーメント
の円錐における円盤面の法線に平行な慣性モーメント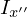 に対して平行で
に対して平行で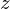 の距離だけ下方向へ移動した、円錐の底面における
の距離だけ下方向へ移動した、円錐の底面における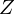 軸周りの慣性モーメントを
軸周りの慣性モーメントを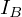 とおいて、その平行軸定理の第2項を
とおいて、その平行軸定理の第2項を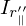 と置きます。
と置きます。
そうすると円錐中における円盤とみなした微小部分の慣性モーメント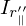 は平行軸の定理により、
は平行軸の定理により、
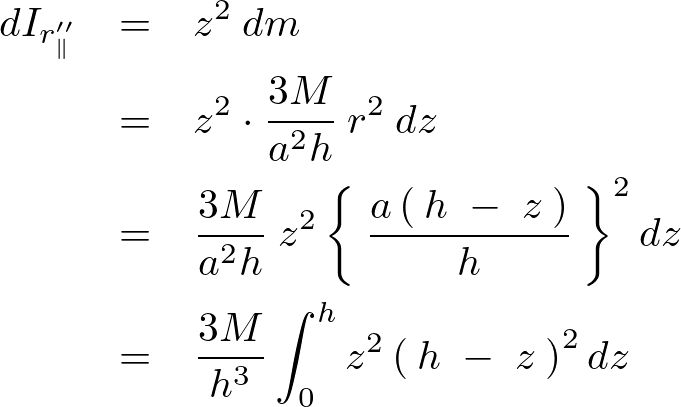
平行軸定理における第2項の移動変数の微小部分に関する慣性モーメント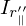 は以下のようになります。
は以下のようになります。

これを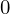 から
から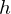 にわたって積分計算してきます。
にわたって積分計算してきます。

これにより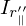 配下のように求まります。
配下のように求まります。

そうすると求める平行軸の定理を使用した円錐の底面周りのX軸に関する慣性モーメントは以下、

なので、これに代入すれば円錐の底面周りに関する慣性モーメントは以下のように求まります。

円錐の重心
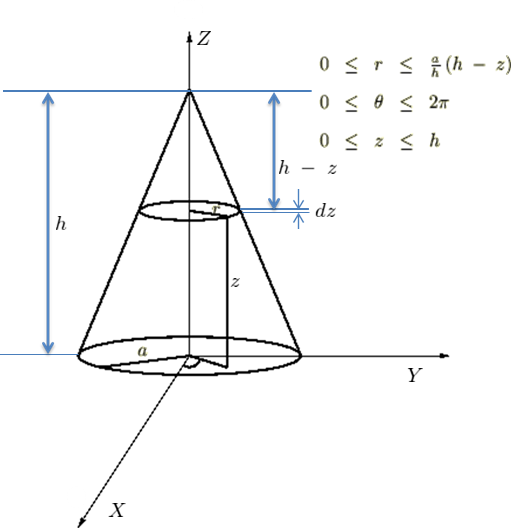
左の図を使って円錐の重心を計算していきます。
この画像の円錐は均一な質量で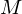 とし、高さが
とし、高さが![]() 、底面の半径が
、底面の半径が![]() のものと考えます。
のものと考えます。
円錐の体積は、
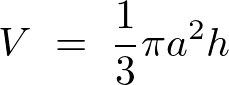
円錐の質量を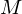 と置けば体積密度
と置けば体積密度![]() は、
は、
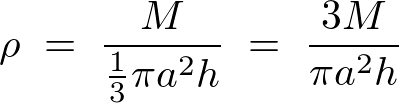
微小厚さの円盤の質量は先ほどと同じようにして、
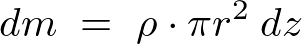
 軸上にあると考えられるので軸線
軸上にあると考えられるので軸線 軸上の任意の高さの位置を距離変数として、
軸上の任意の高さの位置を距離変数として、
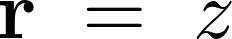
また距離変数![]() に関しては底面周りの慣性モーメントを求めた際のものを使用するので以下になります。
に関しては底面周りの慣性モーメントを求めた際のものを使用するので以下になります。
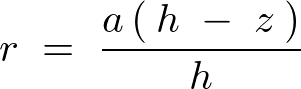
求める重心の値を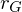 と置いて次のように計算していきます。
と置いて次のように計算していきます。
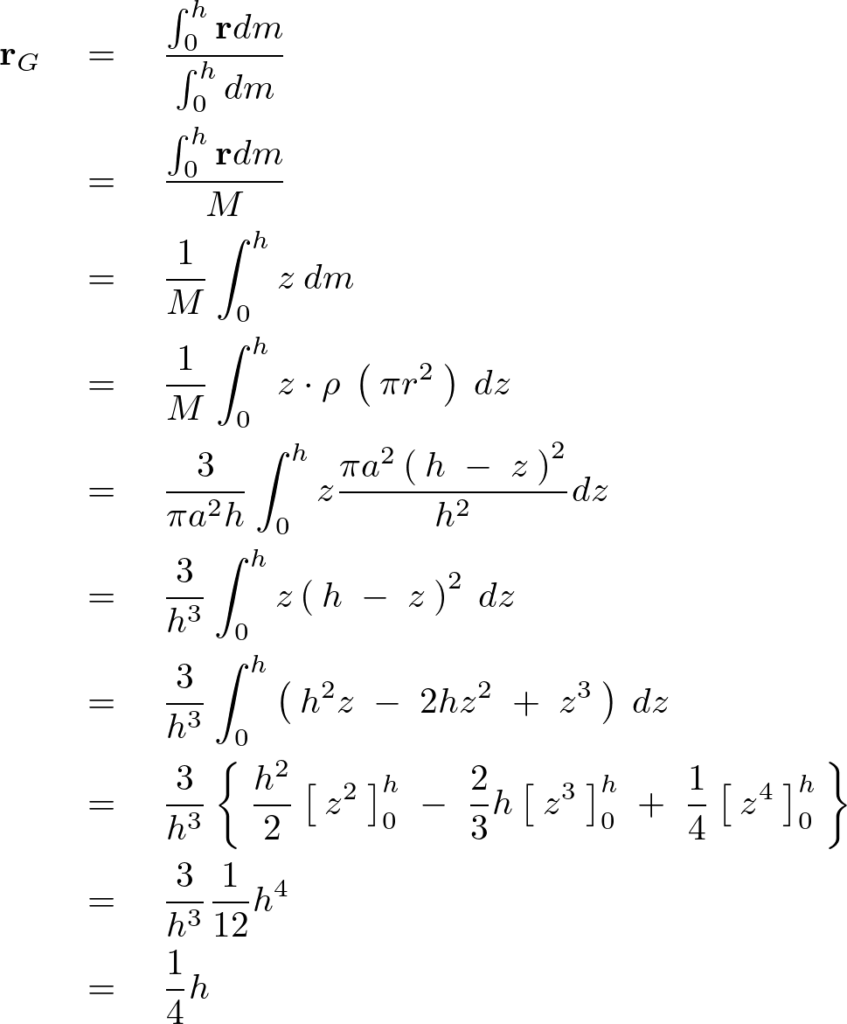
これにより円錐の重心は以下のようになります。
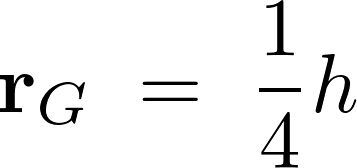
またこの結果によって円錐の頂点の位置からの重心までの距離は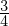 ということになります。
ということになります。
円錐の重心周りに関する慣性モーメントの導出

絵のようなクラッカー(円錐の物体)を考えたとき、その先っぽ(頂点)をもって上のほうにポーンと投げると、大体はクラッカー(円錐)の底面と平行にして、クラッカーの胴体部分あたり(重心)を中心にくるくる回るということが経験的にわかるかと思います。
この重心に関する慣性モーメントを平行軸の定理を使って求めていきます。
円錐に関しての重心周りの慣性モーメントの導出
円錐に関するそれぞれの頂点と底面周りに関する慣性モーメントの結果は次のようになりました。
頂点周りにおける円錐に関しての慣性モーメントの結果
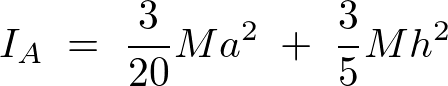
底辺周りにおける円錐に関しての慣性モーメントの結果
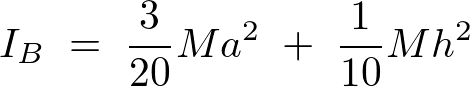
ここでさらに平行軸の定理を利用します。
この時、円錐の質量は定数の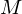 と決まっているので今までの距離変数を使用した前段階の積分計算は必要ありません。
と決まっているので今までの距離変数を使用した前段階の積分計算は必要ありません。
なので平行軸の定理をそのまま使用する(できる)ことになります。
頂点周りの慣性モーメント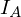 と、底面の中心心を通る法線面に平行な慣性モーメント
と、底面の中心心を通る法線面に平行な慣性モーメント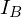 は、円錐の重心を通る底面に平行な軸に関する円錐の重心に関する慣性モーメントを
は、円錐の重心を通る底面に平行な軸に関する円錐の重心に関する慣性モーメントを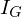 とおいた場合次のように表現できることになります。
とおいた場合次のように表現できることになります。
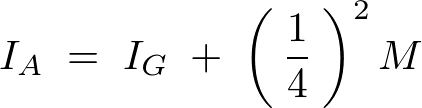

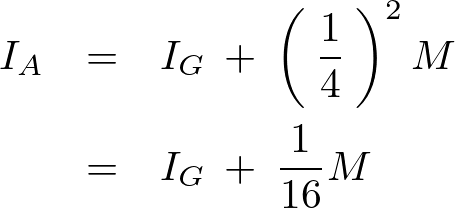

平行軸定理により、円錐の重心周りの慣性モーメント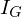 に関して次のようにな連立方程式が導かれます。
に関して次のようにな連立方程式が導かれます。


これらを一連の連立方程式ととらえて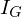 について計算していきます。
について計算していきます。
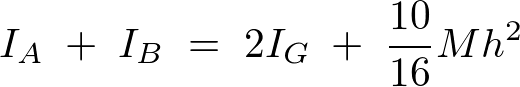
より、



よって以下のように求まります。
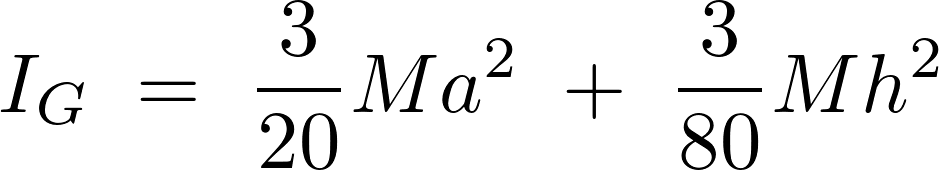
このように平行軸の定理というのは始めのうちは何かとややこしそうに思えますが一度きちんと理解し使えるようになれば便利で役に立つ定理であることがお分かりいただけたかと思います。
