円錐の中心軸を通る慣性モーメントの求め方
MoI of a Solid Cone
先日つべを見ていたところ、moment of ~というのが出ていたのでリンク先を見たら円錐の慣性モーメントの計算に関するものでした。
現在は削除されていますが、慣性モーメントに関するサイトを長い間運営しており円錐の体積の計算などのコンテンツを作っておきながら、なんで今までやってなかったんだ?という感じのコンテンツになるので今更ながら作成したものになります。
moment of inertiaとは
moment of inertiaとは慣性モーメントのことでこれは物体(剛体)の回転運動に関する物理的特性を示す用語になります。
サテライトサイトでこの慣性モーメント(よくわかる慣性モーメント)に関するサイトを運営しているので興味本位で見たところ結構面白かったので今回これの詳細な説明と計算過程をやってみたいと思います。
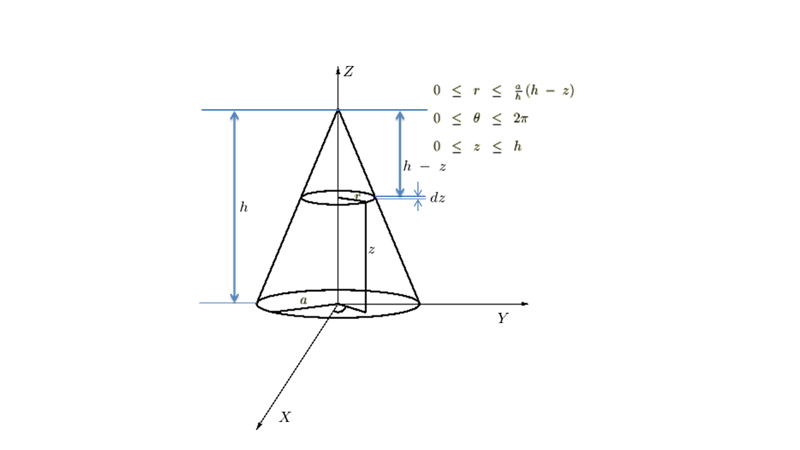
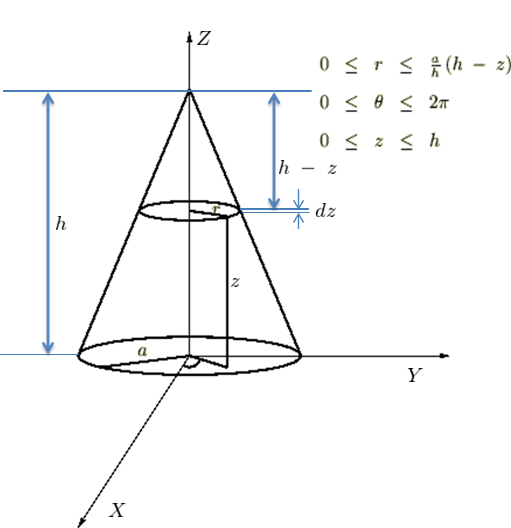
右の円錐の画像はもともとよくわかる慣性モーメントというサテライトサイトにて体積積分の例題として使っているものになります。
これを使って進めていこうと思います。
相似関係式は絵の通りの相似関係で進めていきます。
円錐の体積
円柱座標系における円錐の体積積分に関する計算過程
円錐の慣性モーメントを導出する前に円錐の体積を求めます。
円錐の体積を求める場合デカルト座標ではなく円柱座標に置けるヤコビアンを使用します。
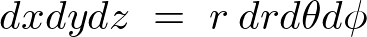
なお、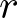 の範囲に関しては以下のような相似関係を利用します。
の範囲に関しては以下のような相似関係を利用します。
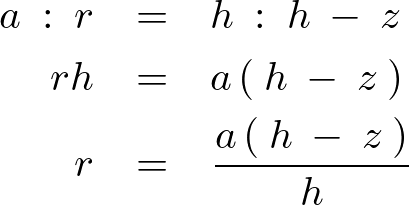
微小体積要素は、
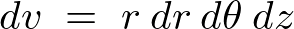
これらにより![]() に関しては先ほどの相似関係によって
に関しては先ほどの相似関係によって から
から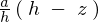 、
、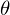 に関しては
に関しては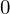 から
から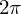 、
、![]() に関しては
に関しては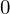 から
から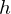 になるので体積積分における重積分式は以下のようになります。
になるので体積積分における重積分式は以下のようになります。
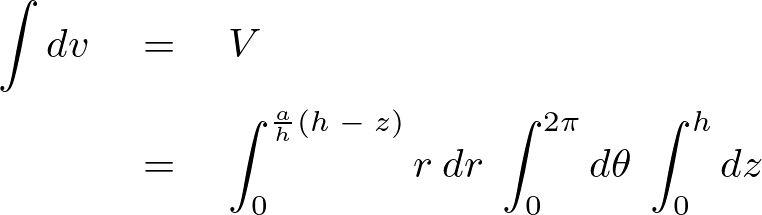
これを計算していきます。
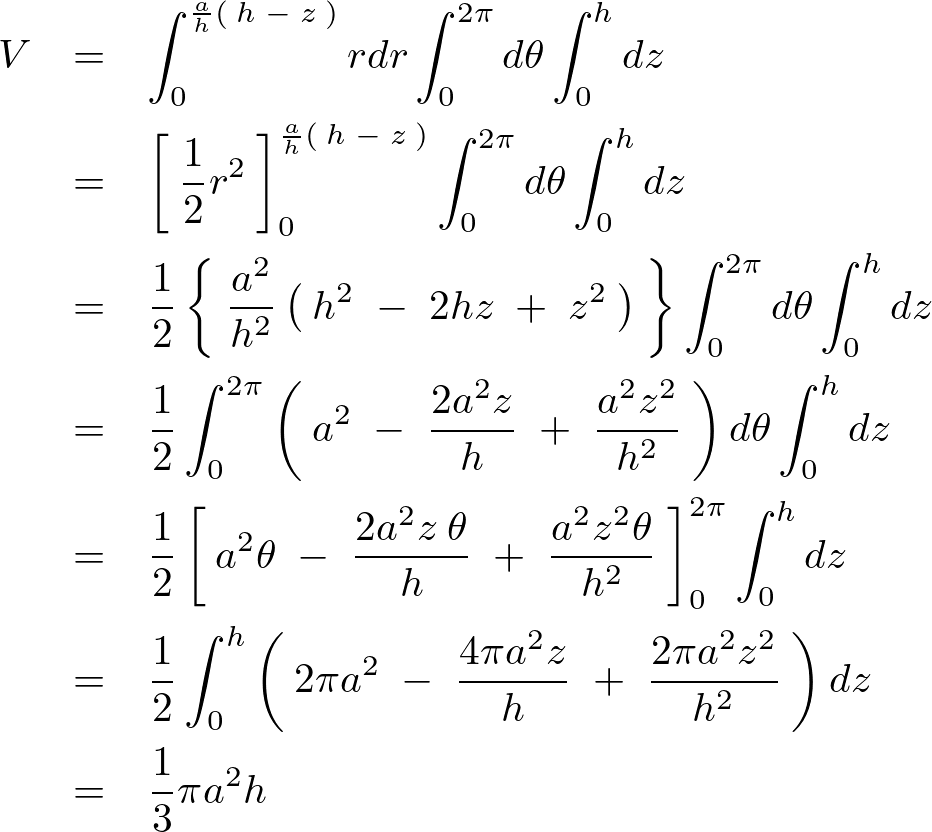
これにより円錐の体積は以下のように求まります。
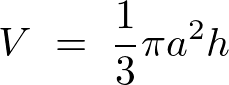
円盤の対称軸に関する慣性モーメントの計算
円錐の慣性モーメントを求める前にまず最初に以下に示す円盤の中心軸を通りその円盤対して垂直な![]() 軸周りの慣性モーメントを求めます。
軸周りの慣性モーメントを求めます。
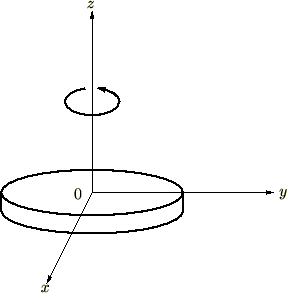
上記の画像の円盤は半径が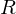 の円盤と考えてください。
の円盤と考えてください。
最初の円錐内の円盤の半径は![]() になっていますが、ここでの円盤の半径の長さは
になっていますが、ここでの円盤の半径の長さは とおいておき、半径の距離変数を
とおいておき、半径の距離変数を![]() としていますのでそこを注意してください。
としていますのでそこを注意してください。
座標系は2次元の平面極座標として考えれば、この時の微小部分の面積はヤコビアンによる計算結果により、
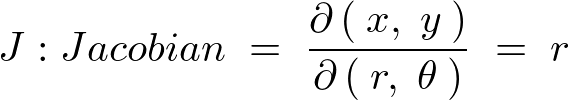
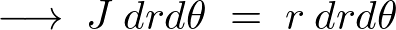
さらにこの円盤の全質量を今仮に![]() とし、面積は
とし、面積は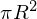 とすれば、円盤の密度
とすれば、円盤の密度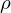 は、
は、
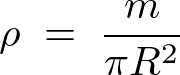
よって微小面積要素の質量は、
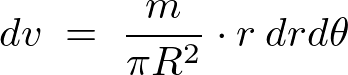
回転軸からの距離は、
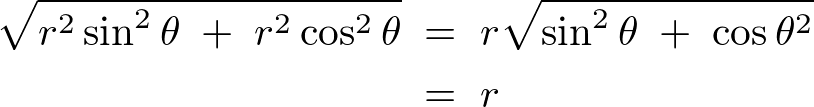
これらの結果により円盤の微小面積要素![]() は、
は、
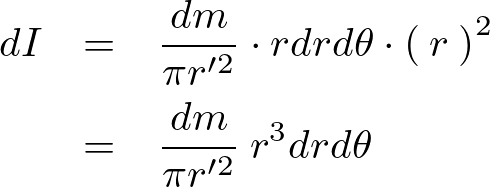
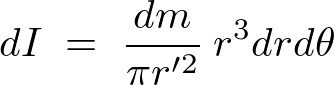
これを積分によって足し上げていきます。

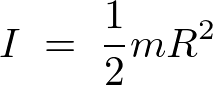
円錐の慣性モーメントの導出
材料がそろったのでここから具体的に円錐に関する慣性モーメントを計算していきます。
先ほど求めた円錐の体積と円錐の質量を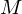 として円錐の体積密度を求めます。
として円錐の体積密度を求めます。
| 円錐の体積 | 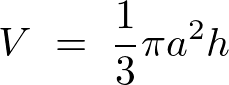 |
| 円錐の質量 |  |
これにより円錐の体積密度は、
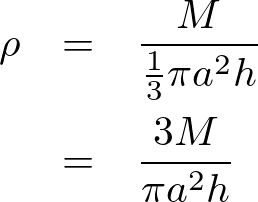
さらに上にある円錐の画像より任意の高さ![]() の位置にあると考える半径
の位置にあると考える半径![]() の円盤の微小部分の厚さを
の円盤の微小部分の厚さを![]() と考え、この任意の高さの微小円盤部分ととらえたところの質量を仮に
と考え、この任意の高さの微小円盤部分ととらえたところの質量を仮に![]() と置きます。
と置きます。
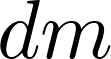 | 任意の高さ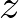 における厚さ における厚さ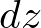 の円盤の質量 の円盤の質量 |
任意の高さ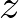 における円盤の半径 における円盤の半径 |
またさらに上記微小部分![]() に関しての質量は、
に関しての質量は、
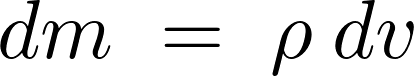
と考えられます。
この![]() に関してはさらに以下のように面積と厚さの掛け算と考えられます。
に関してはさらに以下のように面積と厚さの掛け算と考えられます。

これにより円錐の任意高さ![]() における微小厚さ
における微小厚さ![]() の質量は以下のように表現できることになります。
の質量は以下のように表現できることになります。
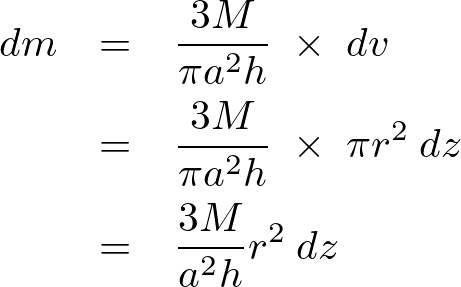
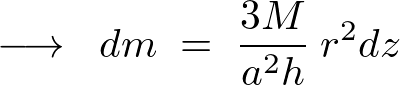
円盤に関しての![]() 軸周りの慣性モーメントに関しては、先ほど求めた
軸周りの慣性モーメントに関しては、先ほど求めた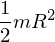 より、
より、![]() を
を![]() 、
、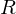 を
を![]() に対応させて考え、さらに
に対応させて考え、さらに![]() 軸周りの慣性モーメントを
軸周りの慣性モーメントを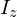 と置きます。
と置きます。
これにより、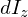 は、
は、
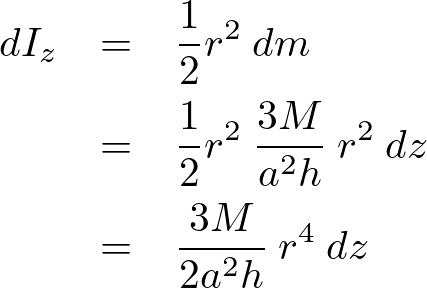
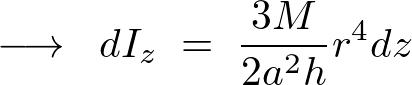
ここで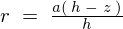 により、
により、
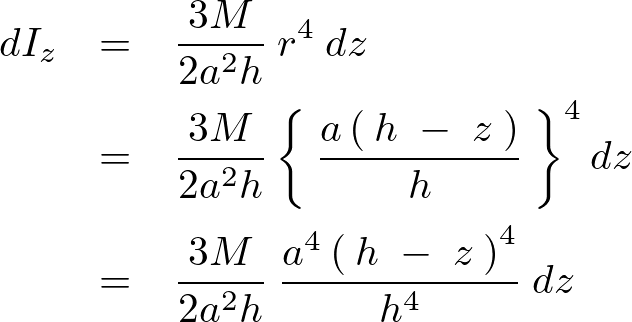
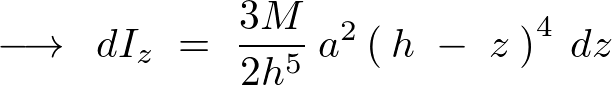
これを全体にわたって積分していきます。
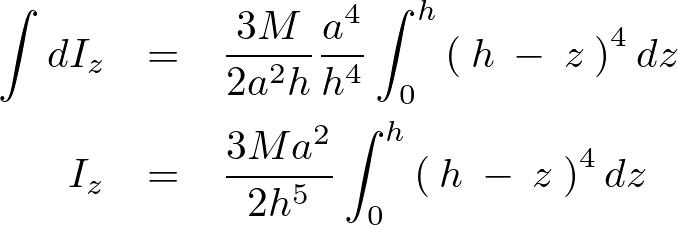
ここで上記積分を実行するために変数変換を実施します。
次のように置きます。
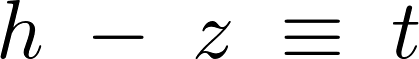
これを![]() で微分すると、
で微分すると、
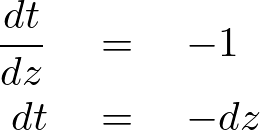
このことにより積分範囲は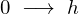 ではなく次のように変更になります。
ではなく次のように変更になります。
よって円錐の慣性モーメントの積分範囲は以下のようになります。


この積分範囲の変更によって積分計算をしていきます。

これより円錐の![]() 軸周りの慣性モーメントは以下のように求まります。
軸周りの慣性モーメントは以下のように求まります。

当サイトは運営し始めて15年以上(ブラショー、サル線、よくベク、よく慣が始まり)になりますが、私が学生時代のころ円錐に関する慣性モーメントが載っているテキストは見たことがありませんでした。
その当時からあったサイトは私の知っている限りでは物理のがきしっぽ様、そのちょっと後に高校数学の美しい物語様などがありますがそのサイトでも同様の結果になっているので円錐の![]() 軸周りに関する慣性モーメントの計算結果はこれであっているかと思います。
軸周りに関する慣性モーメントの計算結果はこれであっているかと思います。