半球体の慣性モーメントの導出過程
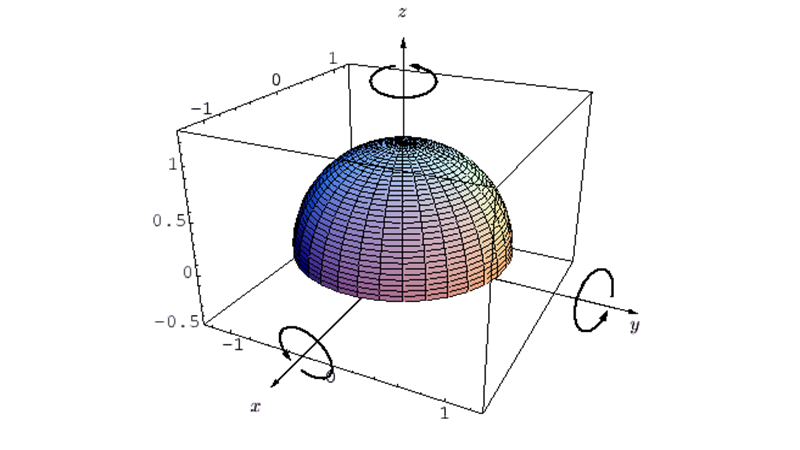
半球体の重心を通る軸に関する慣性モーメントの導出
【Ⅰ】質量が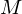
、半径が
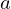の半円球の重心を通り底面に平行な軸に関する慣性モーメント
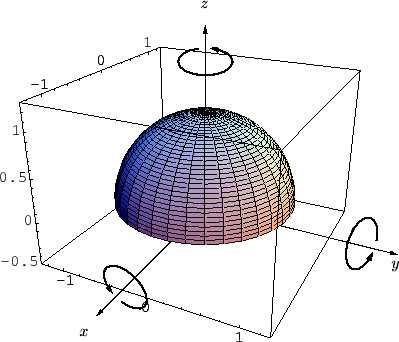
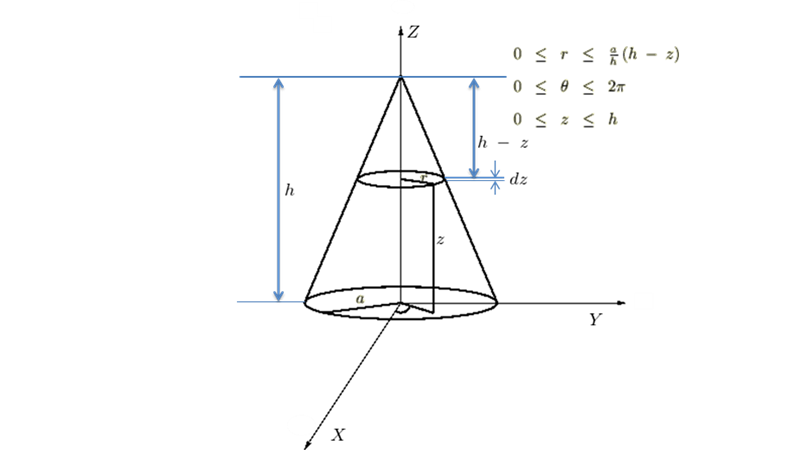
図の半球体の体積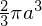は
、質量はとします。
体積密度は、
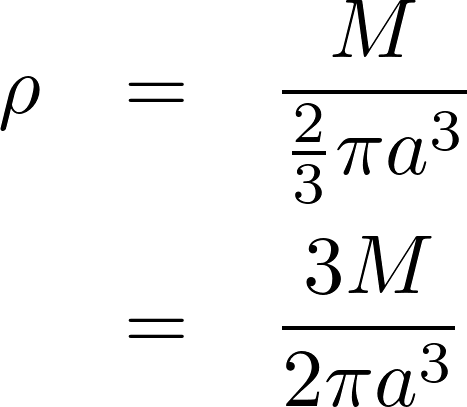
回転軸（
軸とします）からの距離は、
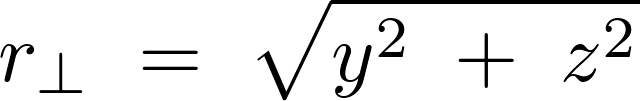
極座標を使えば、
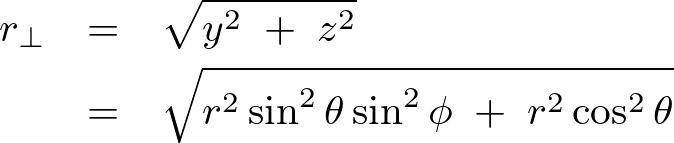
これらにより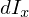
は、
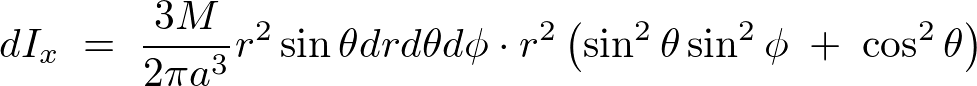
たし上げます。
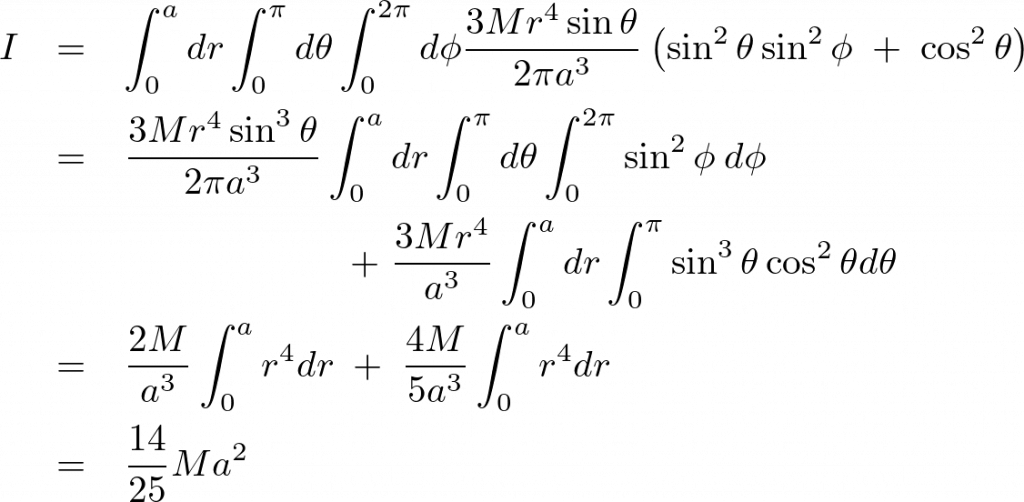
よって半球体における半径がの半円球の重心を通り底面に平行な軸周りの慣性モーメントは以下のようになります。
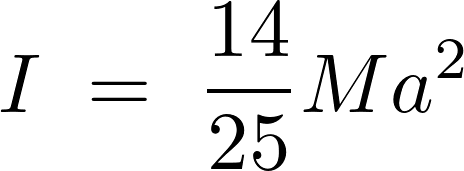
なお、上記計算途中の式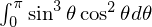
の積分はチャプター１に出てきた三角関数の積分公式を適用し次のように計算しています。
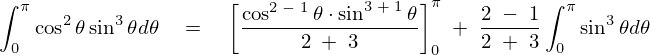
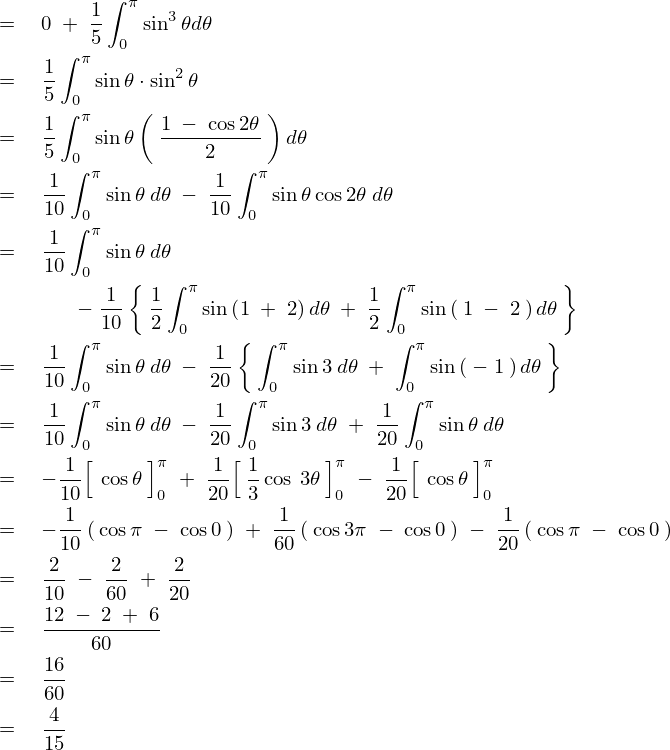
【Ⅱ】半円級の重心を通る対称軸に関する慣性モーメント
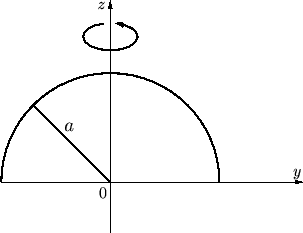
半径をとし、
軸を回転軸とします。
この時の半円球に関しての慣性モーメントを導いていきます。
回転軸からの距離は、
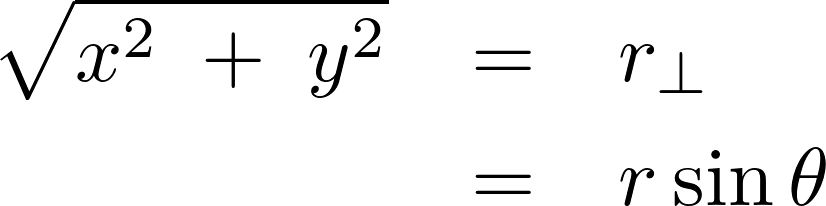
体積密度は先ほどと同じなので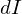
は、
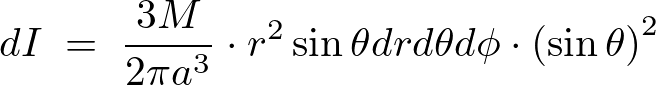
積分範囲に気を付けてこれをたし上げます。
よって以下のように求まります。
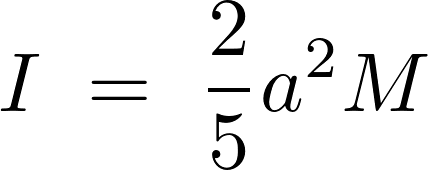
くり抜き円盤の慣性モーメント
くり抜かれた円盤の慣性モーメントに関して、平行軸の定理を利用して目的とする円盤の慣性モーメントの導出に関して詳しく解説していきます。
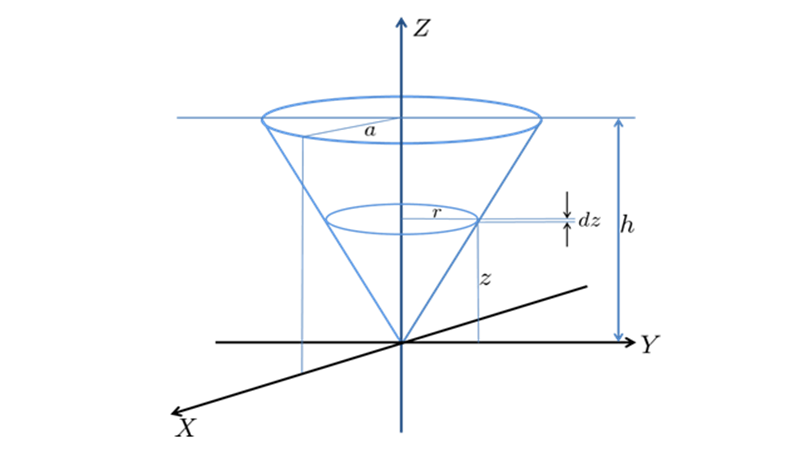
円錐の慣性モーメント-2
円錐の頂点周り、円錐底面に平行で中心点を通る軸周りの慣性モーメント、さらには円錐の重心回りの慣性モーメントについて考察していきます。
コリオリの力とは
フランスの科学者で軍属でもあったガスパール・ギュスターブ・コリオリ
初歩的な力学の分野において慣性系に関する話の中にコリオリの力というものがあります。
この“コリオリ”とは人の名前であり地球が回転することによっておこる見かけの運動力を、回転座標上で移動したときの移動方向と垂直な方向に受ける慣性力の一種を数式で表現したものになります。
一般的にこのコリオリという人物は科学者という記述が多いのですが実は軍人でもあったことはあまり知られていないようです。
北半球において大砲を撃ったとき、その弾道が標的よりもわずかに右にずれることを数式によって説明した人物ということで自衛隊でも多少知られた存在らしく、話の小ネタとして話題になることもありました（おそらく重迫撃砲(ヘヴィモータ)などではコリオリの力による弾道補正が必要になるためだと思います）。
回転座標で運動する物体
円運動の角度を
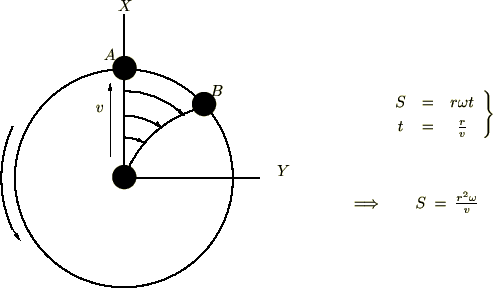
、周囲に沿った距離を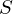
、ボールの速度を
、慣性力を
とおくと、
上の図は、矢印の通りに回転させた円盤を真上からみたものであり、中心から外側へ投げた球があたかも右のほうへずれたように見えるその様子を表したものです。中心部分にいる人物は図の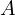
の方向へ投げたつもりが
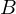のほうへまるで曲がって投げたように見えてしまいます。
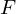はは動径方向に垂直な方向に働く慣性力とし、一定加速度での移動距離は
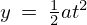の形で表せるので、
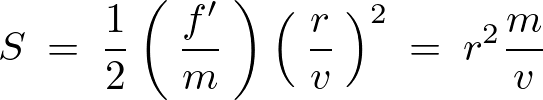
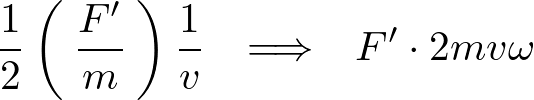
この力をコリオリの力と呼び、回転座標系で運動する物体に加わる慣性力のことを言います。
この力を実際に数式を使って具体的に表現してみましょう。
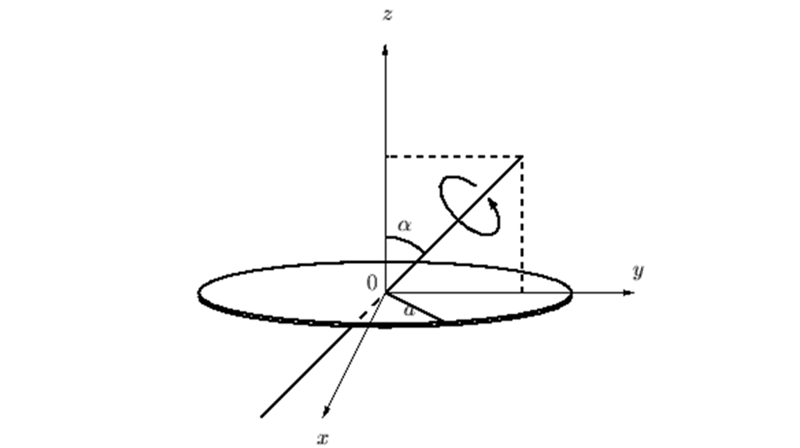
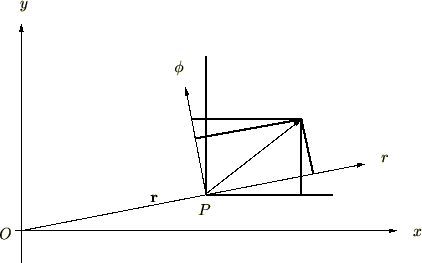
左の座標系が3次元での回転、右の座標系の図が２次元での回転を表したものになります。
これより回転座標系において時間変化した角度をとすれば以下のように表せます。
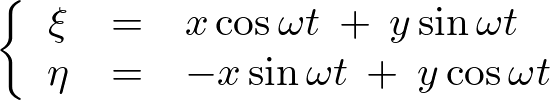
または、
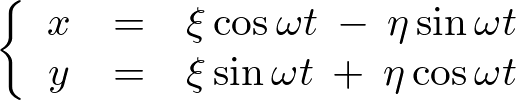
これを時間で微分します。
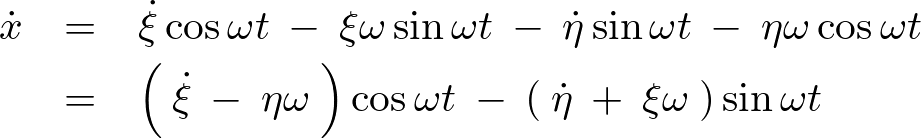
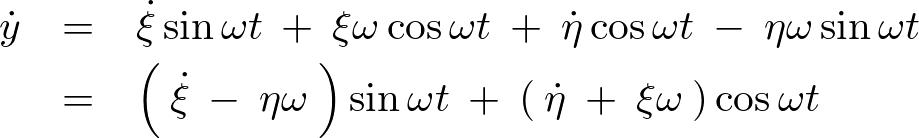
上記式を再度時間微分します。
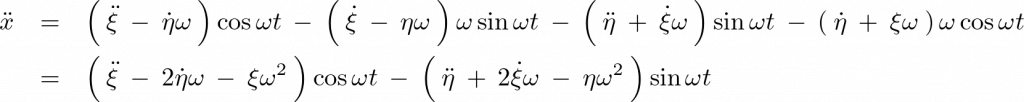
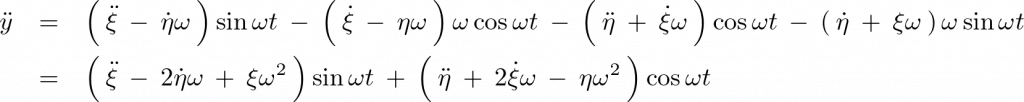
力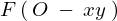
と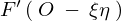
の間の関係は次式で表されます。
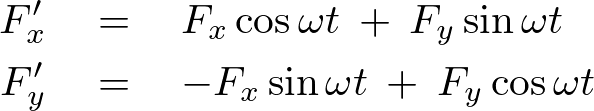
さらに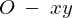
系（慣性系）では次のような運動方程式、
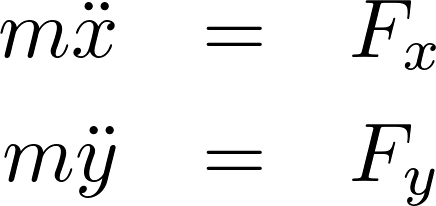
が成り立つので上の式の結果を用いて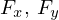
を表せば、
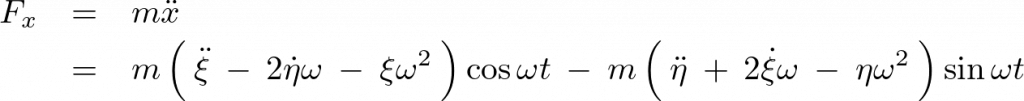
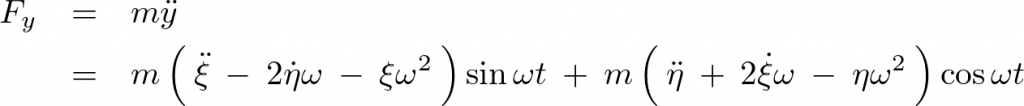
これらを代入し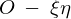
系の座標について整理すれば、
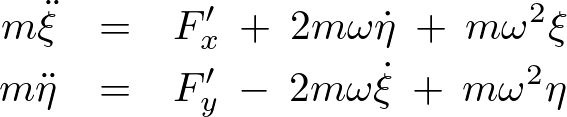
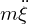は回転系座標から見た加速度運動で、運動の原因となる力として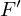のほかに2つの力が加わった形であり、右辺第2項、第3項は見かけの力（慣性力）を示しています。
右辺のそれぞれの意味は、
| 右辺第2項（コリオリの成分） |  |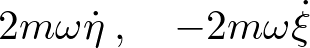
| 右辺第3項（遠心力の成分） |  |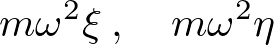
を示しています。
回転座標系をまとめてみると次のようになります。
慣性系に対して運動する座標系
ｖｖ
