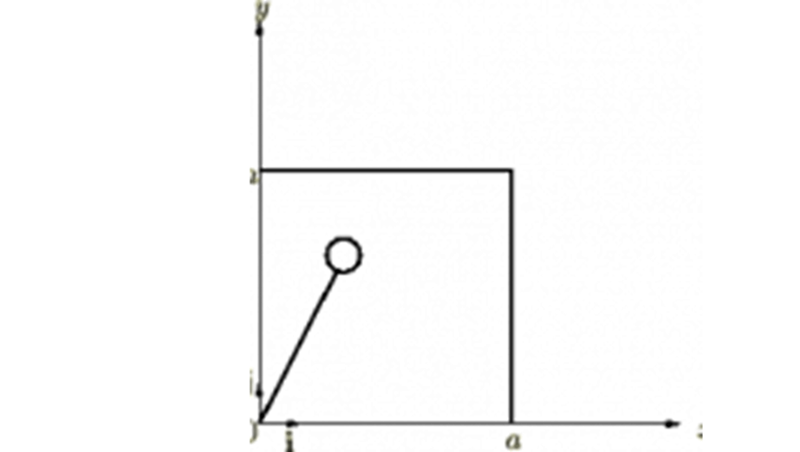質点系の力学
複数の質点からなる物理系の話
離散的な系
次に示される三質点系を考えます。
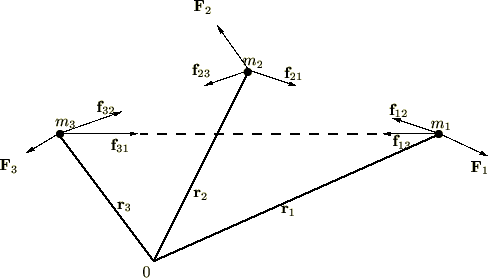
この時各質点に働く力は、
| 外力 | |
| 内力 |
さらに内外の場合、必ず作用・反作用の法則によって大きさが同じで向きが逆の一組の力があると考えます。

物理法則
上記の三質点系については次のような運動方程式が成立します。
1~3の質点の運動方程式は、それぞれ、

この をそれぞれたすと、
をそれぞれたすと、

となりますが、ここで先ほどの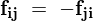 を使うと、
を使うと、 などとなるので結局、
などとなるので結局、

といった具合になります。
さらにここにおいて重心を、

とした場合、次のように表現できます。

 のところに質量
のところに質量 の質点があってそれに
の質点があってそれに (すべての外力)が働いている━
(すべての外力)が働いている━
つまりかなり大雑把な言い方になりますが は次のような区分けができることになります。
は次のような区分けができることになります。
| 離散的な系 |  |
| 連続的な系 |  |
例題① - 棒の重心
以下に示すような長さが![]() の均一な質量
の均一な質量![]() の棒の重心を求めてみましょう。
の棒の重心を求めてみましょう。

まず長さが![]() の部分の質量
の部分の質量![]() を求めます。
を求めます。
ディメンジョン1と捉えれば、この棒の線密度は、

これにより、

連続的であるので、

よって長さ![]() の棒の重心は以下のようになります。
の棒の重心は以下のようになります。

例題② - 円錐の重心

上図のような均一で質量が![]() で高さが
で高さが![]() 、底面の半径が
、底面の半径が![]() の円錐の重心を求めます。
の円錐の重心を求めます。
まず円錐の体積は、

これにより円錐の体積密度は、
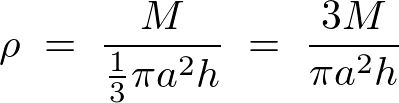
ここでは円錐の任意の高さに対する半径![]() で面積が
で面積が![]() 、厚さ
、厚さ![]() の微小厚さの円盤の質量を
の微小厚さの円盤の質量を![]() とすると、
とすると、
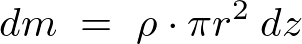
として、次のように円錐の質量を![]() と置きます。
と置きます。
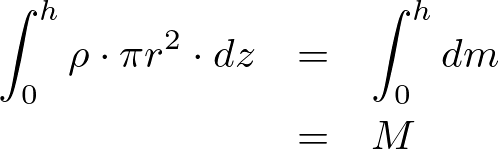
円錐の重心に関しては図から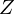 軸周りにあると考えられるので軸線
軸周りにあると考えられるので軸線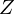 軸上の任意の点zを距離変数として採用します。
軸上の任意の点zを距離変数として採用します。
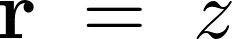
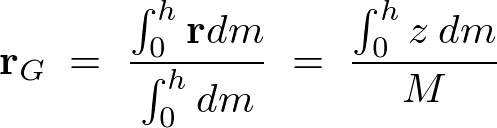
また、図中の![]() に関しては以下のような相似関係を使って導いています。
に関しては以下のような相似関係を使って導いています。
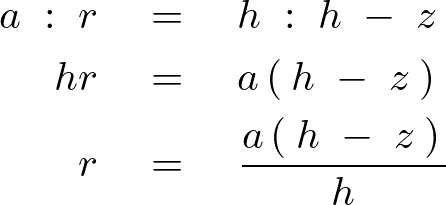
これらにより、円錐の重心は分母の円錐質量の質量Mとわかっているので上記式の分子がわかれば重心の位置が求まることになります。
上記式の分子の部分を計算していきます。
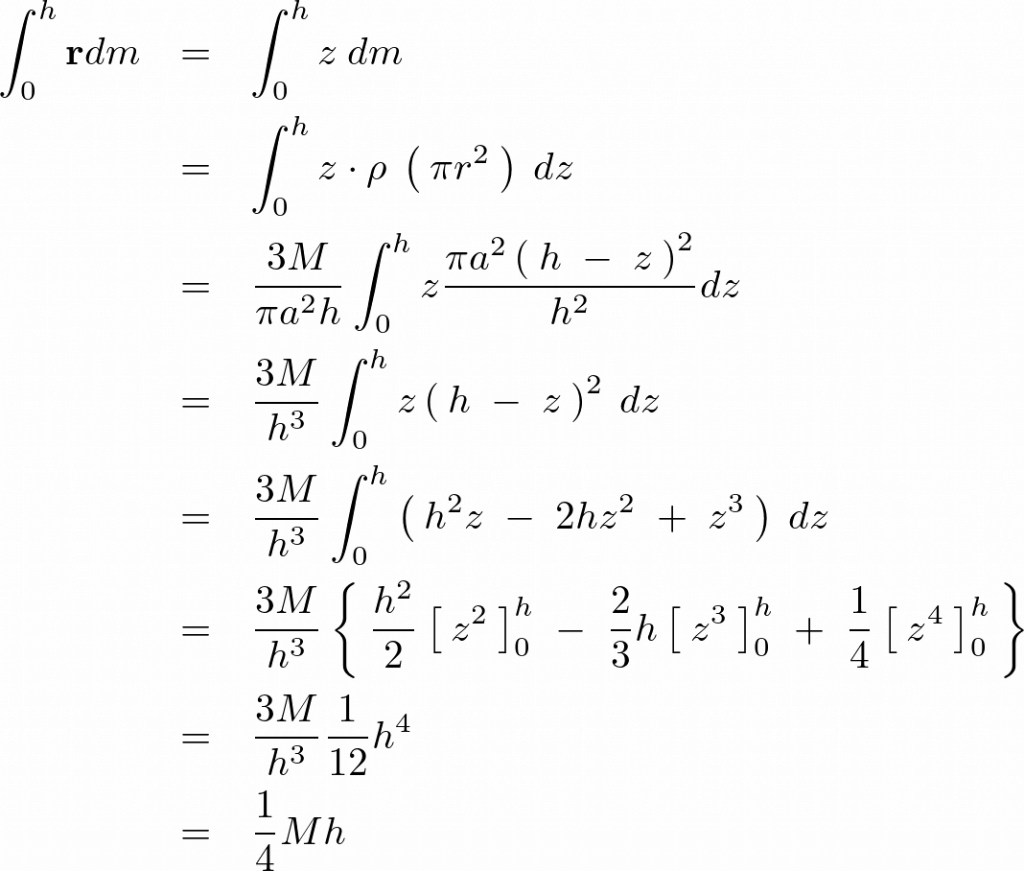
 の式に代入していきます。
の式に代入していきます。
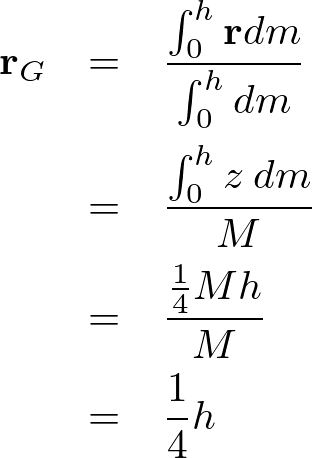
これより、円錐の重心は以下のように求まります。
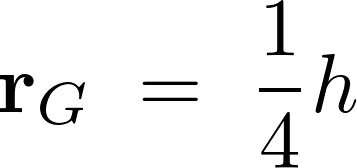
例題③ - 正方形の重心
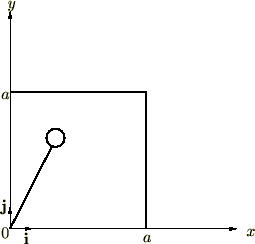
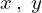 軸におけるそれぞれの単位ベクターを
軸におけるそれぞれの単位ベクターを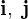 とすると、
とすると、
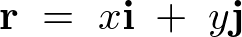
となるのでこれより、
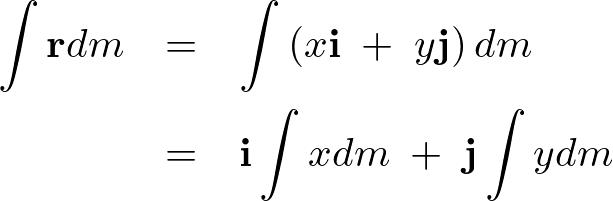
微小部分の面積は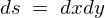 で、密度は、
で、密度は、
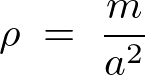
これらにより、
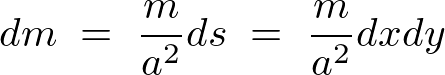
足し上げていきます。
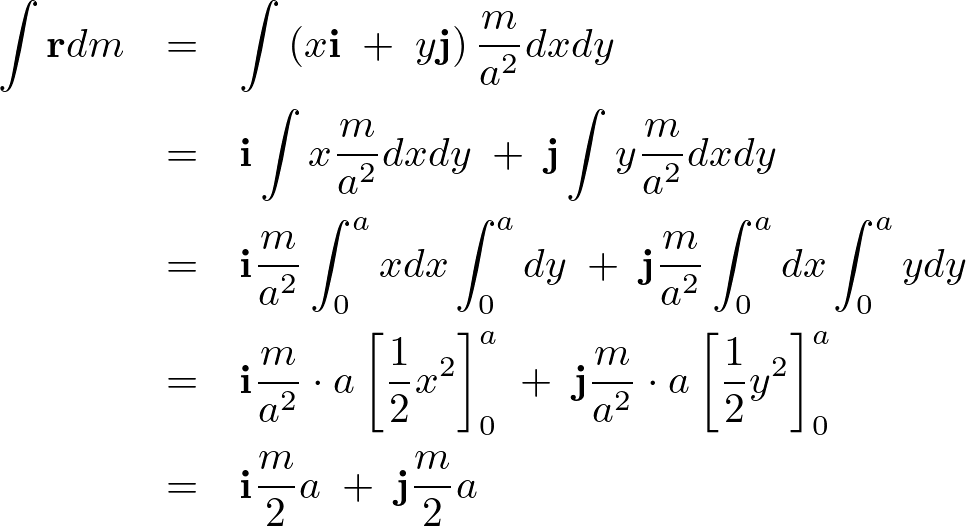
これより正方形の板の重心は、
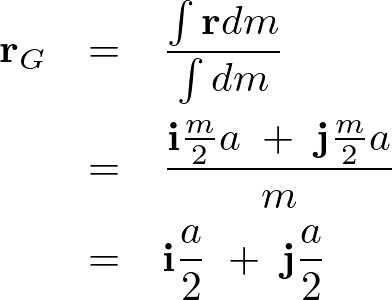
よって以下のように求まります。
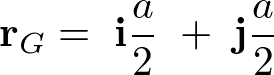

質点系の力学
複数の質点からなる物理系の内容になります。複数の質点を考えたときそれにかかわる作用反作用の力について考えていきます。

剛体の運動
剛体の運動について。剛体とは任意の2点間の距離が運動しているときに変化しないものをいいます。この時非相対論的定義を適用します。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-

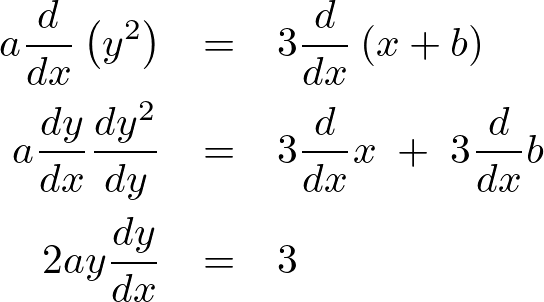

 の式を計算していきます。
の式を計算していきます。