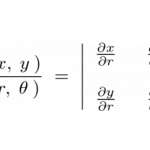微小面積要素の計算
微小面積要素の計算
関数行列式(ヤコビアン)
ある座標系 をほかの座標系
をほかの座標系 へ変えるとき、
へ変えるとき、
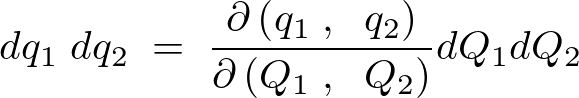
という式が成り立ちます。
この時の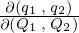 をヤコビアン(関数行列式)と呼び、次のように表せるものになります。
をヤコビアン(関数行列式)と呼び、次のように表せるものになります。
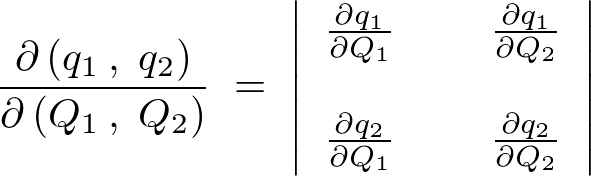
実際にデカルトから極座標への変換をこのヤコビアン(関数行列式)をつかって求めてみましょう。
まず、デカルト座標において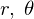 を表すと、
を表すと、
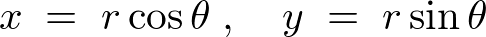
この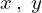 の式をそれぞれ
の式をそれぞれ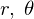 によって偏微分していきます。
によって偏微分していきます。
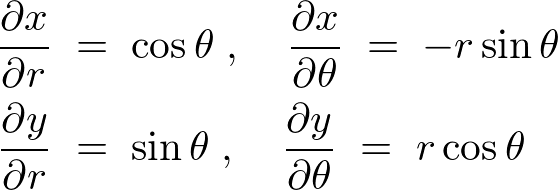
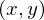 座標系から
座標系から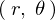 へ移行するヤコビアンは、
へ移行するヤコビアンは、
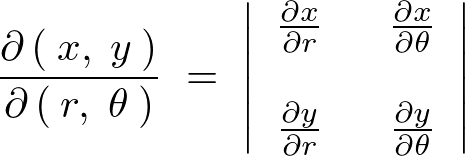
これにそれぞれを代入してこの行列式を計算していきます。
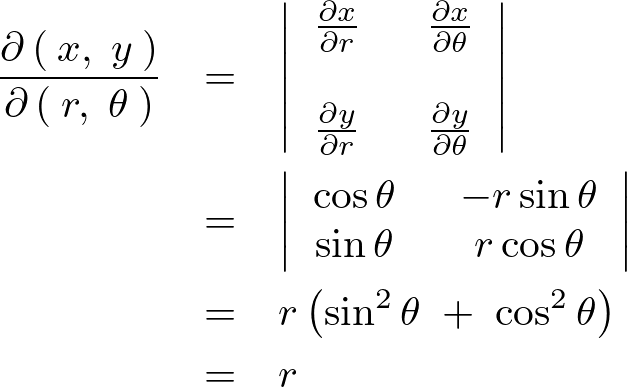
上記の計算結果を入れれば、
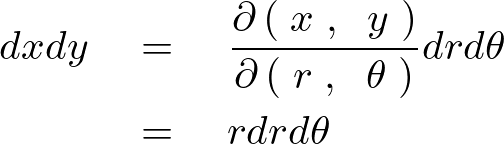
よってデカルト座標の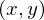 は、ヤコビアンによる平面極座標変換によって以下のように求まります。
は、ヤコビアンによる平面極座標変換によって以下のように求まります。
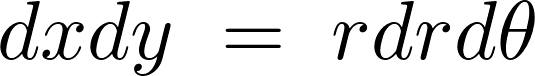
微小体積要素の移動ルート
一般的な座標![]() への移動を考えてみましょう。
への移動を考えてみましょう。
この移動のルートには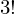 通りがあります。
通りがあります。
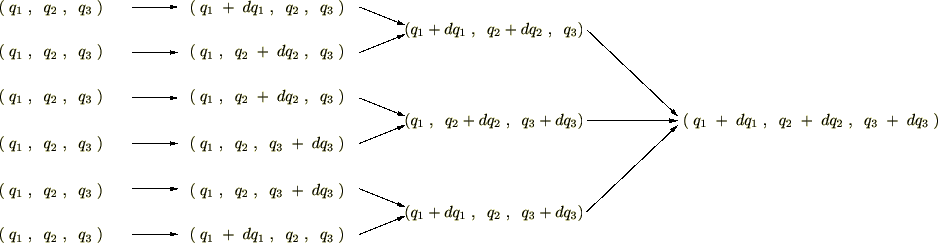
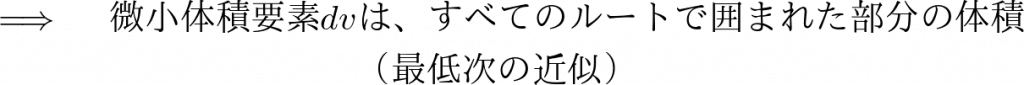
デカルト座標系
上記のルート表にデカルト座標系を当てはめていけば次のようになります。
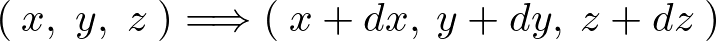
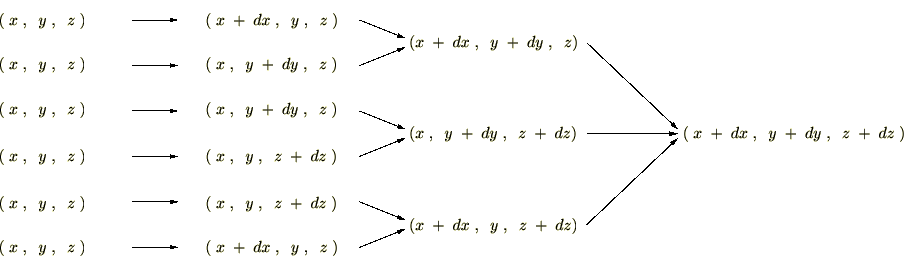
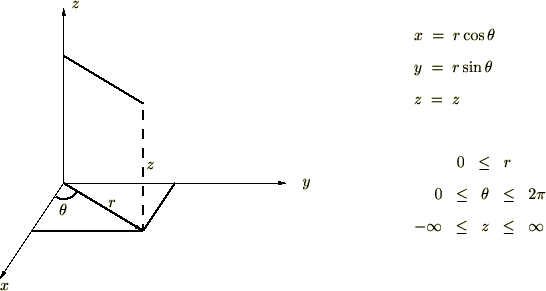
極座標系
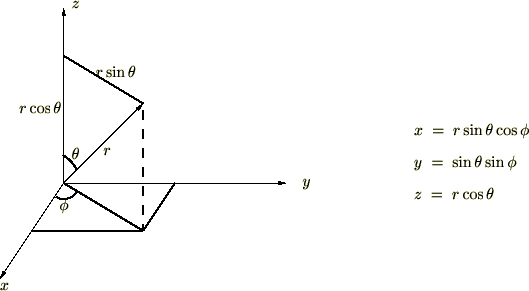
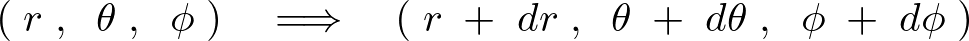
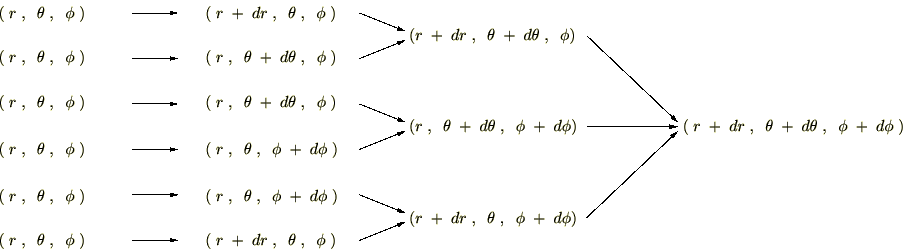
円柱座標系
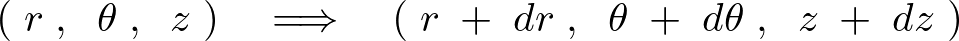
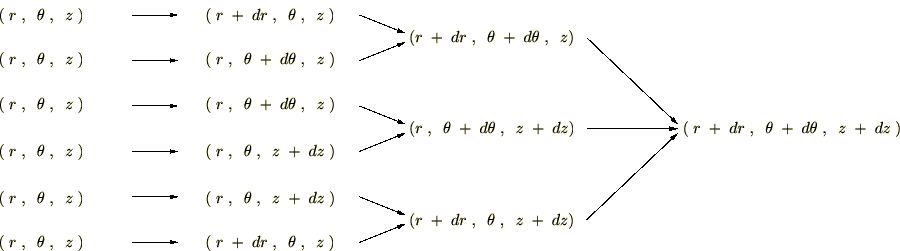
変数変換とヤコビアン
別の座標系へ対応させた場合その微小面積要素に対しどの程度のスケール変換量をスカラ倍させれば同値になるかを求めるものにヤコビアンがあります。
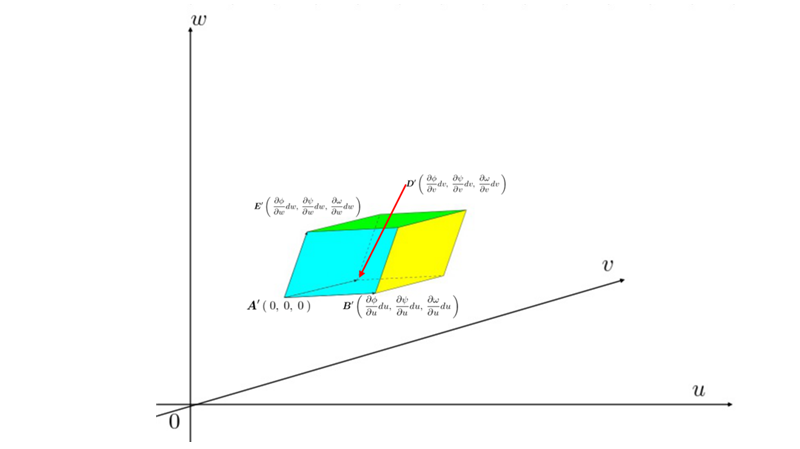
多次元量ヤコビアン
2次元スケール変換を今度は3次元に拡張した場合を考えます。それは3次元以上においてどのような意味を持つのかを考察していきます。
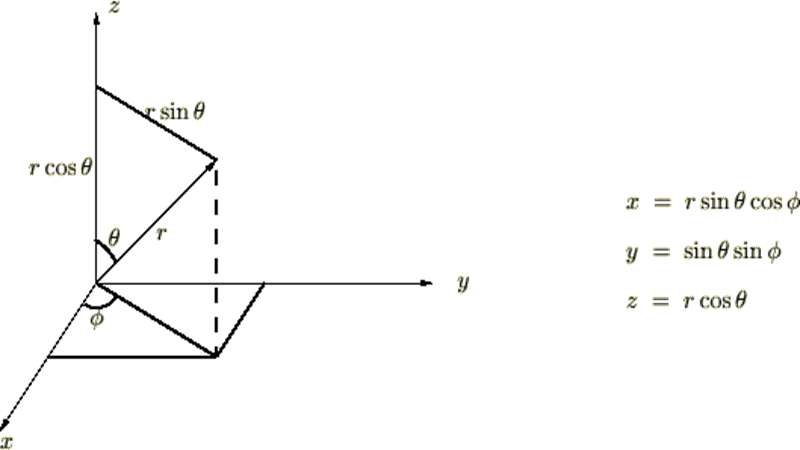
微小面積要素の計算
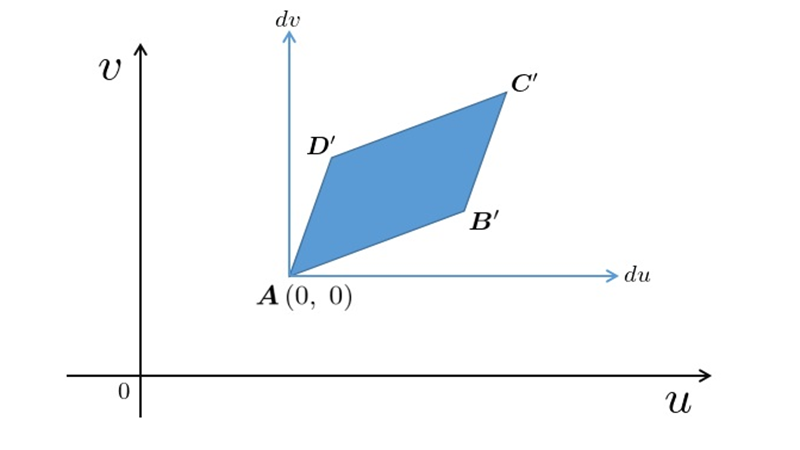
ヤコビアンを使った微小面積要素の考察をします。
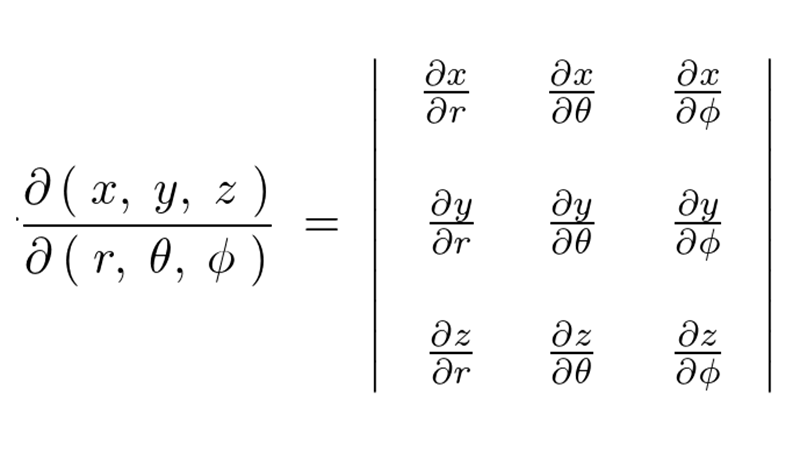
dvの計算法
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

微小体積要素の計算
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
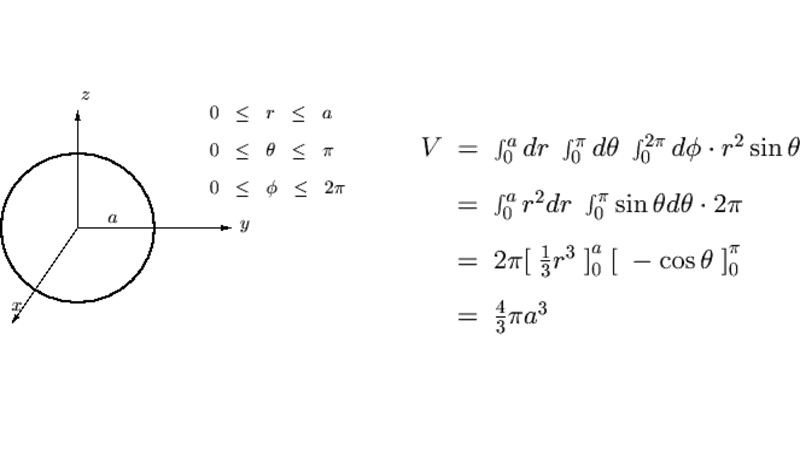
dvの計算方法-答え
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
-
-
-
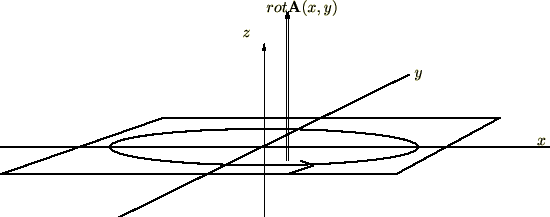
三次元ベクトル場および発散についての補足
カテゴリー : 三次元ベクトル場、発散についての補足三次元ベクトル場の発散(ダイバージェンス)に関して、ナブラとベクトル場の内積との関係について考察してみましょう…
-
-
-
-
-
-

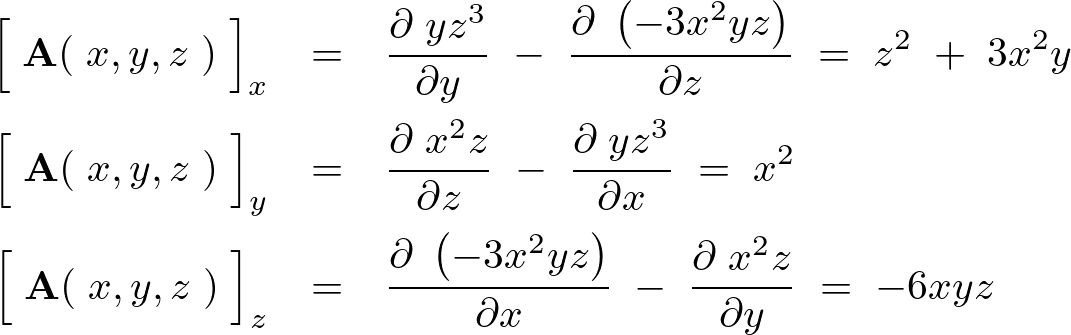
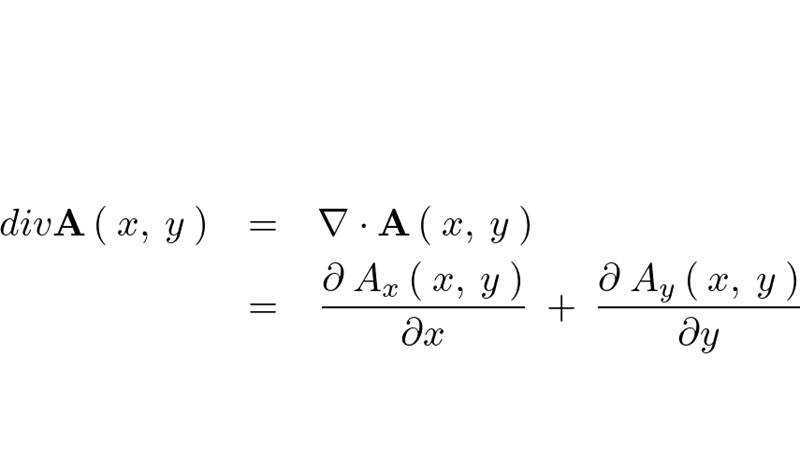
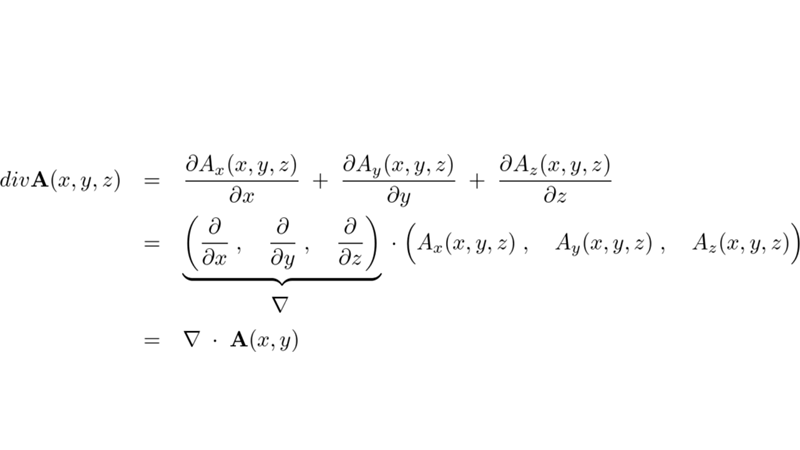
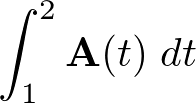
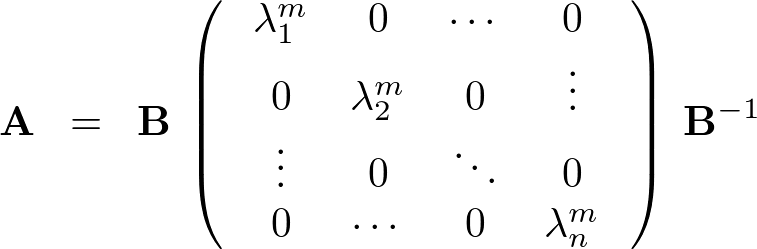
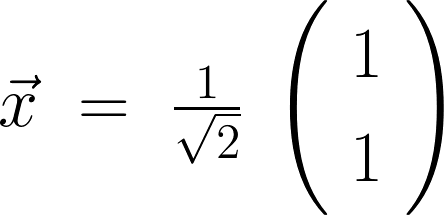
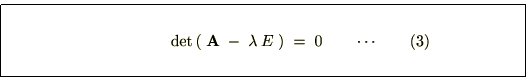
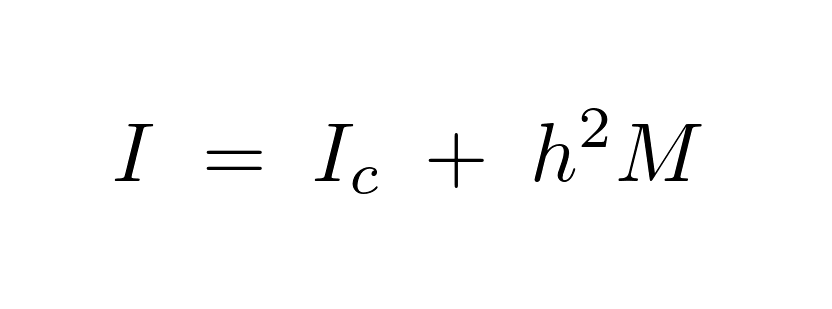

 の式を計算していきます。
の式を計算していきます。