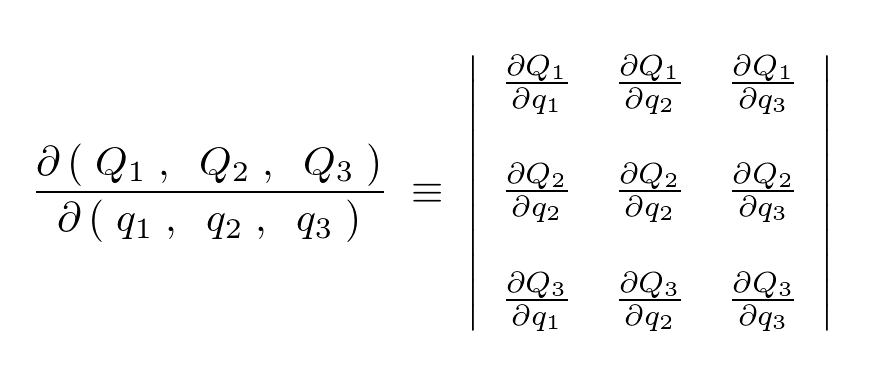dvの計算法-ヤコビアンを使うやり方
微小体積要素dvの求め方
dv計算法-ヤコビアンを使うやり方
座標系 座標系
座標系 へ座標変換するとき先ほどのセクションで出てきた関数行列式をつかうと次のようになります。
へ座標変換するとき先ほどのセクションで出てきた関数行列式をつかうと次のようになります。

ここで中央部分の行列は、

となることに注意します。分子にあたる部分が新座標系、分母にあたる部分が旧座標系というように考えます。
極座標
実際にデカルトから極へ移行するときの を関数行列式で求めてみましょう。
を関数行列式で求めてみましょう。
まず、

より、これに対する関数行列式(ヤコビアン)は次のようになります。

この関数行列式(ヤコビアン)における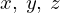 の位置表現に対してはつぎのものを使います。
の位置表現に対してはつぎのものを使います。

これらをヤコビアンの行列式の中に示されるそれぞれの偏微分の式に当てはめて計算していけば、



上記の結果によりにより極座標におけるヤコビアンは、

となるので、今度は実際にこのヤコビアンを計算していきます。
ちなみにここではサラスによる計算法ではなく、行列式展開法というやり方でその計算過程を示します。
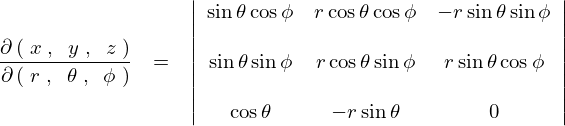
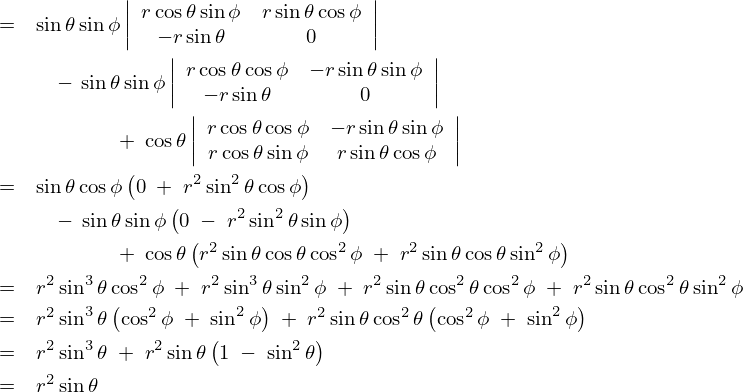
よって極座標における微小体積要素![]() は次のようになります。
は次のようになります。

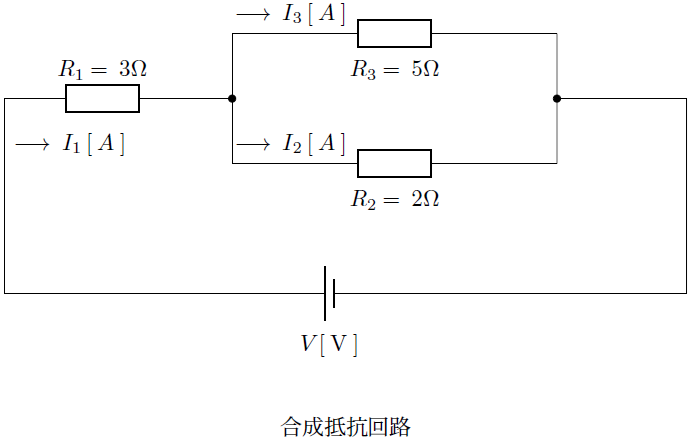
円柱座標
今度はデカルトから円柱座標へのヤコビアンを求めてみましょう。
円柱座標は、

となるので、この円柱座標に対するヤコビアンの中の偏微分の式は、
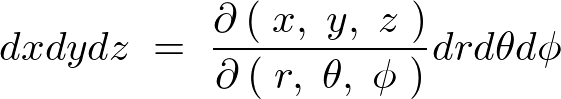

それぞれの偏微分を計算していくと、


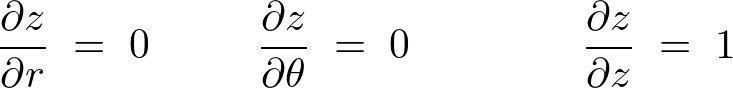
代入していきます。





よって円柱座標における微小体積要素![]() は次のようになります。
は次のようになります。

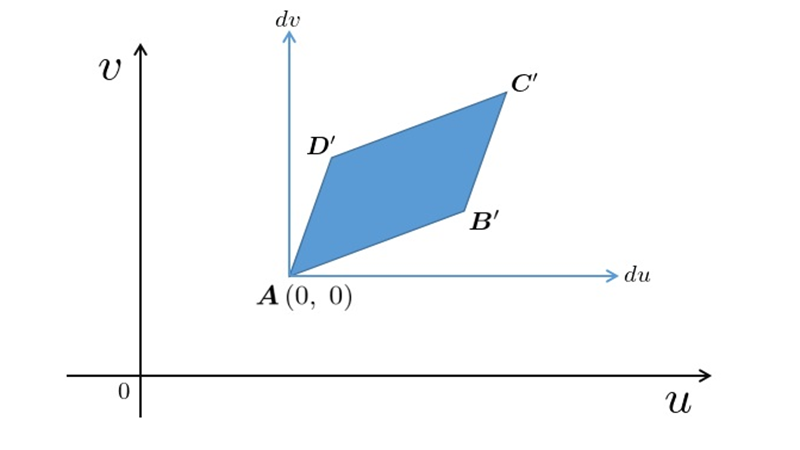
変数変換とヤコビアン
別の座標系へ対応させた場合その微小面積要素に対しどの程度のスケール変換量をスカラ倍させれば同値になるかを求めるものにヤコビアンがあります。
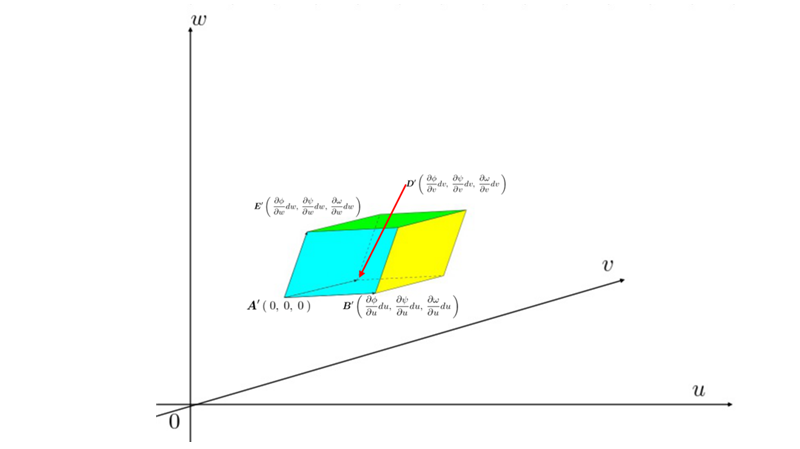
多次元量ヤコビアン
2次元スケール変換を今度は3次元に拡張した場合を考えます。それは3次元以上においてどのような意味を持つのかを考察していきます。
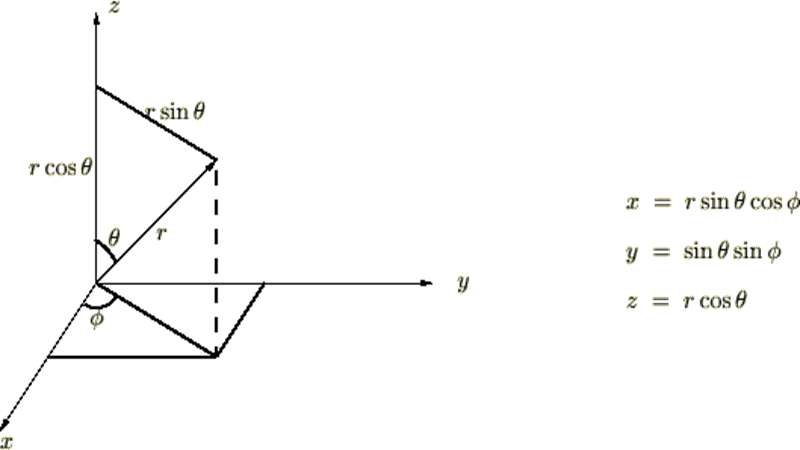
微小面積要素の計算
ヤコビアンを使った微小面積要素の考察をします。
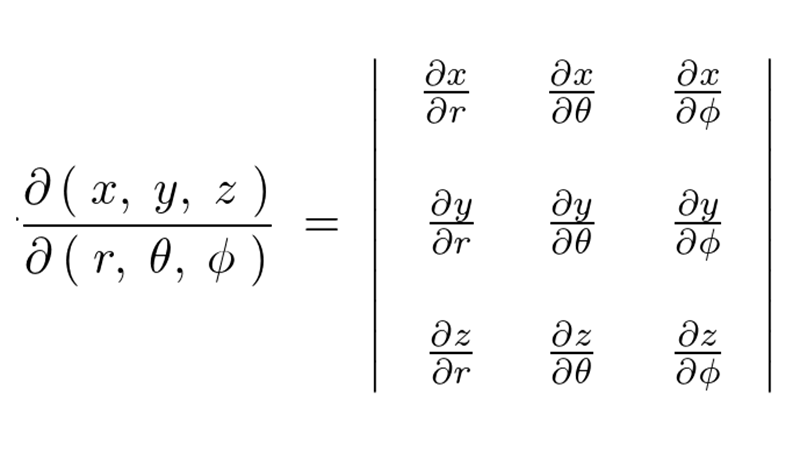
dvの計算法
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

微小体積要素の計算
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
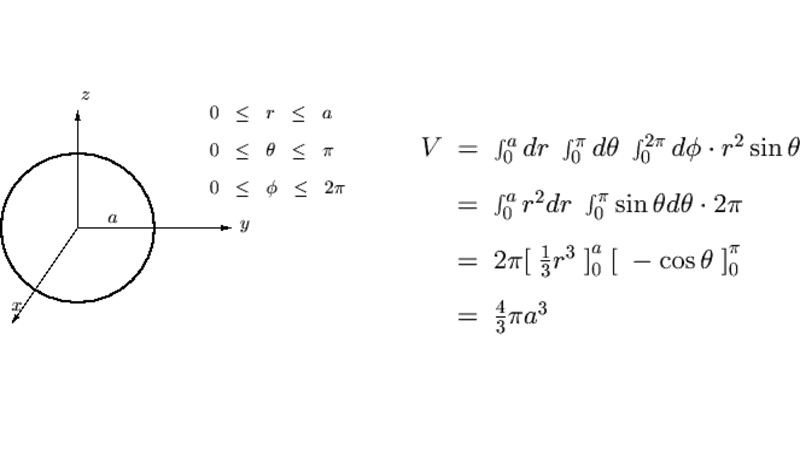
dvの計算方法-答え
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。