重積分
重積分学
2変数の積分
形としては次のようになります。
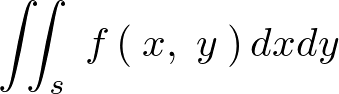
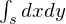 の意味
の意味

 は座標系で表現したときの微小面積になります。
は座標系で表現したときの微小面積になります。
ただしこの微小面積は座標系によって異なります。
座標系に依存しない形では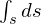 と書き、先ほどのデカルト表現においては
と書き、先ほどのデカルト表現においては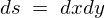 になります。
になります。
ここでこの![]() を図で考えてみましょう。
を図で考えてみましょう。
座標系が![]() のとき、
のとき、
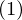 点
点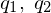 を考える
を考える
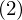 すべての変数を
すべての変数を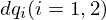 ずらす
ずらす
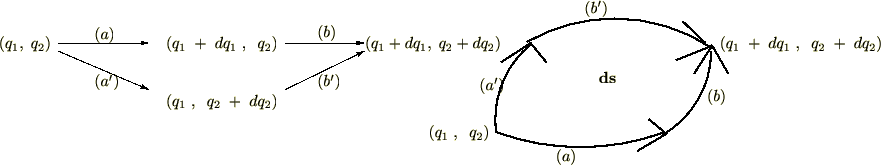
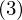 すべての経路によって囲まれた部分の面積が面積要素
すべての経路によって囲まれた部分の面積が面積要素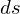 になる
になる
デカルト座標系での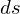
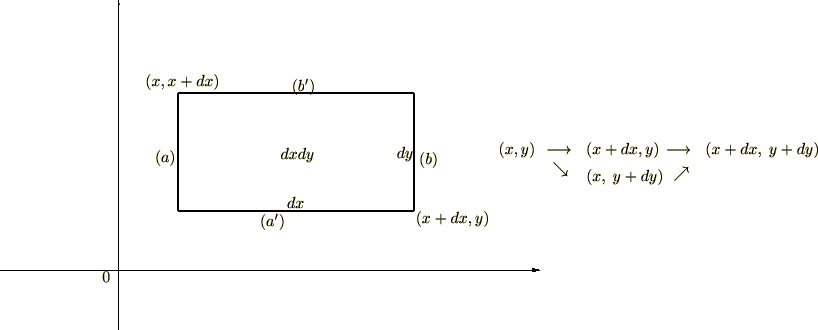
面積要素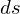 になる
になる
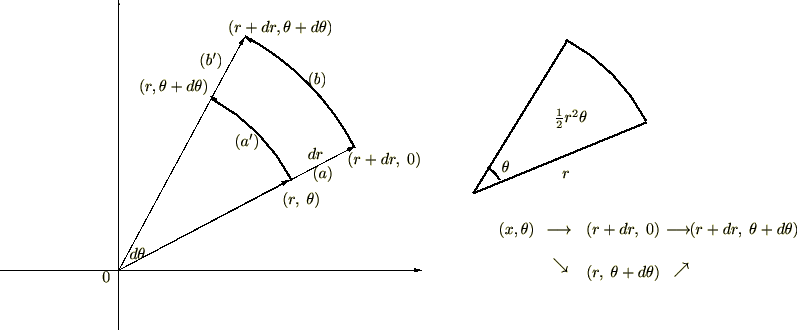
極座標における微小面積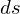 の面積の求め方
の面積の求め方
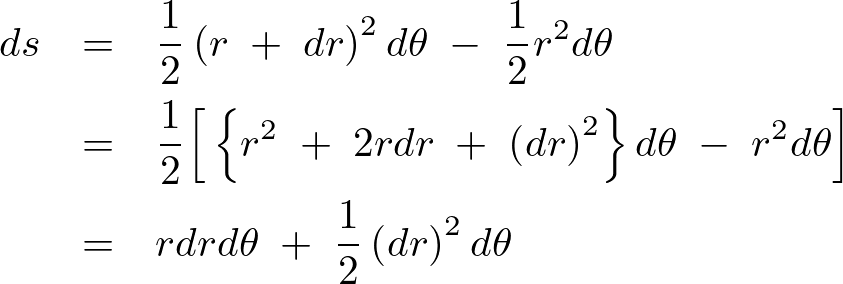
これより以下のようになります。
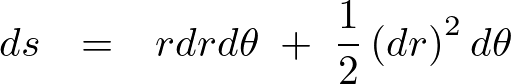
求められた上記の式において、第一項が微少量の2次、第二項が微少量の3次になります。
ひとまず、この場面においては上記の微少量の3次はキャンセルできるとしましょう。
そうすると極座標における微小面積![]() は次のように表現できることになります。
は次のように表現できることになります。
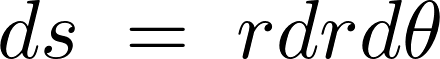
導関数
導関数について、慣性モーメントを導くのに必要な知識に関して導関数の基礎的な部分から席の微分、商の微分などについて学んでいきます。

偏微分
慣性モーメントの計算に直接かかわりませんが、変数が複数ある場合の微分について微分積分学の中の一般的な知識として取り上げておきました。

一変数関数の積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
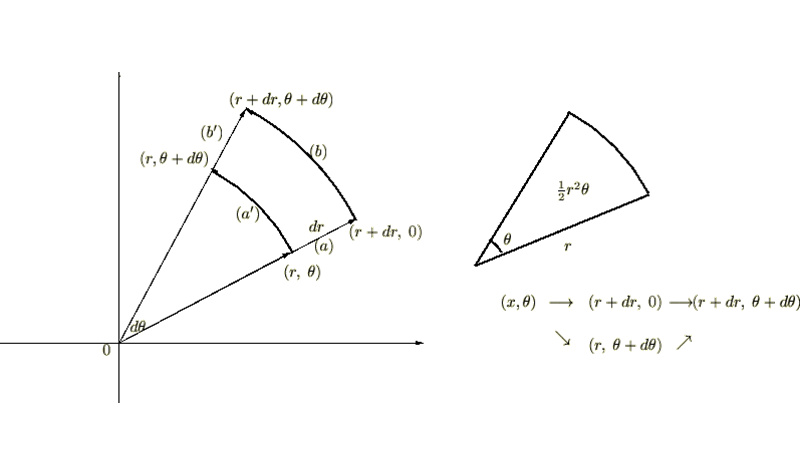
重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分例題
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-

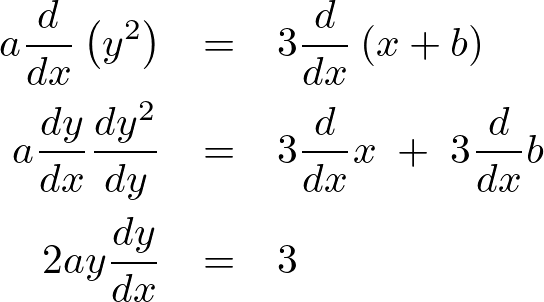

 の式を計算していきます。
の式を計算していきます。
