2重積分
2重積分の方法
重積分-考え方とその手順
積分の式 においての微小面積要素
においての微小面積要素![]() は全セクションにおいて示された極座標とデカルトの2種類が挙げられ、どちらを使って求めるかは求める面積の形によってうまく使い分ける必要があります。
は全セクションにおいて示された極座標とデカルトの2種類が挙げられ、どちらを使って求めるかは求める面積の形によってうまく使い分ける必要があります。
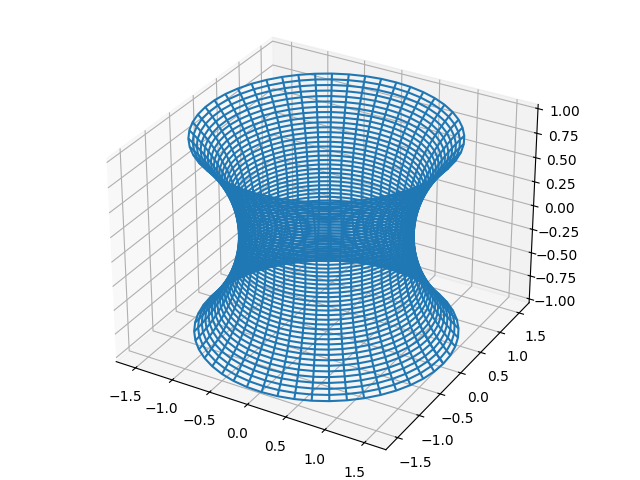
こうしたことを前提に、次に示される図形の面積を二重積分の式を使って求めてみましょう。
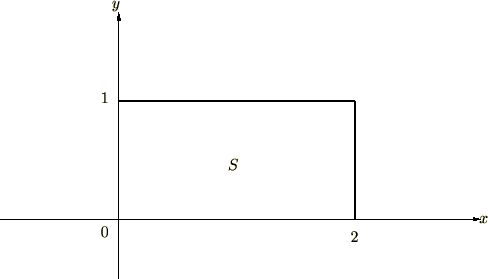
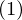 まず求める積分領域
まず求める積分領域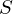 を
を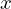 と
と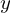 の不等式で書き表します。
の不等式で書き表します。
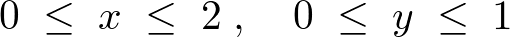
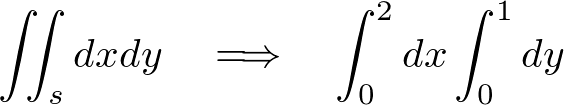
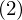 積分の実行…一つの文字ずつ積分を実行します。
積分の実行…一つの文字ずつ積分を実行します。
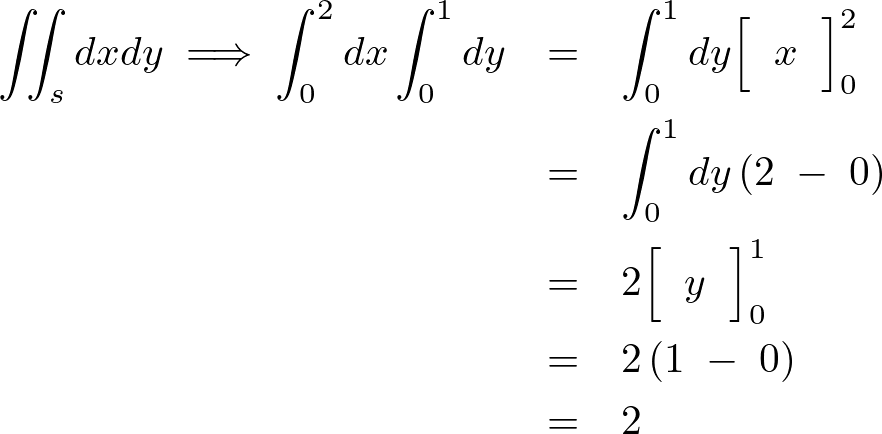
例題
今度は次の図形に対して2重積分を実行してみましょう。
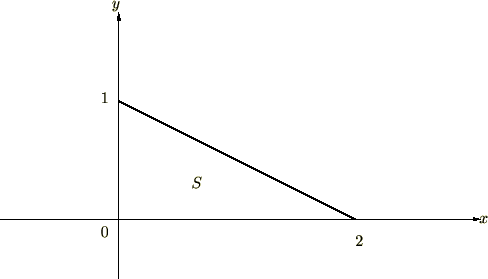
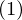 最初に積分領域を求めますが、ここで先ほどのやり方を模倣すれば、
最初に積分領域を求めますが、ここで先ほどのやり方を模倣すれば、
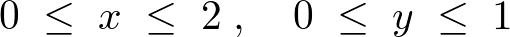
としたくなりますがこれは間違いで、こういった図形の場合、まず2つの変数のうちの1つだけを勝手に動かすという作業をします。
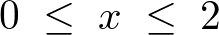
このようにしたら次にもう一つの変数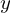 の制限を考えます。
の制限を考えます。
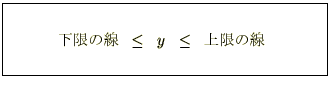
下限における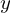 の値は
の値は 。
。
上限における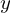 の値は
の値は 。
。
これにより、
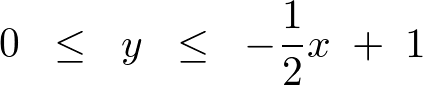
となります。したがって、
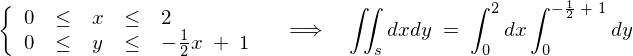
といった形になります。
こういった図形に対しての重積分は多少注意が必要です。
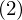 積分の実行
積分の実行
※このときにおける積分順序は積分領域の中に他の変数を含んでいるものから先に実行するようにしてください。
なのでこの積分計算においてはまず![]() からになります。
からになります。
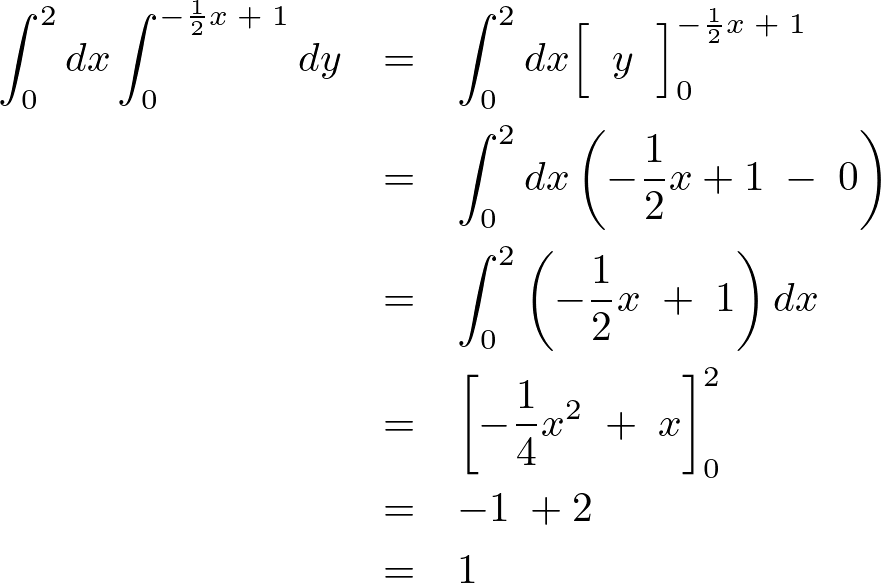
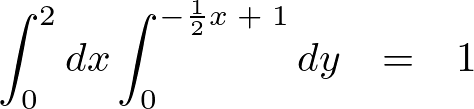
同じ問題において、今度は最初に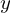 を動かした場合をやってみると積分領域は、
を動かした場合をやってみると積分領域は、

実際に計算してみると、
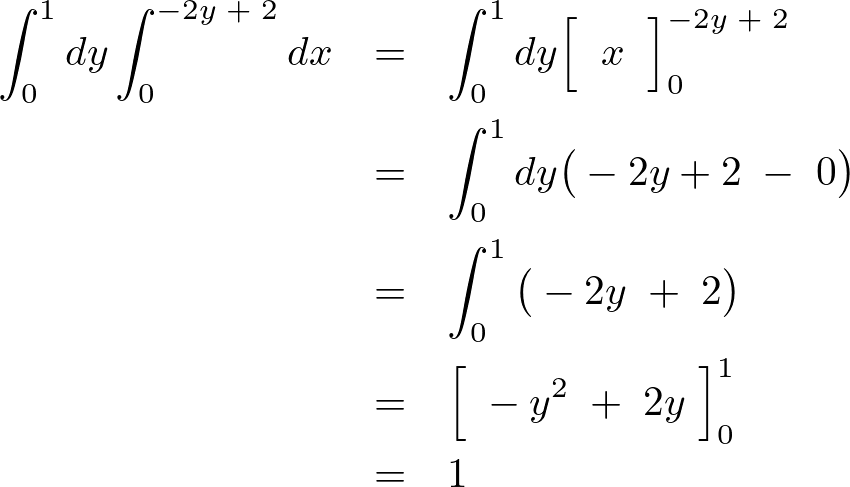
導関数
導関数について、慣性モーメントを導くのに必要な知識に関して導関数の基礎的な部分から席の微分、商の微分などについて学んでいきます。

偏微分
慣性モーメントの計算に直接かかわりませんが、変数が複数ある場合の微分について微分積分学の中の一般的な知識として取り上げておきました。

一変数関数の積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
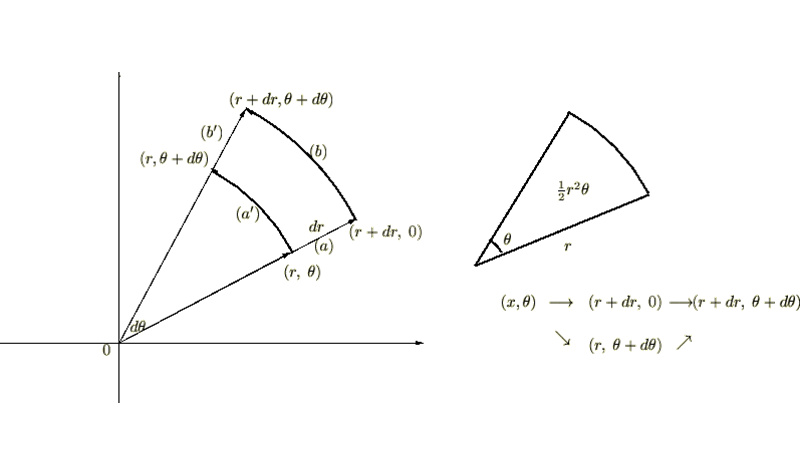
重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分例題
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-

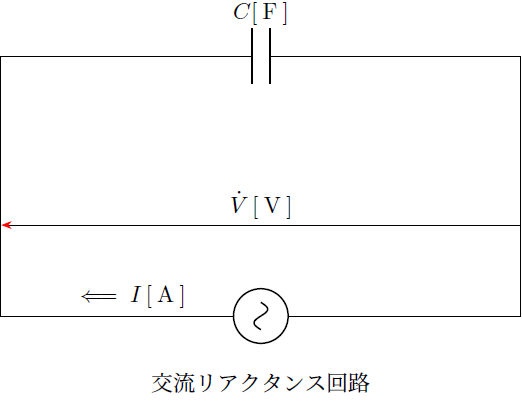
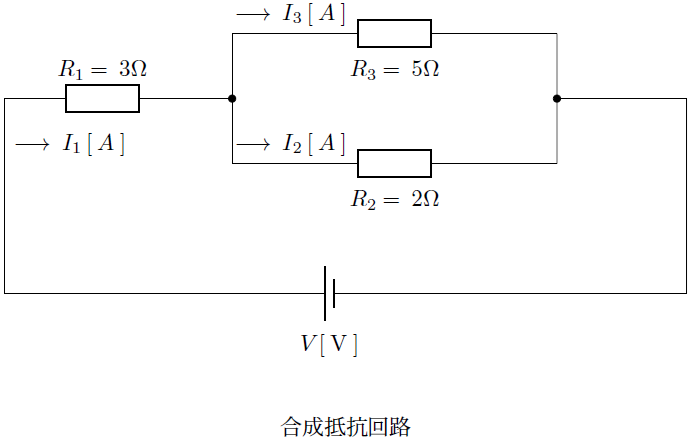
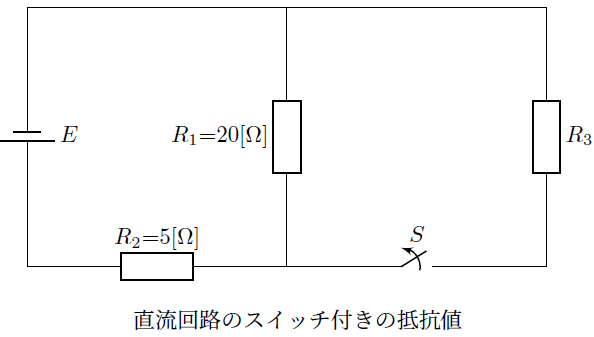

 の式を計算していきます。
の式を計算していきます。
