2重積分の例題
2重積分例題
例題①
以下の図に示される2つの直線に囲まれた面積 に対して重積分を使って求めてみましょう。
に対して重積分を使って求めてみましょう。

やり方としては、まず求める面積を![]() とし、それを右図のように2つに分割してそれぞれを
とし、それを右図のように2つに分割してそれぞれを と置きます。
と置きます。
 の間では、
の間では、

さらに、 の間では、
の間では、

といった感じで積分領域を区分けし、これを計算していきます。

例題②
底辺の長さが![]() 、高さが
、高さが![]() の二等辺三角形の面積。
の二等辺三角形の面積。
3つの頂点の座標を とします。
とします。
領域を図のように の二つに分けて考えます。
の二つに分けて考えます。
 の計算
の計算

から、直線の方程式より、

これが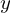 方向の上限になります。
方向の上限になります。
以下のように積分領域を決定して計算していきます。


 の計算
の計算

より、先ほどと同様にして直線の方程式に代入して計算していきます。

これが における
における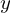 方向の上限になります。
方向の上限になります。
同様にして積分範囲を決定して計算していきます。


足し合わせます。

これより以下のように求まります。

例題③

角度 の範囲の半径が
の範囲の半径が![]() の円の面積。
の円の面積。
これの積分領域は、

よって積分の式は次のようになります。
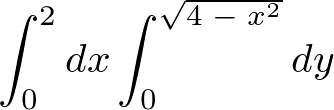
これを計算していきます。

ここで![]() という変数変換(置換積分)をすると、
という変数変換(置換積分)をすると、

となるので、


より、

例題④
半径が![]() の円の面積。
の円の面積。


ここで先ほどと同じように![]() とする変数変換をすると、
とする変数変換をすると、
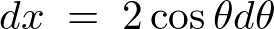
となるのでこれを代入して計算していけば、

より、

極座標の場合
ここで例題③と例題④の積分計算を今度は極座標でやってみましょう。
このデカルトから極座標へ移行する場合、

となることに注意します。
例題③極座標の場合
極座標のときの積分領域は、

これにより、

例題④極座標のとき
このときの積分領域は、

これにより、

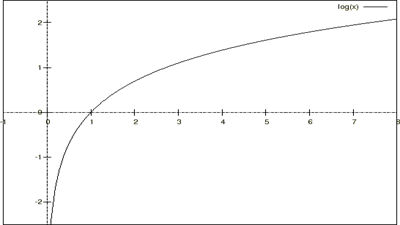
導関数
導関数について、慣性モーメントを導くのに必要な知識に関して導関数の基礎的な部分から席の微分、商の微分などについて学んでいきます。

偏微分
慣性モーメントの計算に直接かかわりませんが、変数が複数ある場合の微分について微分積分学の中の一般的な知識として取り上げておきました。

一変数関数の積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
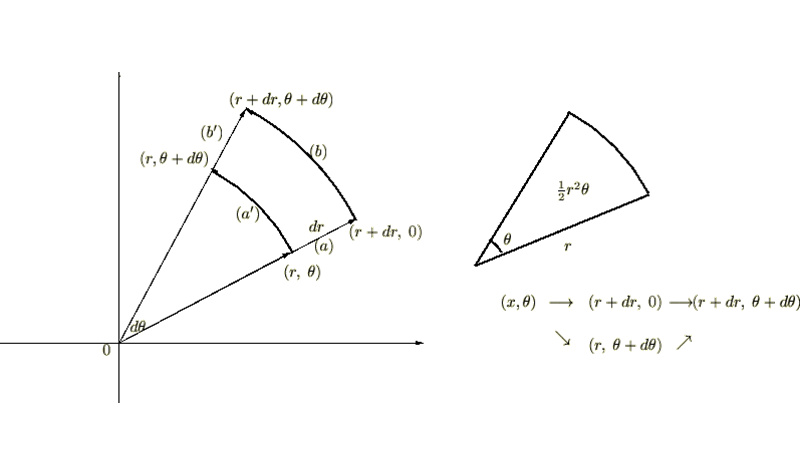
重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分例題
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-

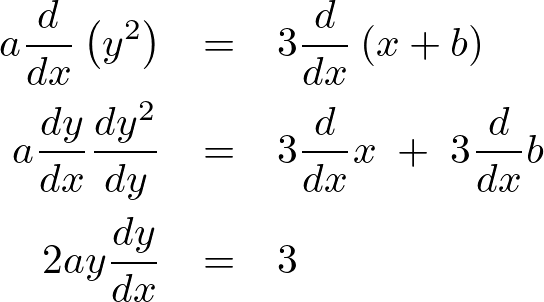
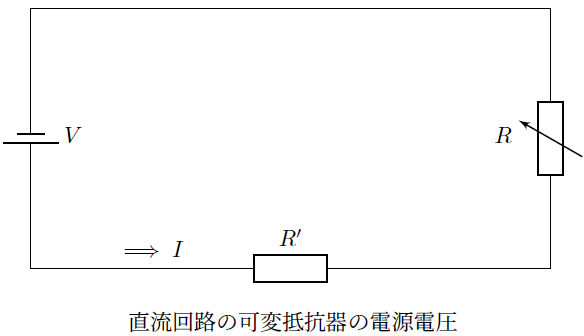

 の式を計算していきます。
の式を計算していきます。
