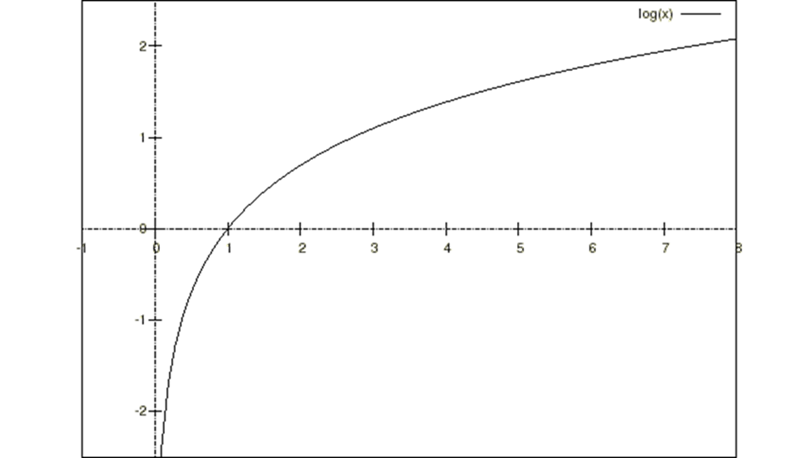導関数
導関数
導関数の定義とは
導関数の定義とは一般的に以下のように表せられます。
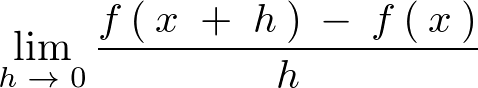
これを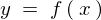 の導関数という呼び方をします。
の導関数という呼び方をします。
表記の仕方は、
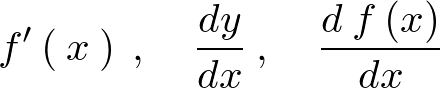
などと書きます。
上記の![]() は英語の
は英語の![]() からきており
からきており![]() は
は![]() を限りなく0に近づけるという意味を表しており最終的にはその0を代入するということを意味しています。
を限りなく0に近づけるという意味を表しており最終的にはその0を代入するということを意味しています。
まずは基本的な計算から行いましょう。
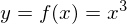 だったとします。このとき上記の、
だったとします。このとき上記の、
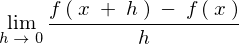
を使って計算すると、
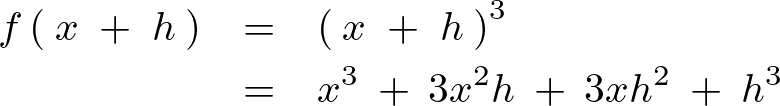
なので、これを代入すれば、
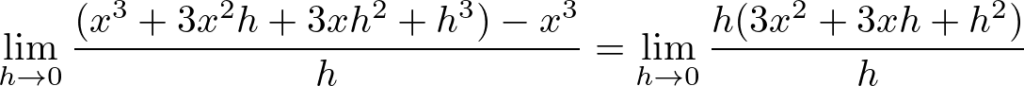
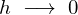 なので、
なので、
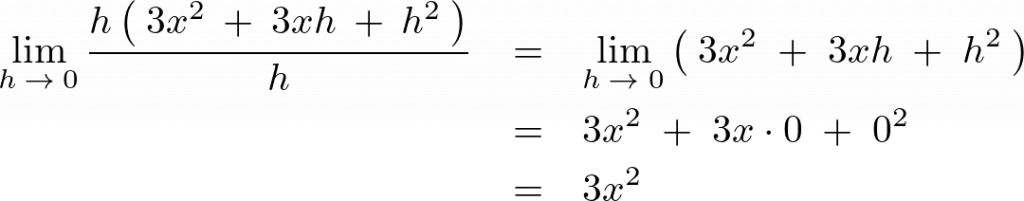
次のように求まります。
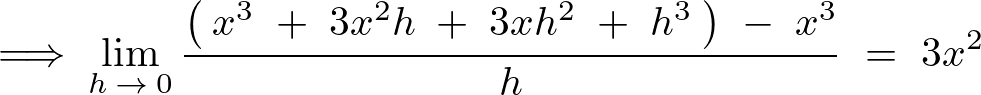
主要な微分公式
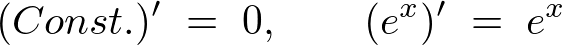
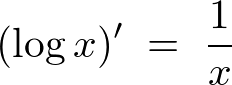
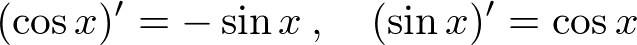
![]() というのは定数です。微分したら結果は0になります。
というのは定数です。微分したら結果は0になります。
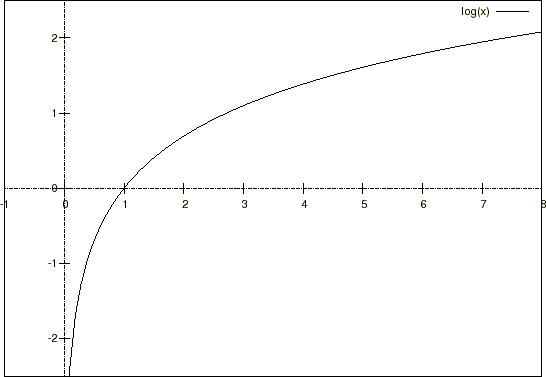
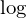 というのは対数関数です。
というのは対数関数です。![]() で微分すると
で微分すると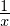 という結果になります。
という結果になります。
![]() は指数関数であり、呼び方はただのイーか、でなければイクスポーネンシャルなどと言ったりします。これは微分しても積分しても同じ結果が出てきます。ただし乗数部分にいろんな変数が乗っかっている場合は注意が必要です。
は指数関数であり、呼び方はただのイーか、でなければイクスポーネンシャルなどと言ったりします。これは微分しても積分しても同じ結果が出てきます。ただし乗数部分にいろんな変数が乗っかっている場合は注意が必要です。
なお、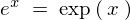 という表記もあり、これは乗数部分を見やすくする場合に使ったりします。
という表記もあり、これは乗数部分を見やすくする場合に使ったりします。
具体的な中身を書くと以下のようになります。
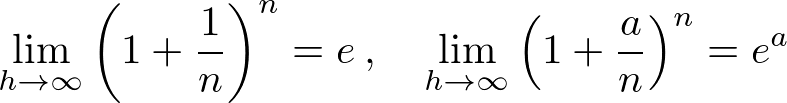
グラフは以下のようになります。
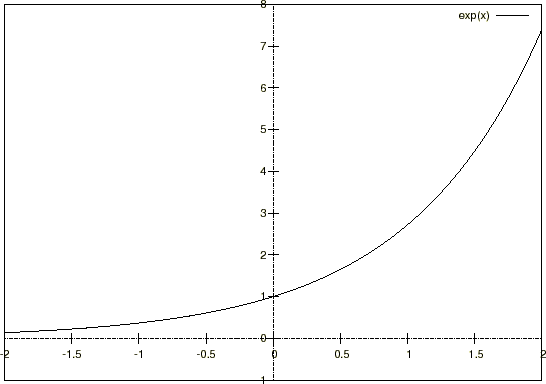
グラフからわかるように、
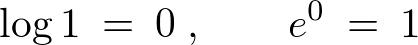
積の微分
2つの関数が積の形になっているときの微分は次のようになります。
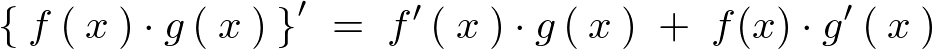
この公式を利用し、次に示す商の微分をやってみましょう。
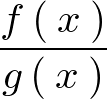
この式は、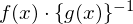 と表せるかと思います。
と表せるかと思います。
上記の公式を使うと、
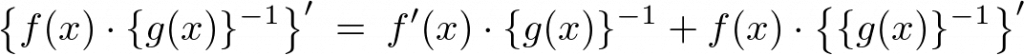
となります。
一般的には、
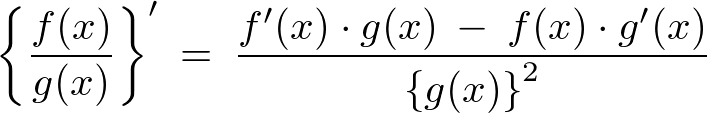
などと書きます。
問題
次に示す関数をxについて微分してみましょう。

答え
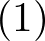
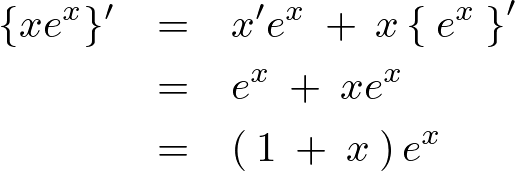
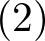
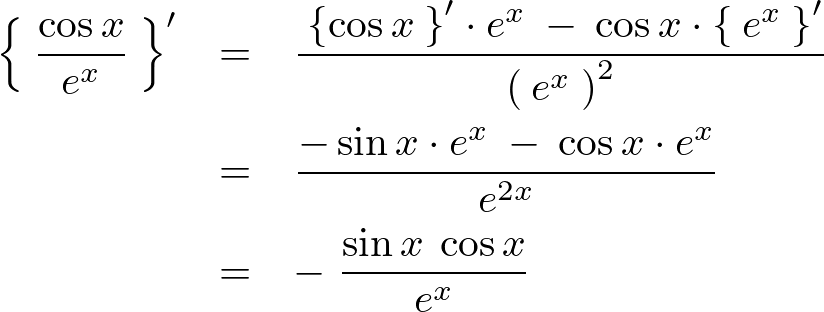
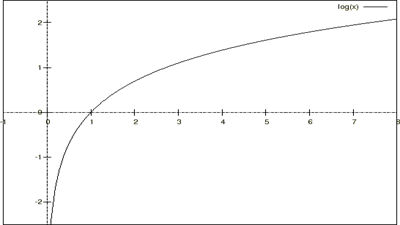
導関数
導関数について、慣性モーメントを導くのに必要な知識に関して導関数の基礎的な部分から席の微分、商の微分などについて学んでいきます。

偏微分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

一変数関数の積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
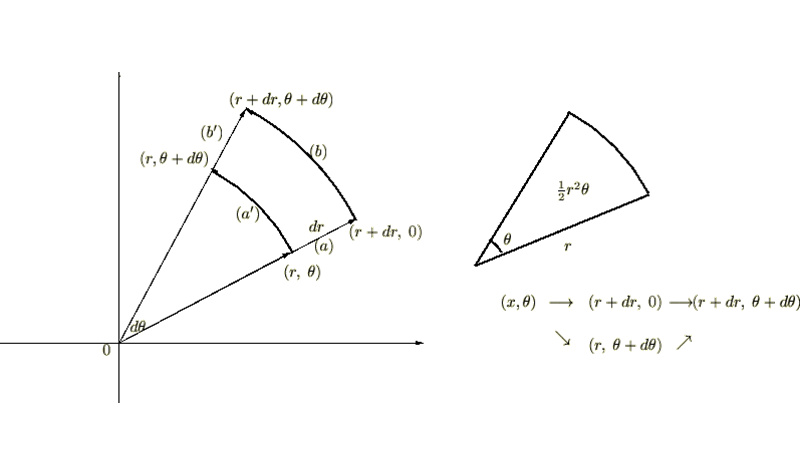
重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

2重積分例題
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.


 の式を計算していきます。
の式を計算していきます。