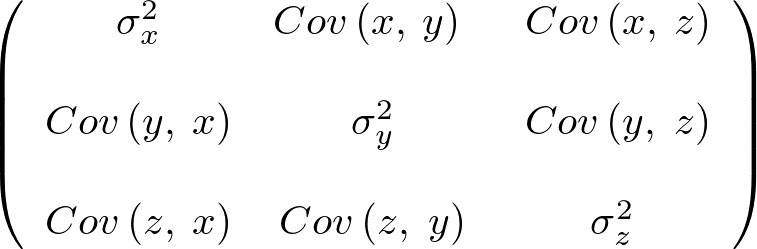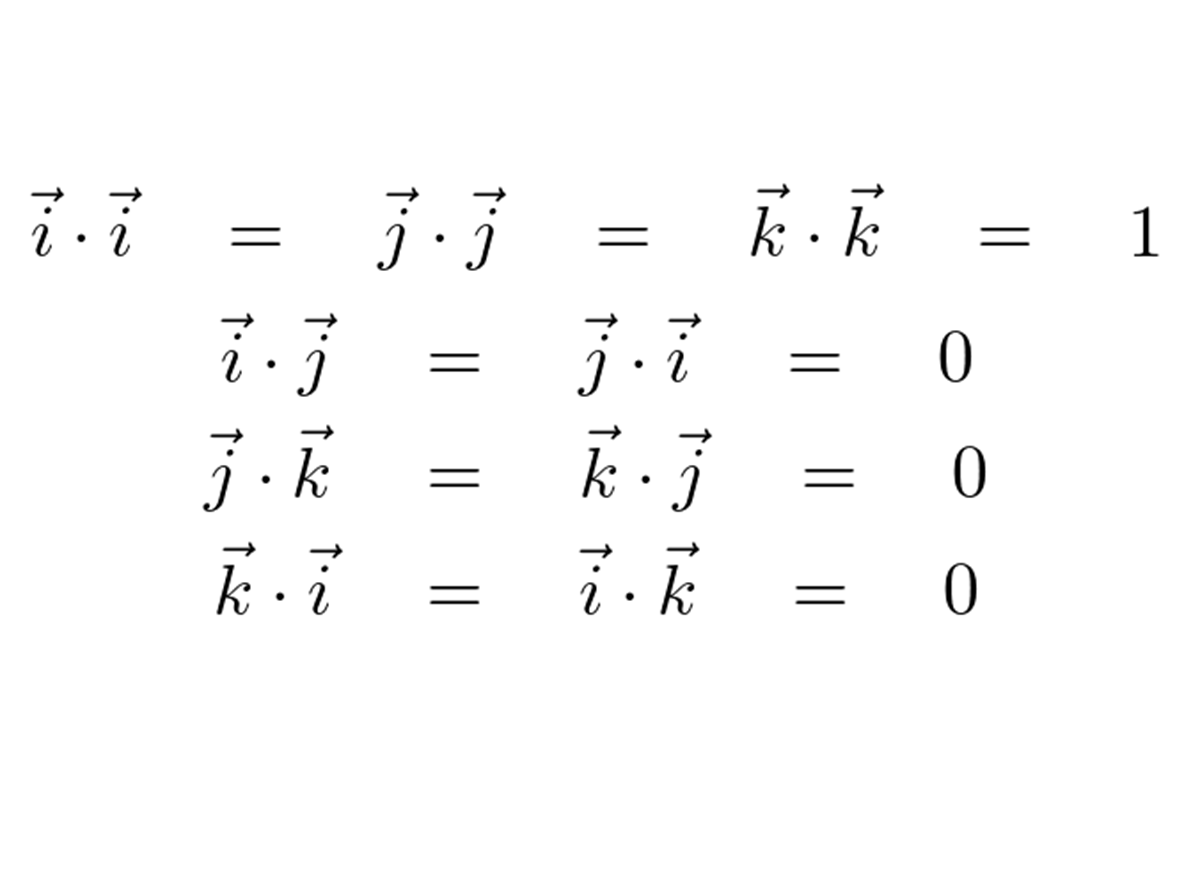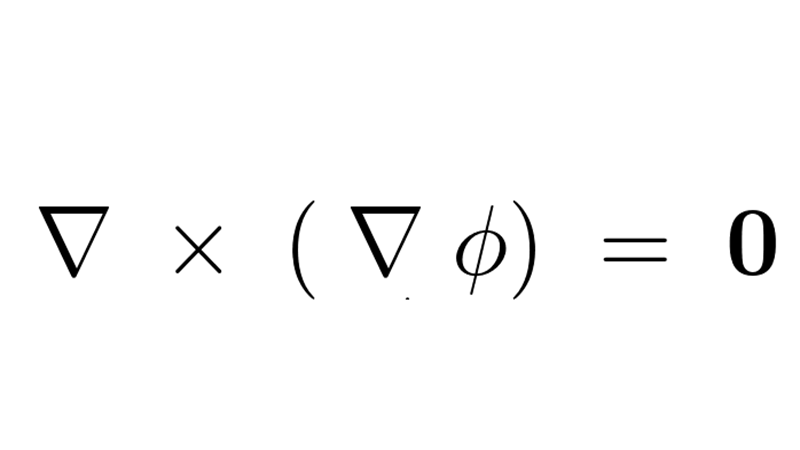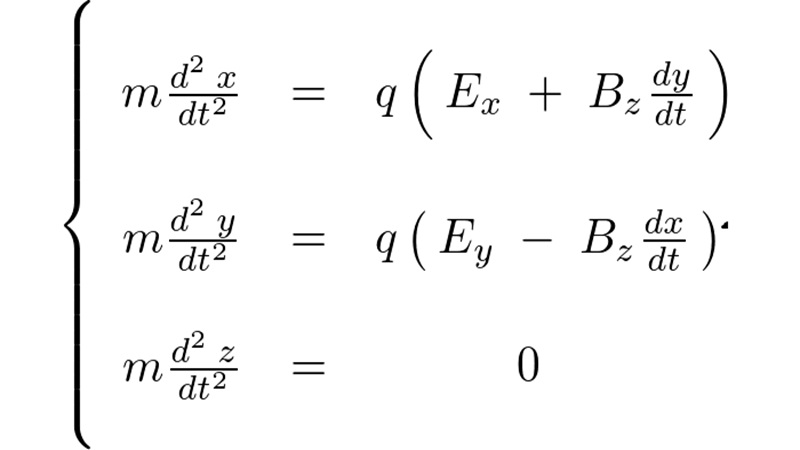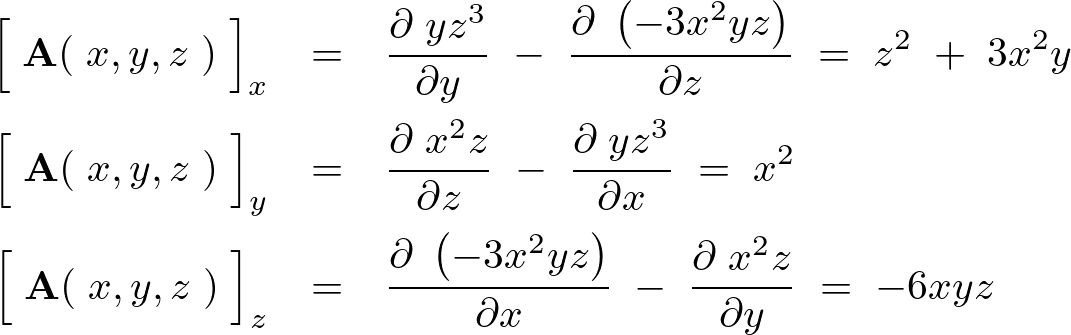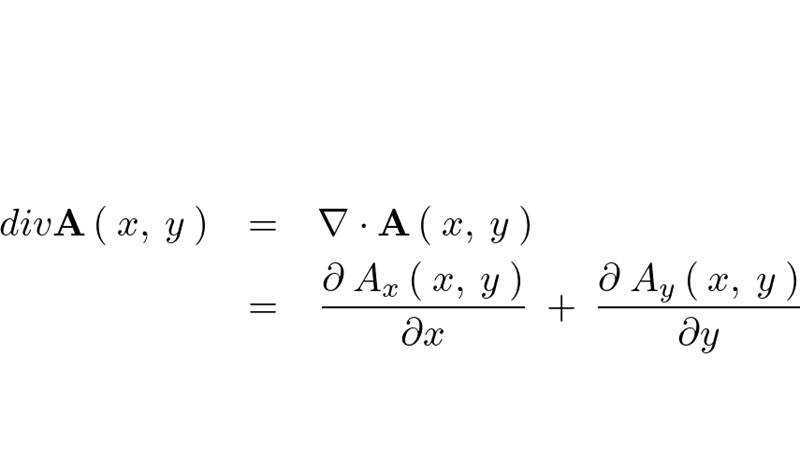平行軸定理の応用①
くり抜き円盤の慣性モーメントの導出方法
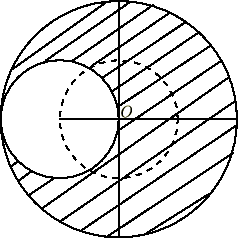
画像の左側の斜線なしの部分は、元の円盤(半径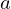 )から半径
)から半径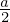 の部分をくりぬいたものと考えてください。
の部分をくりぬいたものと考えてください。
中心を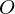 、半径
、半径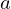 の円盤から、その半径を直径とする円をくり抜いた残りの部分の
の円盤から、その半径を直径とする円をくり抜いた残りの部分の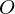 を通り、円盤に垂直な軸に関する慣性モーメントを求めます。
を通り、円盤に垂直な軸に関する慣性モーメントを求めます。
考える剛体を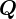 、くり抜く円を
、くり抜く円を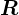 、軸を
、軸を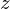 軸とし、くり抜く前の円盤剛体を
軸とし、くり抜く前の円盤剛体を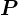 とします。
とします。
さらに円をくり抜く前の円盤の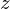 軸周りの慣性モーメントを
軸周りの慣性モーメントを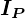 、考える剛体
、考える剛体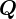 における軸周りの慣性モーメントを
における軸周りの慣性モーメントを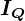 、さらにくり抜いた円盤剛体
、さらにくり抜いた円盤剛体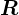 の
の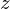 軸周りの慣性モーメントを
軸周りの慣性モーメントを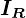 とします。
とします。
まず慣性モーメントの定義により次のような式が成り立ちます。
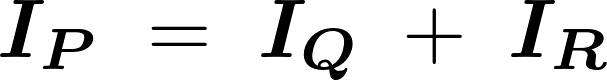
これを変形させると、
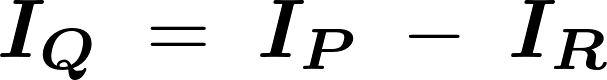
次に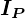 を考えます。
を考えます。
円をくり抜く前の円盤の質量を とすると今考えている円盤におけるその面積密度に関しては、
とすると今考えている円盤におけるその面積密度に関しては、

微小面積は平面極座標を使えば、

となるので、微小部分の質量は、
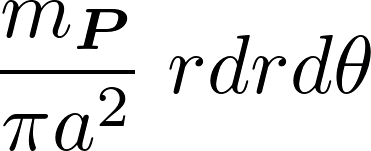
これらにより微小面積要素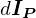 は以下のようになります。
は以下のようになります。
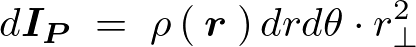
これらをもとに式を組み立てて計算していきます。

よってくり抜き前の円盤に関する慣性モーメントは以下のようになります。

次に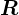 を考えます。
を考えます。
 の部分の質量は、
の部分の質量は、
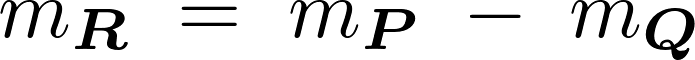
であり、この を求めるために
を求めるために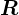 の中心を通り、
の中心を通り、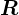 に垂直な軸周りの慣性モーメント
に垂直な軸周りの慣性モーメント を求めます。
を求めます。
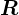 における面積密度は、
における面積密度は、
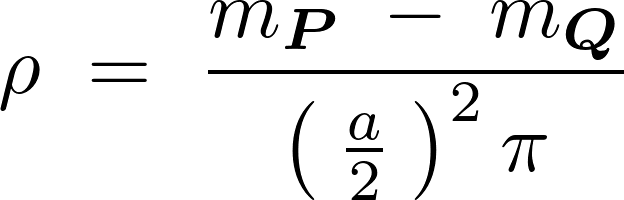
微小面積は平面極座標系を使用するのでヤコビアンは以下、
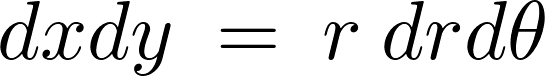
そして軸からの距離は であるので、
であるので、 の微小面積要素における慣性モーメント
の微小面積要素における慣性モーメント は以下のようになります。
は以下のようになります。

この積分式を計算していきます。
よって の慣性モーメントは以下のように求まります。
の慣性モーメントは以下のように求まります。

ここで求めたい慣性モーメントは と軸が並行で、距離が
と軸が並行で、距離が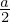 だけ離れています。
だけ離れています。
そこで平行軸の定理を使用します。
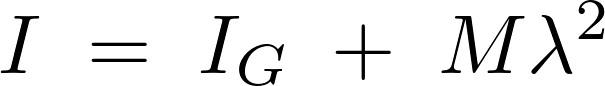
上記の平行軸の定理(シュタイナーの定理)において、左辺の求める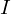 を
を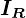 、右辺第1項の
、右辺第1項の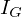 が
が に対応し、そして右辺第2項の質量に当たる
に対応し、そして右辺第2項の質量に当たる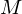 が
が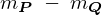 、そして同じく右辺第2項の
、そして同じく右辺第2項の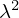 が回転軸からの距離の2乗になるので、結果、次のような式が導かれます。
が回転軸からの距離の2乗になるので、結果、次のような式が導かれます。

それぞれ代入し計算していきます。

よってくり抜いた円盤剛体の慣性モーメント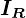 に関しては以下のように求まります。
に関しては以下のように求まります。

これらの結果により求めようとしているくり抜かれた円盤の慣性モーメント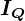 は、
は、

だったのでそれぞれに代入していって計算していきます。

これらの結果により求めようとしているくり抜かれた円盤の慣性モーメント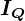 は、
は、


長方形板の慣性モーメントの導出過程 ━ 辺の長さがそれぞれ2a,2bの厚さを考えない長方形板の重心を通る対称軸に関する慣性モーメントの計算

直方体の慣性モーメントの導出過程 ━ それぞれの辺の長さを2a、2b、2cとした場合の直方体の重心を通る軸に関する慣性モーメントの計算

棒の対称軸に関しての慣性モーメントの導出過程 ━ 長さ2aの棒の中点を通り棒に垂直な軸に関する慣性モーメントの導出計算過程

棒の慣性モーメントその②の導出過程 ━ 長さ2aの細長い棒の中点を通り棒とαの角をなす直線に関する慣性モーメントの導出過程

円盤の対称軸に関する慣性モーメントの計算 ━ 半径、質量がの円盤を考えます。この円盤の中心を通りその円盤に垂直な軸の周りの慣性モーメント

円盤の慣性モーメントその② ━ 円盤の中心を通り、円盤の法線面上の垂直線とαの角をなす直線に関する慣性モーメントを求めます。

中空円盤の慣性モーメントの導出過程 ━ 中空円盤の内半径をa、外半径をbとします。こうしたときの中空円盤の慣性モーメントを求めていきます。
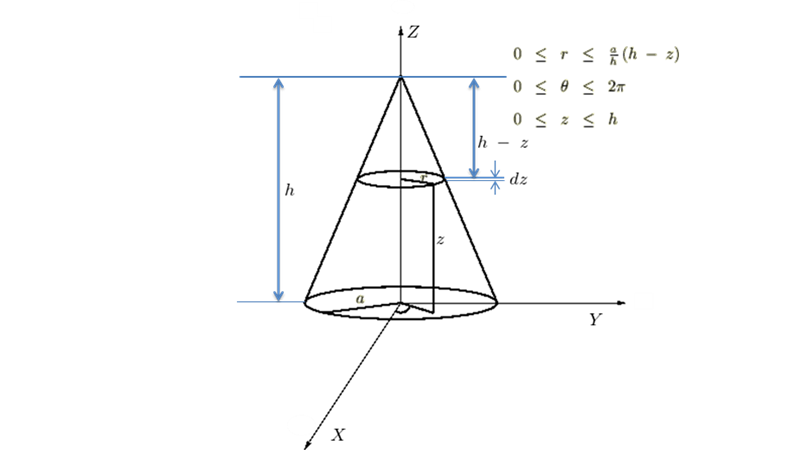
円錐の慣性モーメント ━ ある質点間の距離が変化しない円錐の頂点と、底面の中心を通るZ軸周りの慣性モーメントを求めていきます。

球の慣性モーメントの計算 ━ 球の中心部分となる重心点を通る軸に関する慣性モーメント。考える球体の質量はM、半径はRの均一な球体とします。

円輪の中心を通る対称軸に関する慣性モーメントの計算。極座標系を取り質量はM、半径はa、円周は2πnとしたときのx,y,z軸周りの慣性モーメント

一様密度で質量M、外径b、内半径aの球殻の中心を通る慣性モーメントの厚さがある場合と厚さを無視できる場合の慣性モーメントを考察していきます。

円柱の重心を通る対称軸に関する慣性モーメントの計算 ━ 半径がa、高さがlで質量がMとする円柱のxyz軸におけるそれぞれの慣性モーメント。

中空円筒の重心を通る軸に関する慣性モーメント ━ 一様密度で質量がM、半径がa、長さをlとし、円筒の外側の厚さは無視できるものとします。
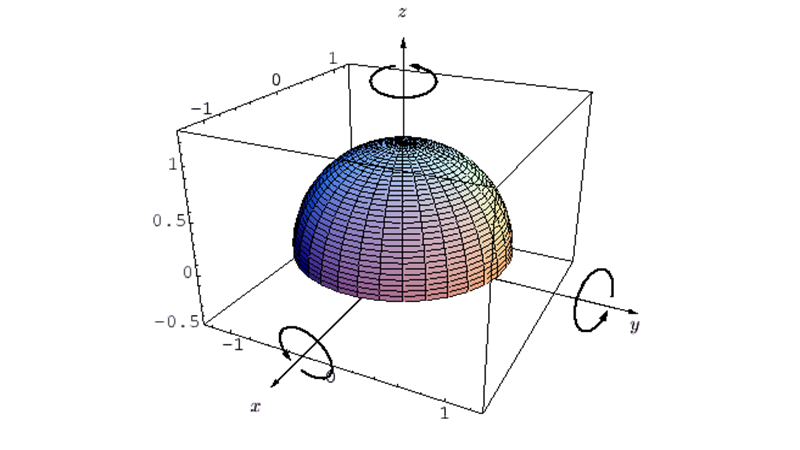
半球体の重心を通る軸に関する慣性モーメントの導出 ━ 質量がM、半径がaの半球体の重心周りに関する慣性モーメントの計算過程。

くり抜かれた円盤の慣性モーメントに関して、平行軸の定理を利用して目的とする円盤の慣性モーメントの導出に関して詳しく解説していきます。
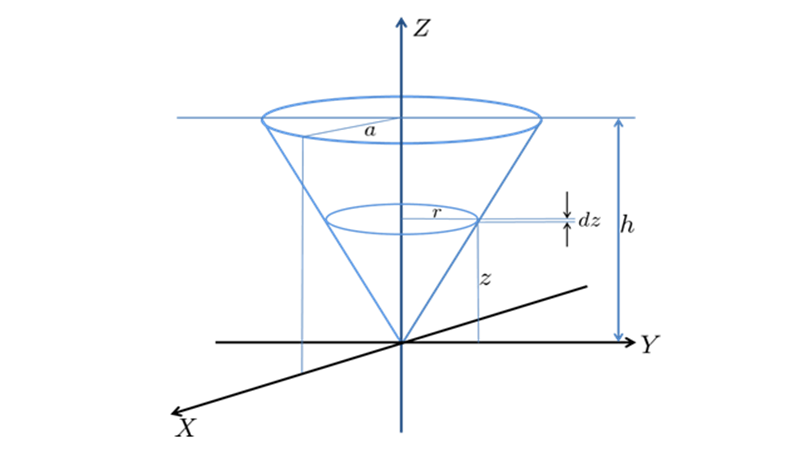
円錐の慣性モーメント-2
円錐の頂点周り、円錐底面に平行で中心点を通る軸周りの慣性モーメント、さらには円錐の重心回りの慣性モーメントについて考察していきます。
-
このセクションでは平行軸の定理を利用した円錐の頂点周り、円錐底面に平行で中心点を通る軸周りに関する慣性モーメン…
続きを読む
-
n変量のデータから得られる行列におけるn個からなる対角成分Vとn(n-1)個の共分散(Covariaence)…
続きを読む
-
平行軸の定理という物体(剛体)の物理的特性を利用しながら円錐の慣性モーメントを2つの視点から求め、また更に同じ…
続きを読む
-
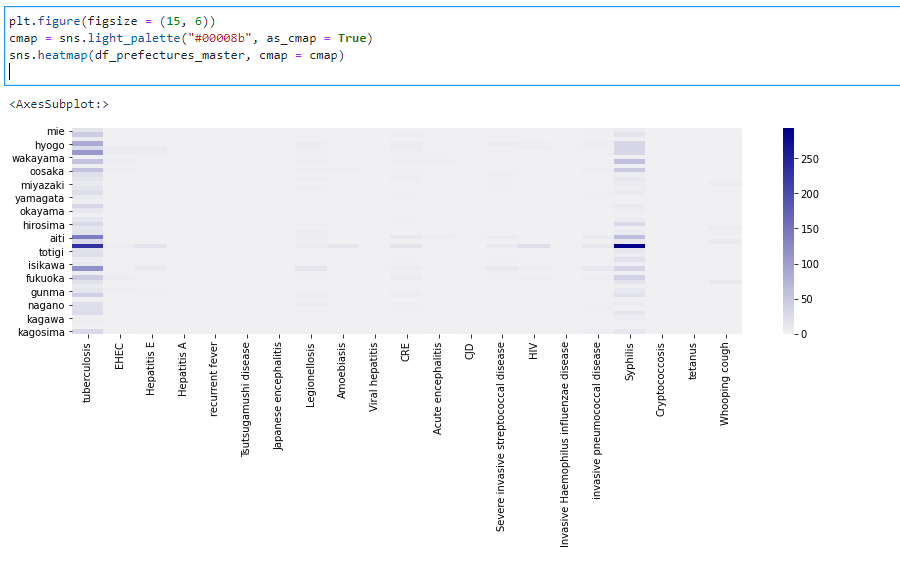
サンプルにするデータはIDWR速報データの五類感染症に関して都道府県別発生件数を週ごとにまとめられたCSVファ…
続きを読む
-
線形代数において使われた転置行列や内積の性質、および偏微分について簡単に解説していきます。
続きを読む
-
ベクトル解析においてその他重要な性質に関して簡単にまとめてみました。
続きを読む
-
今まで学んできた内容をもとに電磁気学へのその応用について考察していきましょう。
続きを読む
-
先ほどのベクトル場回転に関しての問題の答えをしていきましょう。
続きを読む
-
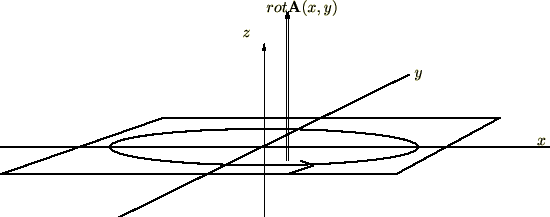
このセクションではベクトル場の回転とその意味について考察していきます。
続きを読む
-
ベクトル場の発散に関しての問題 ━ 与えられたベクトル場に関して、特定の座標点におけるそのダイバージェンスを求…
続きを読む
-
このセクションではくり抜かれた円盤の慣性モーメントに関して、平行軸の定理を利用して目的とする円盤の慣性モーメン…
続きを読む

![]() )から半径
)から半径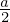 の部分をくりぬいたものと考えてください。
の部分をくりぬいたものと考えてください。 、半径
、半径![]() の円盤から、その半径を直径とする円をくり抜いた残りの部分の
の円盤から、その半径を直径とする円をくり抜いた残りの部分の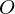 を通り、円盤に垂直な軸に関する慣性モーメントを求めます。
を通り、円盤に垂直な軸に関する慣性モーメントを求めます。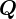 、くり抜く円を
、くり抜く円を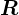 、軸を
、軸を![]() 軸とし、くり抜く前の円盤剛体を
軸とし、くり抜く前の円盤剛体を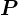 とします。
とします。![]() 軸周りの慣性モーメントを
軸周りの慣性モーメントを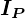 、考える剛体
、考える剛体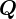 における軸周りの慣性モーメントを
における軸周りの慣性モーメントを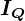 、さらにくり抜いた円盤剛体
、さらにくり抜いた円盤剛体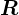 の
の![]() 軸周りの慣性モーメントを
軸周りの慣性モーメントを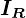 とします。
とします。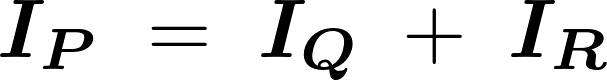
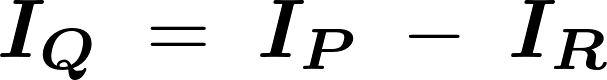
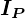 を考えます。
を考えます。 とすると今考えている円盤におけるその面積密度に関しては、
とすると今考えている円盤におけるその面積密度に関しては、

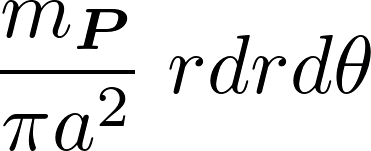
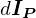 は以下のようになります。
は以下のようになります。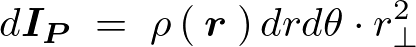


 を考えます。
を考えます。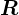 の部分の質量は、
の部分の質量は、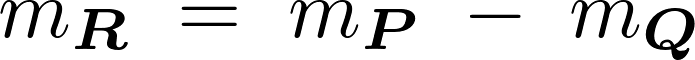
 を求めるために
を求めるために の中心を通り、
の中心を通り、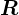 に垂直な軸周りの慣性モーメント
に垂直な軸周りの慣性モーメント を求めます。
を求めます。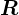 における面積密度は、
における面積密度は、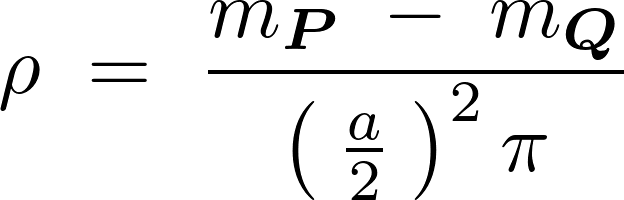
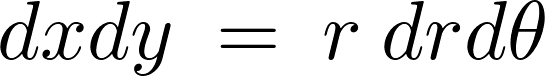
![]() であるので、
であるので、 の微小面積要素における慣性モーメント
の微小面積要素における慣性モーメント は以下のようになります。
は以下のようになります。
 の慣性モーメントは以下のように求まります。
の慣性モーメントは以下のように求まります。
 と軸が並行で、距離が
と軸が並行で、距離が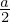 だけ離れています。
だけ離れています。
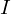 を
を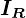 、右辺第1項の
、右辺第1項の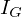 が
が に対応し、そして右辺第2項の質量に当たる
に対応し、そして右辺第2項の質量に当たる![]() が
が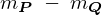 、そして同じく右辺第2項の
、そして同じく右辺第2項の![]() が回転軸からの距離の2乗になるので、結果、次のような式が導かれます。
が回転軸からの距離の2乗になるので、結果、次のような式が導かれます。

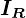 に関しては以下のように求まります。
に関しては以下のように求まります。
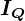 は、
は、

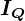 は、
は、