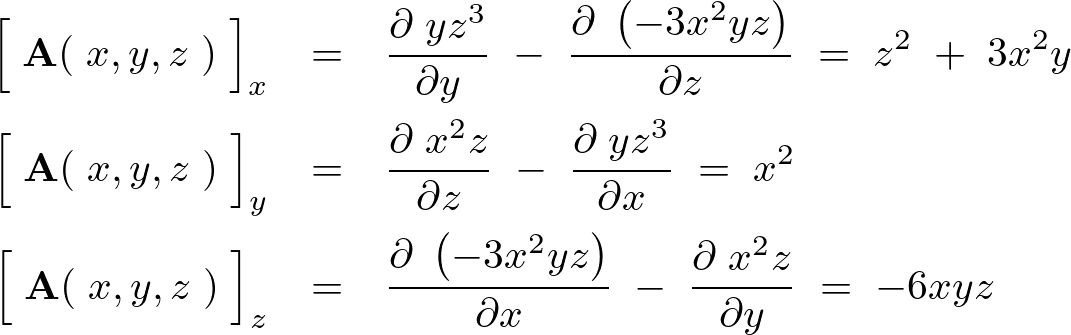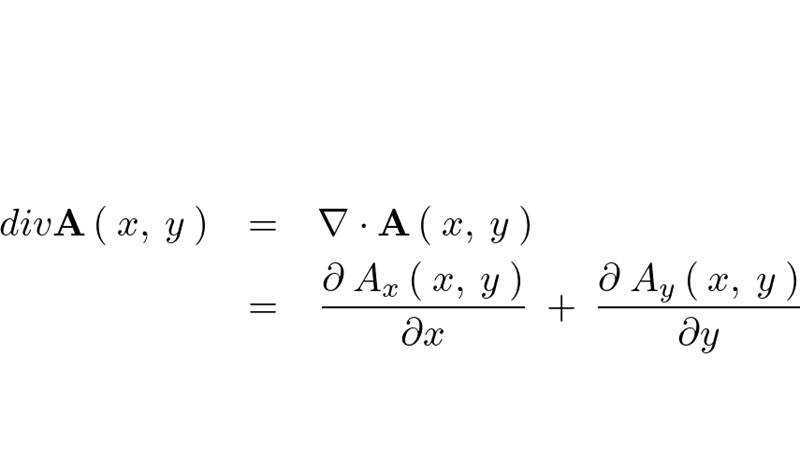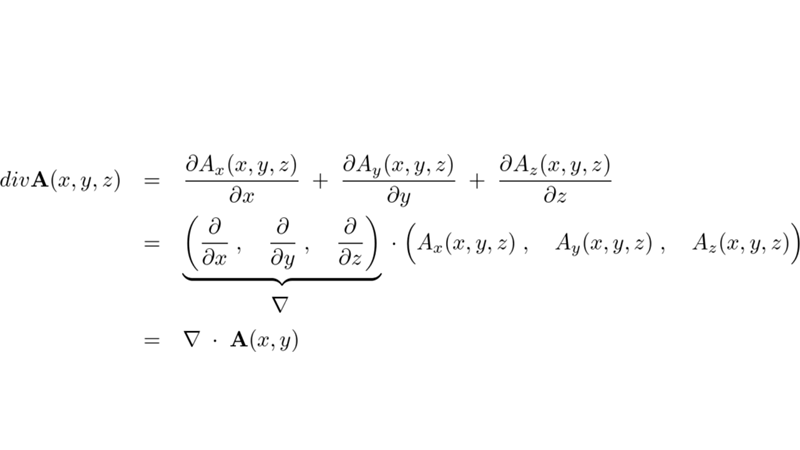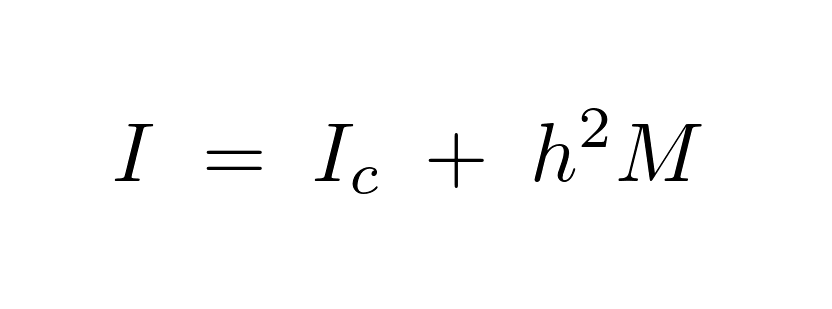平行軸の定理と慣性モーメント
このチャプターは“平行軸の定理”で学習した内容の応用編になります。
平行軸の定理とは、物体の軸に関しての慣性モーメントがわかっているとき、これに平行な位置における軸に関しての慣性モーメントを求めるとき使われる計算法になります。
平行軸の定理に関してのおさらい
任意の点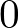 を通る
を通る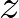 軸の周りの慣性モーメントの計算
軸の周りの慣性モーメントの計算
重心を通る1つの軸があるとし、それを![]() 軸として、
軸として、![]() 軸の周りの剛体の慣性モーメントを
軸の周りの剛体の慣性モーメントを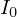 とします。
とします。
この軸に平行で![]() の距離を隔てた軸まわりの慣性モーメントを考えると、
の距離を隔てた軸まわりの慣性モーメントを考えると、

の式を積分の形にすれば、
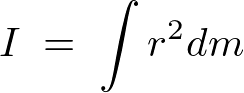
 点の
点の の周りのモーメントは、
の周りのモーメントは、
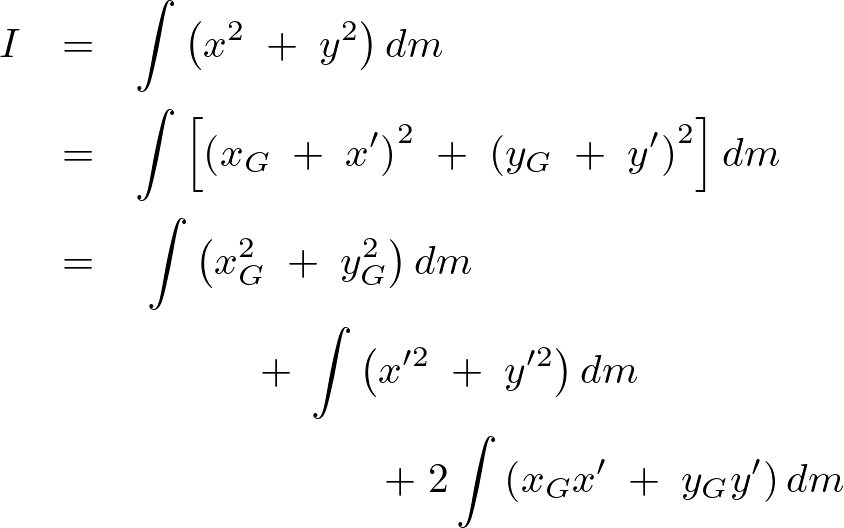
ここで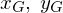 を質量中心の座標とします。
を質量中心の座標とします。
積分の第2項は質量中心を通り、![]() 軸に平行な軸周りの慣性モーメントであり、これを
軸に平行な軸周りの慣性モーメントであり、これを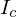 とします。
とします。
質量中心より回転の中心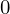 までの距離を
までの距離を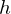 とすると、
とすると、
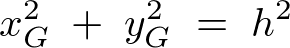
さらに第3項の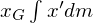 、および
、および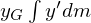 は質量中心の定義においてゼロ。
は質量中心の定義においてゼロ。
以上の結果より、慣性モーメントとして、
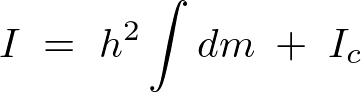
すなわち、

が導かれることになります。
このチャプターではこの平行軸の定理を利用した応用編となっています。

くり抜き円盤の慣性モーメント
くり抜かれた円盤の慣性モーメントに関して、平行軸の定理を利用して目的とする円盤の慣性モーメントの導出に関して詳しく解説していきます。
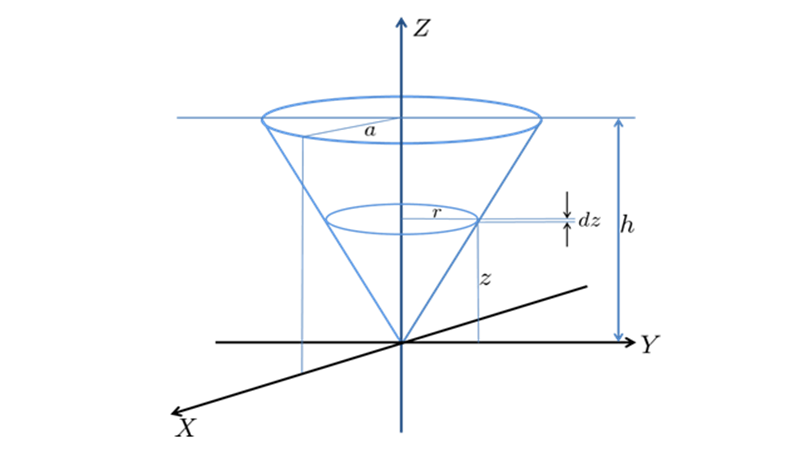
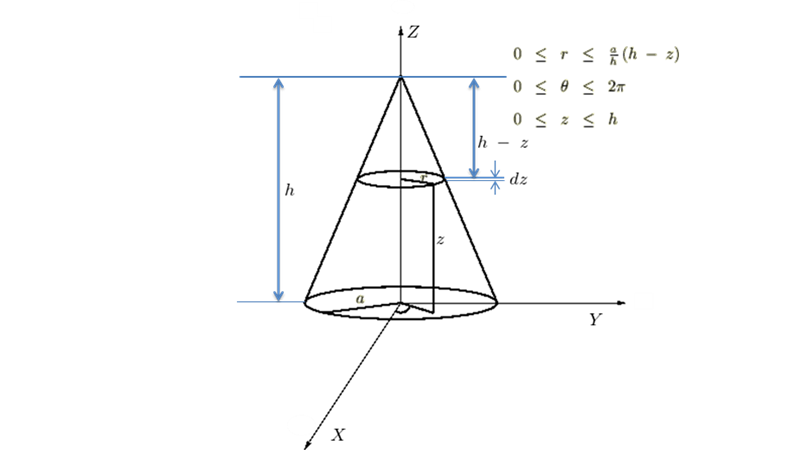
円錐の慣性モーメント-2
円錐の頂点周り、円錐底面に平行で中心点を通る軸周りの慣性モーメント、さらには円錐の重心回りの慣性モーメントについて考察していきます。
-
-
-
-
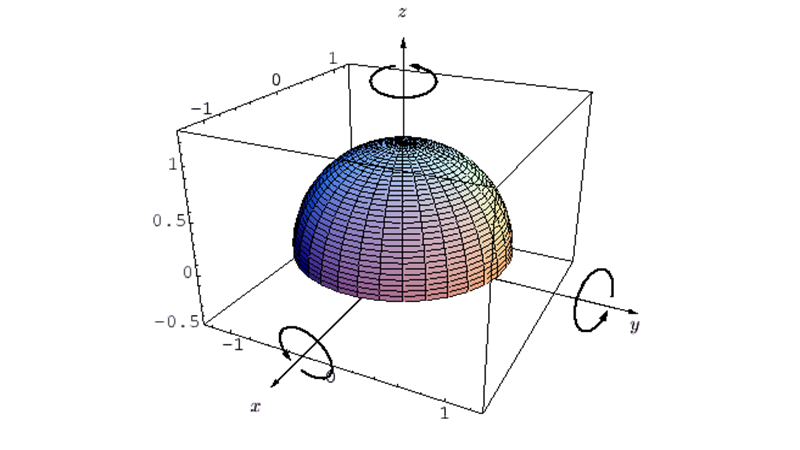
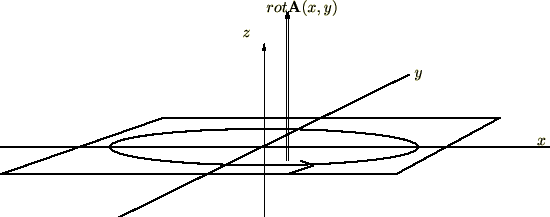
三次元ベクトル場および発散についての補足
カテゴリー : 三次元ベクトル場、発散についての補足三次元ベクトル場の発散(ダイバージェンス)に関して、ナブラとベクトル場の内積との関係について考察してみましょう…
-
-
-
-
-
-
コリオリ長距離弾道軌道計算②
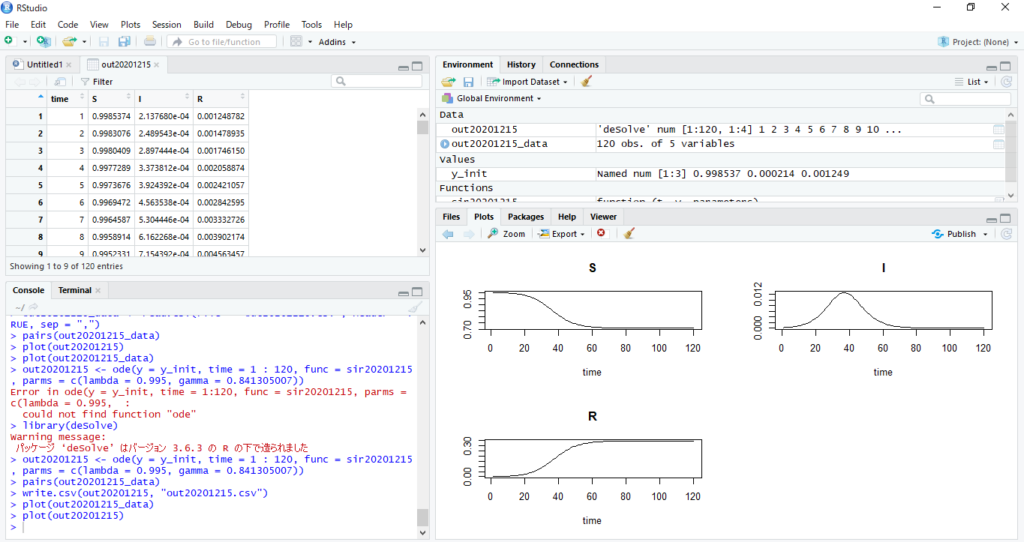
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。

-
円錐の頂点、底面、重心に関する慣性モーメント
カテゴリー : 円錐の頂点、底面、重心周りの慣性モーメントこのセクションでは平行軸の定理を利用した円錐の頂点周り、円錐底面に平行で中心点を通る軸周りに関する慣性モーメン…
-