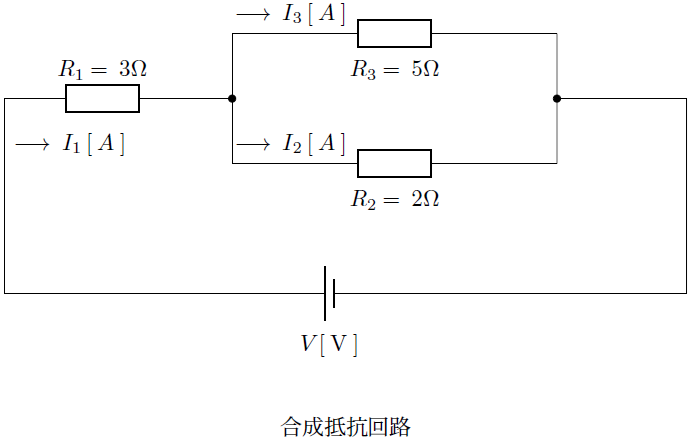
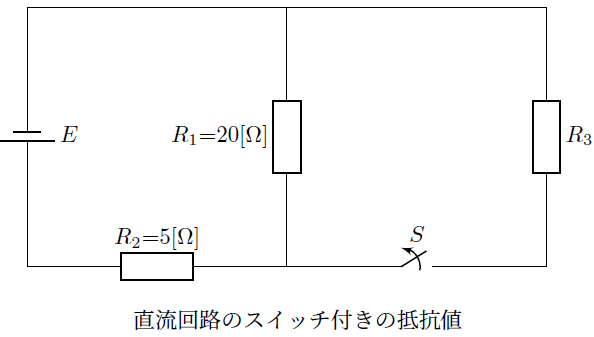
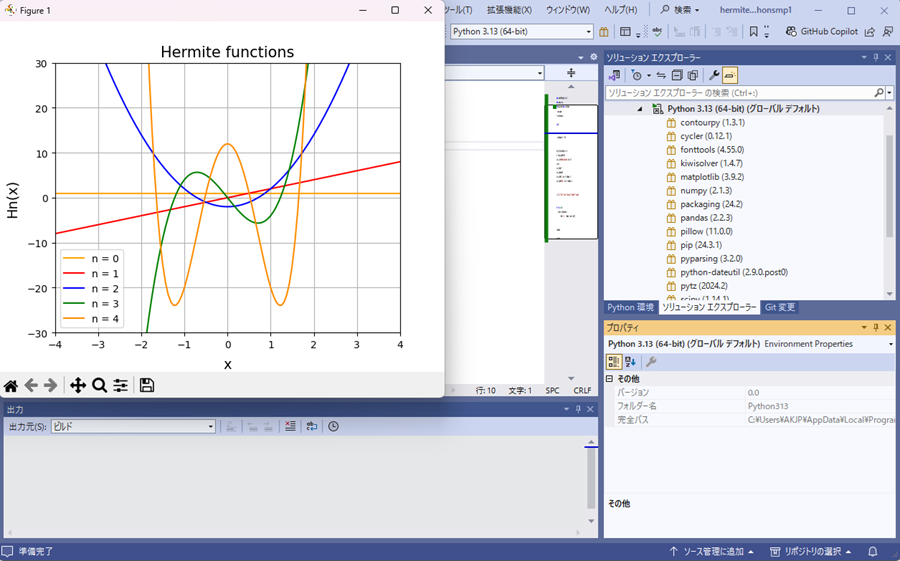
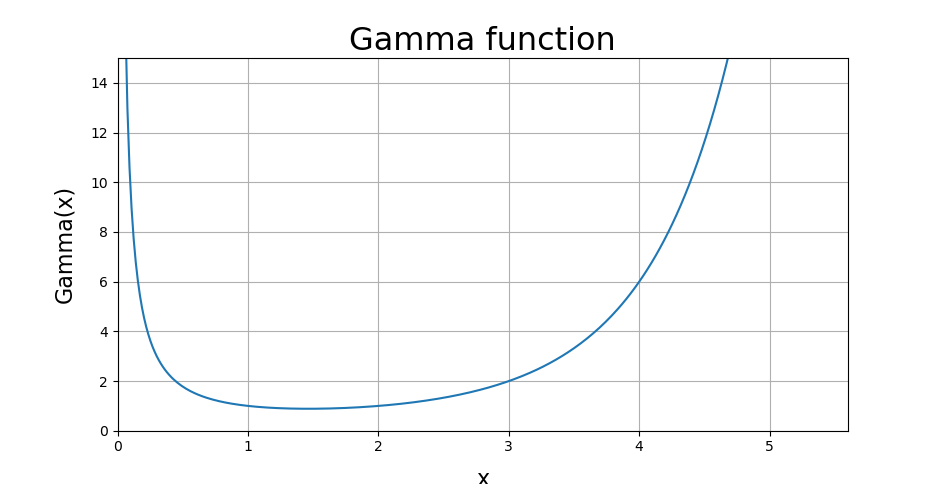
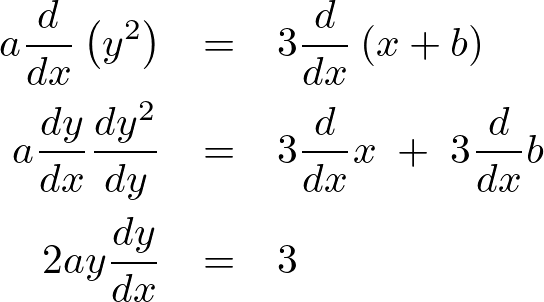規格化とは
先ほど上記に示したコンテンツおいては、例えば、
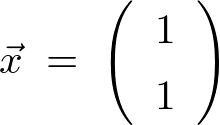
に関しては、
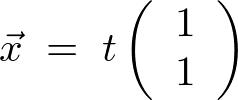
(![]() は
は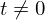 の複素数)とするのが本当は正しいのですが、
の複素数)とするのが本当は正しいのですが、
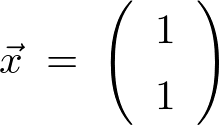
のように1つだけが代表させても特に問題はないと思います。
物理学(量子力学)において「規格化された固有ベクトルを求めなさい」という問題のときには、ベクトルの大きさを“1”にしておきます(詳しくは量子力学のテキストを参考にしてください)。
今の場合だと、
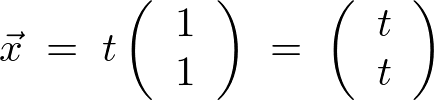
として、
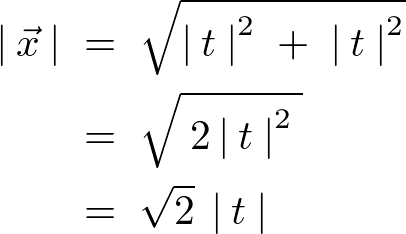
これを“1”とおきます。
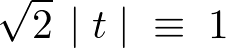
これにより、
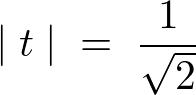
となります。
さらにこれも一般的に一つだけ代表して次のようにします。
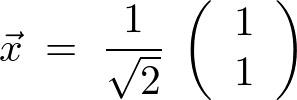
これにより、
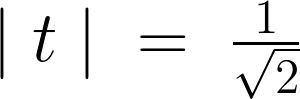
となります。
さらにこれも一般的に一つだけ代表して次のようにします。
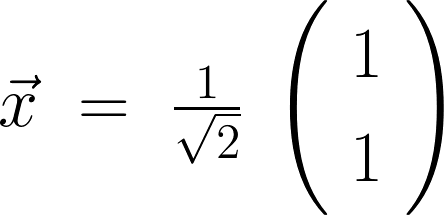
-
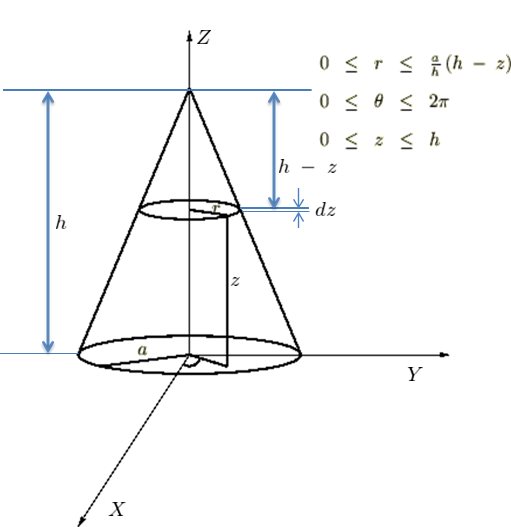
円錐の慣性モーメント
カテゴリー
-
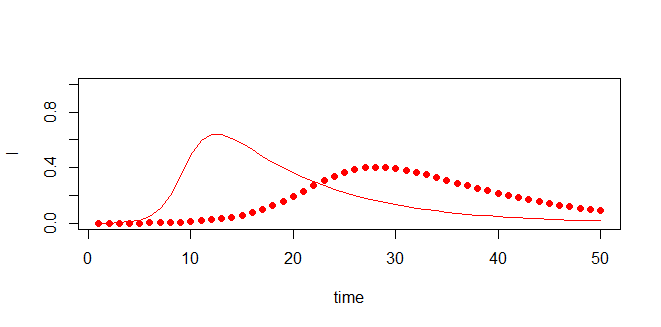
感染率による感染者数増加の比較
カテゴリー
-
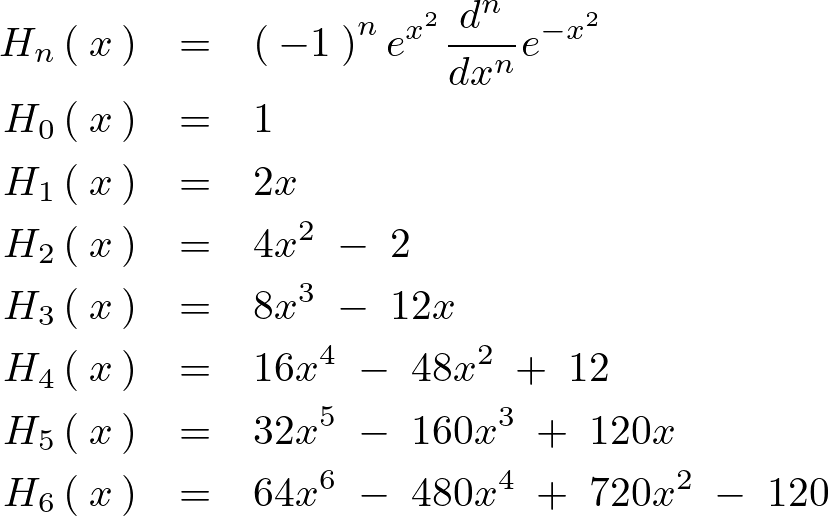
LaTeXコードの組み方
カテゴリー
-
変分原理
カテゴリー
-
ラグランジュ関数
カテゴリー
-
一階常微分方程式
カテゴリー
-
微分方程式いろいろTOPページLaTeXコード
カテゴリー : 微分方程式いろいろLaTeXコードサテライトサイト微分方程式いろいろコンテンツトップページに使われたコードになります。コンパイル時のエラー等の修…
-
-
Cisco Packet Tracer
カテゴリー : Cisco Packet TracerPacket Tracerとは、Ciscoが提供するCisco製のルータやスイッチなどをローカル端末上でコンフ…
-
-
-
-
-
-
-


 の式を計算していきます。
の式を計算していきます。