行列式を使った連立方程式の解き方
クラメル公式による解法
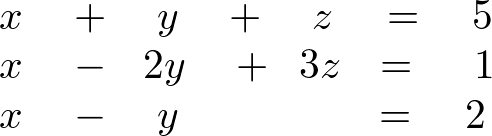
この連立方程式の行列表現は、
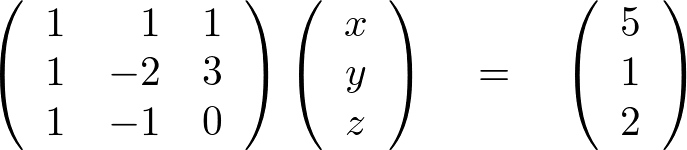
となるのがわかると思います。
これをクラメルの公式にそれぞれ当てはめて行きましょう。
ここにクラメールの公式を入れる
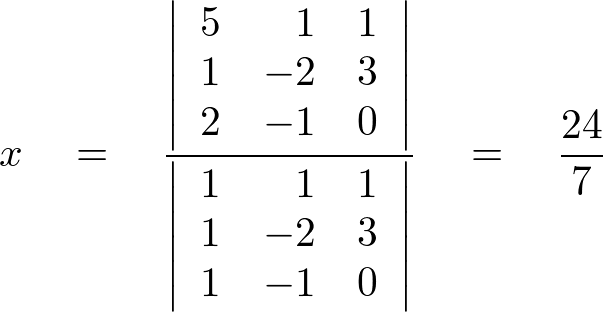
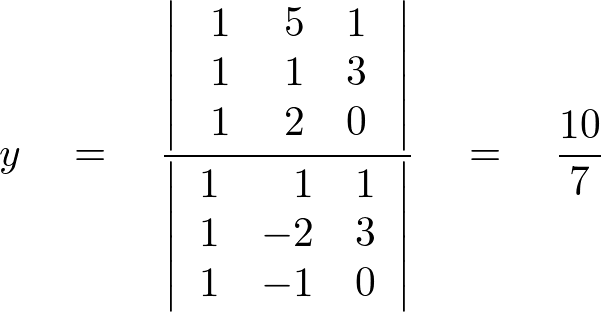
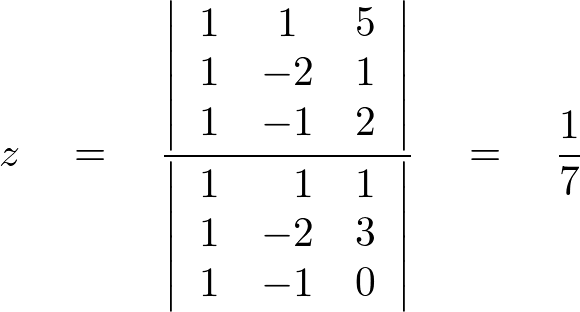
このように線形代数の初歩というのはほとんどが計算法で占められています。最初のころは難しくてこんなのだめだと思いがちですが、わかってしまえばこんなに簡単で、しかも非常に役に立つ便利な数学だということがお分かりいただけたかと思います。
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。

