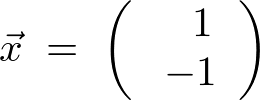固有値と固有ベクトル
考え方としては以下のようになります。
まずあるベクトル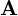 があってそれは
があってそれは![]() 行
行![]() 列の行列の(一般的には)線形演算子(一次変換)とし、また、
列の行列の(一般的には)線形演算子(一次変換)とし、また、![]() を
を![]() 次の列ベクトルとします。するとこのとき、
次の列ベクトルとします。するとこのとき、
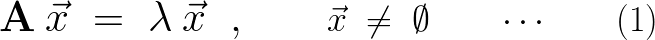
が成り立つならば、

といいます。
ちなみに量子力学においては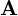 が物理量、
が物理量、![]() が状態に、
が状態に、![]() が観測される値に対応します。
が観測される値に対応します。
上記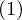 式を変形させると、
式を変形させると、
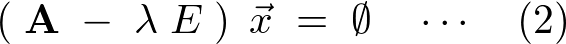
![]() は単位行列です。
は単位行列です。
今仮に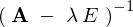 が存在したとすると、これを
が存在したとすると、これを の左から両辺にかけると、
の左から両辺にかけると、
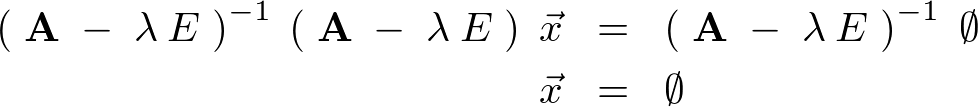
これは、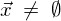 という条件に反するので
という条件に反するので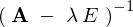 は存在しないことになります。
は存在しないことになります。
従って、
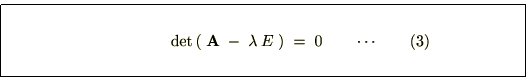
でなければなりません。
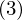 は
は![]() の
の![]() 次方程式(これを固有方程式といいます)となるのでこれを解けば固有値
次方程式(これを固有方程式といいます)となるのでこれを解けば固有値![]() が求まるという寸法になります(一般的には
が求まるという寸法になります(一般的には![]() 個求まります)。
個求まります)。
固有値![]() が求まったら、それらをそれぞれ
が求まったら、それらをそれぞれ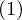 に代入し、連立方程式の形にして、そしてこれを解けば固有ベクトルが求まります。
に代入し、連立方程式の形にして、そしてこれを解けば固有ベクトルが求まります。
固有値と固有ベクトルを求める例題
固有値と固有ベクトルの例題
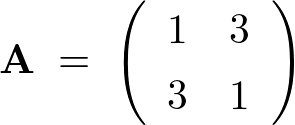
の固有値と固有ベクトルを求めてみましょう。

また、
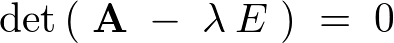
なので、次のようにそれぞれを代入していきます。
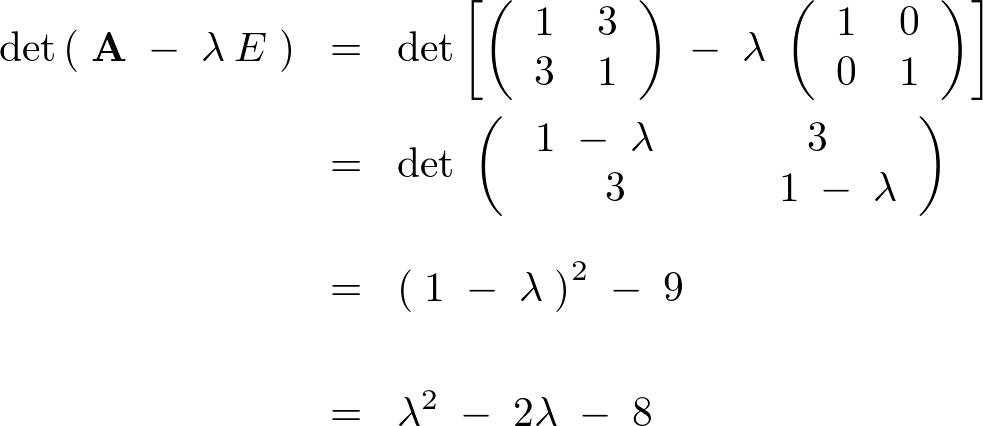
この結果により![]() は以下のように求まります。
は以下のように求まります。
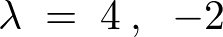
さらにここで、
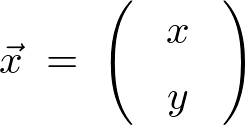
とします。
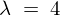 の場合
の場合
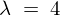 を
を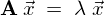 に代入して
に代入して
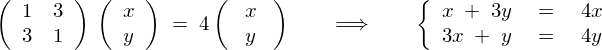
これを満たす、
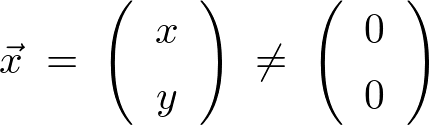
を見つけると、
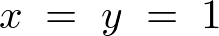
したがって、
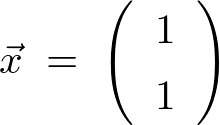
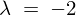 の場合
の場合
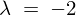 を
を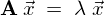 に代入します。
に代入します。
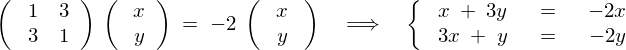
これらを満たす![]() を見つけると、
を見つけると、

になります。
なので、
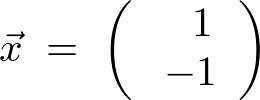
以上の結果から、
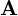 の固有値
の固有値
![]() の固有値は、
の固有値は、
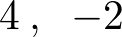
固有値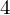 に属する固有ベクトル
に属する固有ベクトル
![]() に属する固有ベクトルは、
に属する固有ベクトルは、
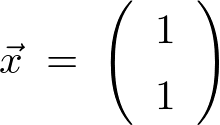
固有値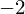 に属する固有ベクトル
に属する固有ベクトル
固有値![]() に属する固有ベクトルは、
に属する固有ベクトルは、