行列式
行列式とは
行列式の計算
サラス法と行列式展開法
一般的な線形代数学のテキストにおいては3行3列の行列式計算はサラスの方法を用いて説明しているものがほとんどだと思います。しかしこの方法は基本的にやりにくく、そして汎用性がありません。 そこでこのサイトで進めるのが行列式展開法です。この方法を使えば4行4列でも5行5列(かなり面倒になりますがちゃんと計算できます)でも計算できるようになります。
行列式展開法
次に示す式をよく見てみましょう。
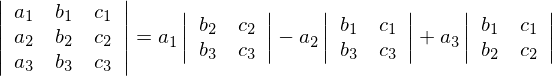
右辺![]() の真横に位置している行列式は、元の左辺の
の真横に位置している行列式は、元の左辺の![]() がある位置から6時方向と3時方向にラインを引いたとすると、そのライン上にない部分を抜き出していることがわかります。
がある位置から6時方向と3時方向にラインを引いたとすると、そのライン上にない部分を抜き出していることがわかります。
そして![]() は12時、6時方向(上下方向)と3時方向のライン、さらには
は12時、6時方向(上下方向)と3時方向のライン、さらには![]() は12時方向と3時方向のライン上にない部分を抜き出しているのがわかると思います。
は12時方向と3時方向のライン上にない部分を抜き出しているのがわかると思います。
ここで注目すべき点は符号です。
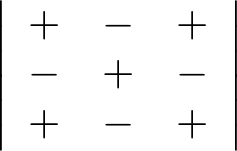
のようにプラスとマイナスを交互にして番地のように憶えましょう。4次、5次さらにはそれ以上でも同じです。 それでは早速問題を解いてみましょう。
問題
問題①
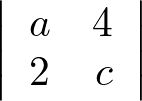
問題②
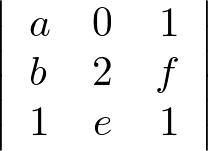
問題③
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。

