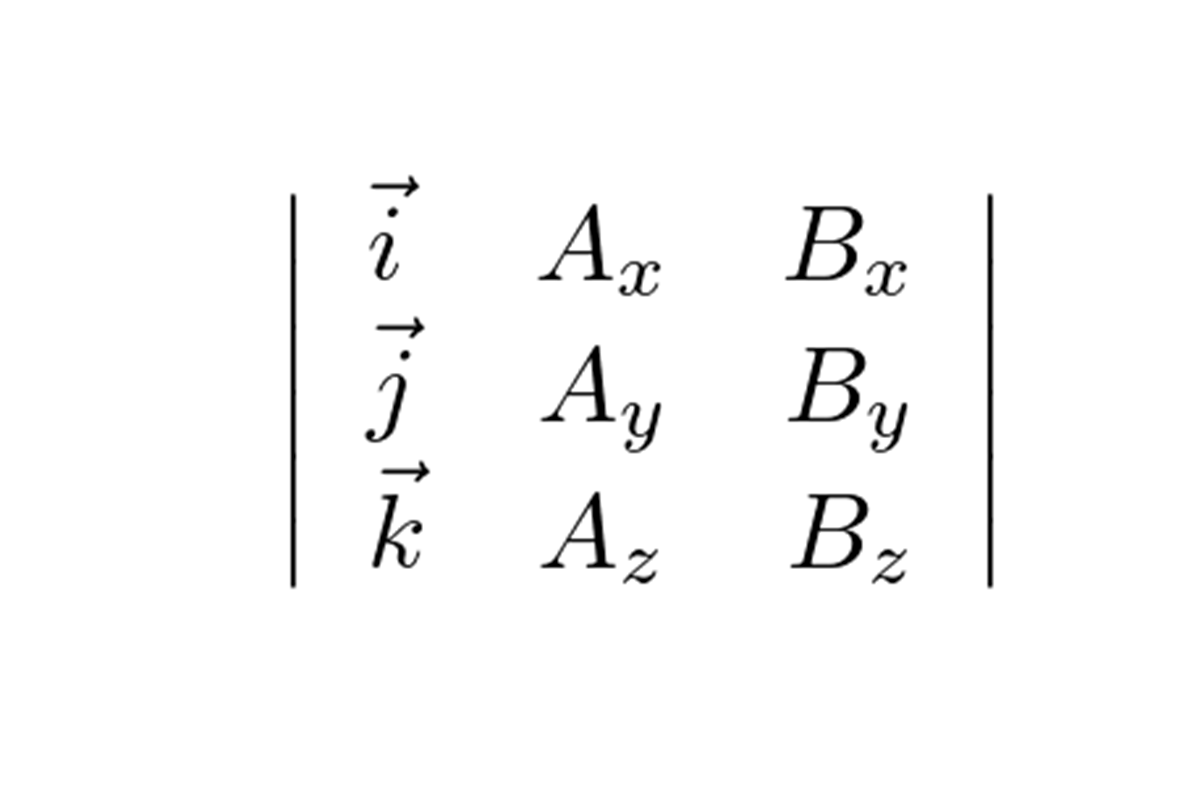ベクトル外積-Cross Product
ベクトル場の回転とは
物理科の一年次に習うベクトル解析において、

はほとんどのテキストでは3行3列の行列式に表記していると思います。
たいていの場合、実際の計算ではサラスで解くか、あるいは行列表記ではないこの公式のようなものを暗記している場合もあるかと思います。
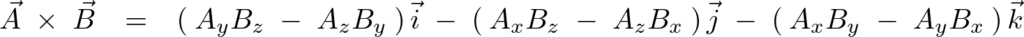
このベクトル積を行列式展開法で解いていきます。
式の変形
ベクトル積(CrossProduct)の行列式の表記はこのようだったと思います。
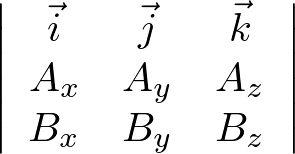
オペレートする作用素を左側に置くといった形にすれば、
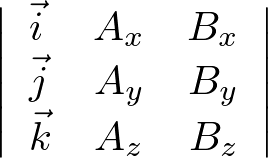
このようにすれば先ほどの行列式展開法の定義がそのまま使えます(変形せずに行列式展開法の定義でそのまま計算したとしても結果は同じです)。
早速やってみると、
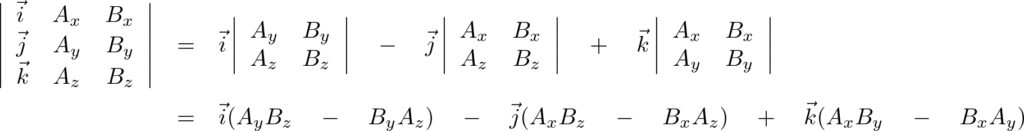
となります。
次は実際にベクトル外積の計算をしてみましょう。
問題
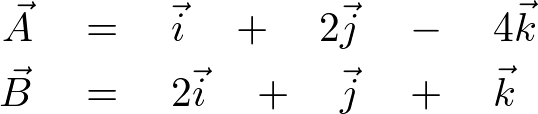
とした場合の次の外積の計算をしてみましょう。

答え
代入していって計算していきます。
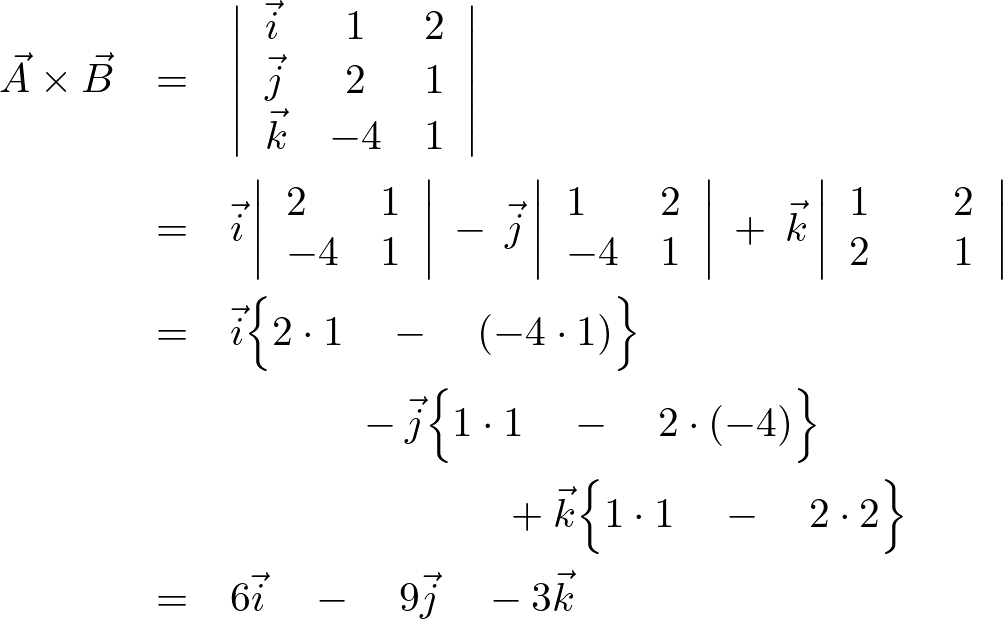
よって答えは以下のようになります。
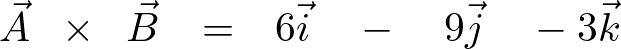

ベクトル場の回転
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

ベクトル外積
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.