物理応用線形代数
応用に関する線形代数の内容になります
ベクトル場の回転(ROT)
3次元方向の要素を持ったあるベクトル![]() を次のように考えます。
を次のように考えます。
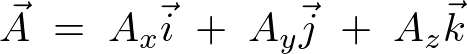
これに対し、次のようなベクトル場、
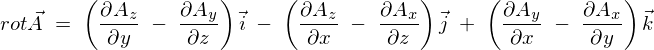
と表されるベクトル場を回転、またはローテーションといいます。
ベクトル場の外積(クロスプロダクト)
さらにベクトル場![]() を、
を、

としたとき
これを次のように置きます。

このようにあらわすとき、上記2つの外積式は次のようになります。
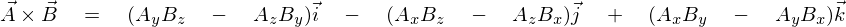
次のチャプターではこれらについての説明になります。
よいこの低学年向けすうがくひろば
3次元方向の要素を持ったあるベクトル![]() を次のように考えます。
を次のように考えます。
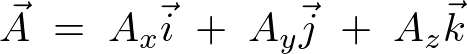
これに対し、次のようなベクトル場、
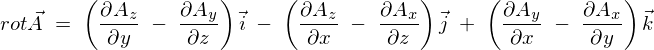
と表されるベクトル場を回転、またはローテーションといいます。
さらにベクトル場![]() を、
を、

としたとき
これを次のように置きます。

このようにあらわすとき、上記2つの外積式は次のようになります。
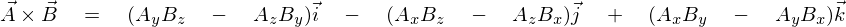
次のチャプターではこれらについての説明になります。