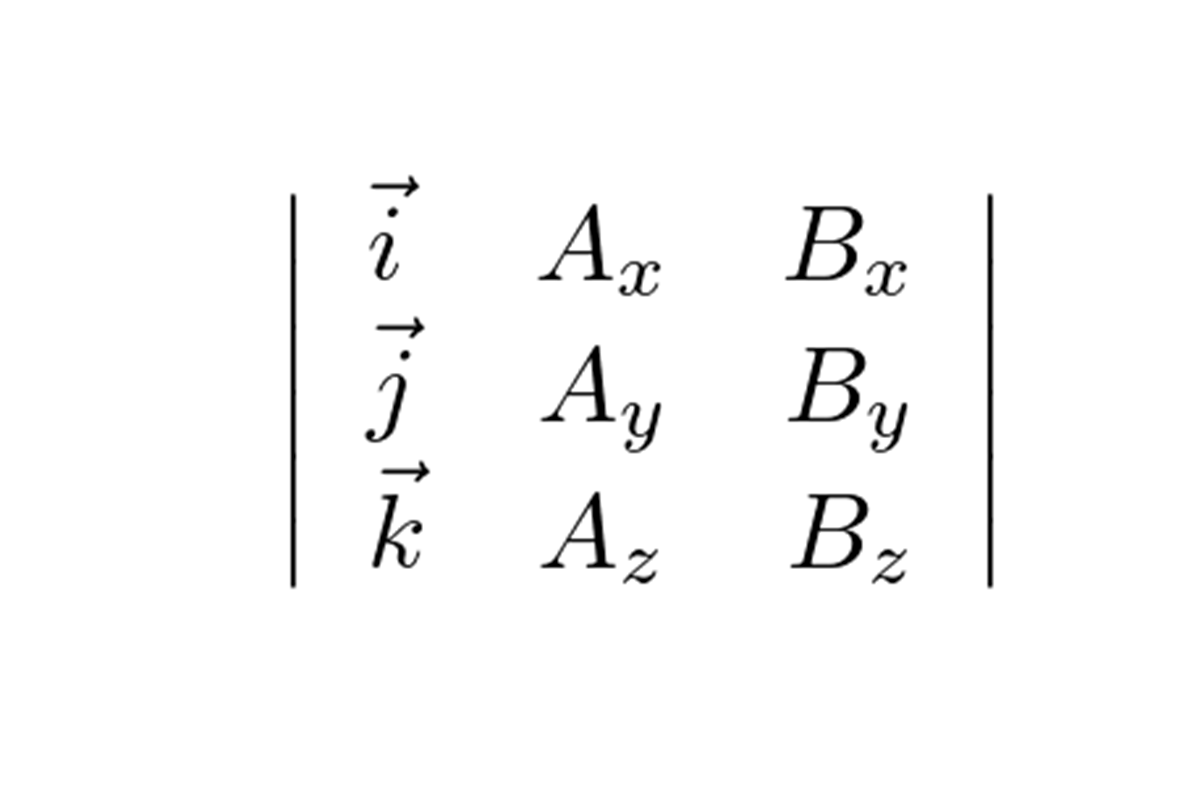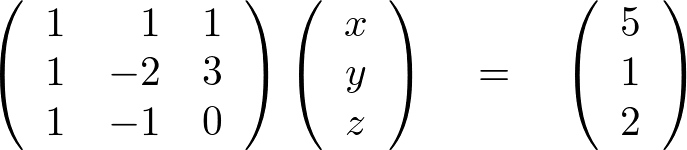第0章━線形代数学の基本的概念
線形代数学というのは現代科学に携わるものたちにとって好き嫌いに関係なくその技術・領域の知識は理論物理学においていたるところにでてきます。にもかかわらず大学の２・３年次、それどころか卒業する時点に至っても線形代数学において基本であるはずの行列及び行列式や逆行列の計算がまともに計算できないという学生がいます。
これは講師の責任もあるのでしょうが恐らくは授業の中で一般的に教わっているサラス法に問題があるのではないかと考えています。このサイトではそのサラス法によらない行列式（ｄｅｔｅｒｍｉｎａｎｔ）の解法（行列式展開法）を示します。この方法を身につけることによってrot計算やCross Product（ベクトル外積）の計算が向上（公式を記憶する必要がありません）するばかりでなく、行列式の４次、５次の計算も効率的にできるようになります。
線形代数学の使い道
－ もともとは連立方程式をシステマティックに解く技術から出発したものです。しかし現在の物理学にいたっては相対論や力学、さらには量子力学といった分野でその威力を発揮するものです。線形代数学という分野が現代の物理学において、空間を語るための言語といわれる所以は実はここにあります。
行列と行列式
言葉は非常に似ていますが基本的に違うものになります。
あんパンにはあんが入っており、ジャムパンにはジャムがはいってます。だけどうぐいすパンには鶯入ってない－それぐらいの開きがあります。
例）３行３列の行列
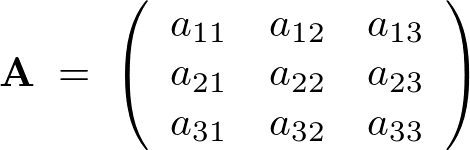
横方向の並びの数字（要素）を“行”、そして縦方向の並びにおける数字（要素）を“列”といいます。 このようにｍ行ｎ列で並べたものをｍ行ｎ列行列などといったりします。
上記の例ではｍ＝ｎになっていますがｍ≠ｎの場合もあります。 例えば次に示す連立方程式、
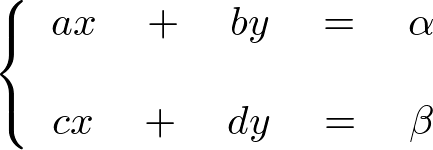
は行列を使うと次のように表現できます。
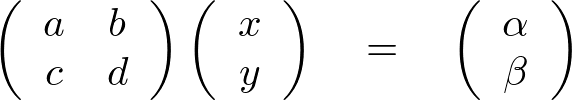
一般的にベクトル
の第
行から取り出した、
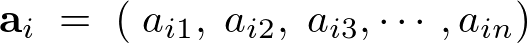
なるものを行ベクトル、また同じくベクトルの第
列から取り出した、
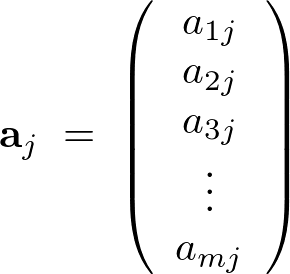
を列ベクトルといいます。
例えばの第1行ベクトルは、
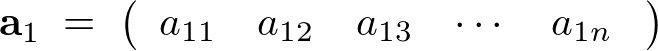
また、の第１列ベクトルは、
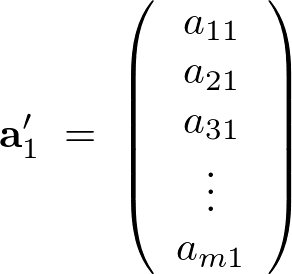
そしてこの行列に対し、行列式（determinant）はｎ個の要素の２乗、つまり正方行列（行の数と列の数が同じ行列のこと）に対して定められる量です。
書き方としては次のようになります。
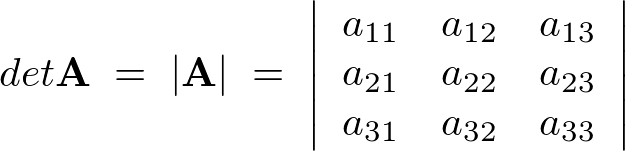
またある正方行列において次のようなもの、
このような対角成分がすべて１で、その他の成分がすべて０で成り立つものを単位行列といい一般的に
で表現します。
具体的な計算―行列の計算
まずは自力で計算をしてみましょう。たとえわからなくともまず実行することが大事です。
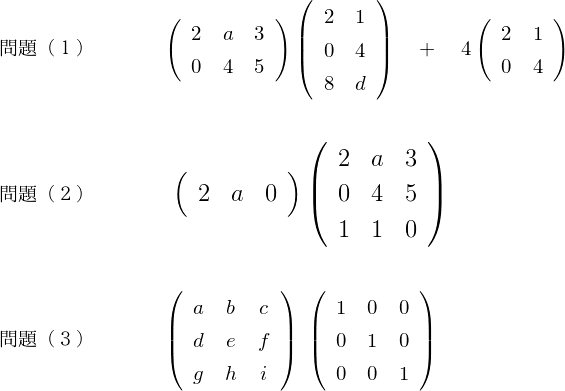
答え
それぞれの問題の対応している数字に着目してみましょう。
問題①
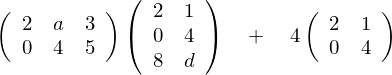
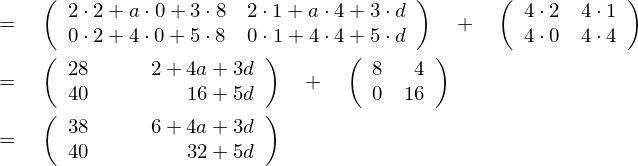
＋より左側の２つの括弧の計算の説明
コツはヨコ（左括弧の中）→タテ（右括弧の中）、ヨコ（〃）→タテ（〃）…、の繰り返しによる掛け算です。
左の括弧の中の数字は“左から右へ”、右側の括弧の中の数字はは“上から下へ…”、の順番の繰り返しです。ヨコ－タテ法として覚えましょう。こればかりは習うより慣れるしかありません。
＋より右側の括弧の計算の説明
スカラー倍です。それぞれの数字に４を掛けただけです。
問題２
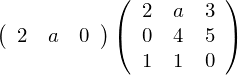
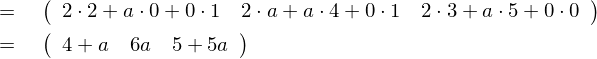
※注目すべきは、１行３列と３行３列を掛け合わせたものは“１行３列”になるということです。
わからない場合はよくみてじっくり考えてみましょう。 こういったものはまず習うより慣れることが大事です。
問題３
左辺右側にある行列は先ほど述べた単位行列です。
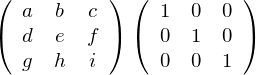
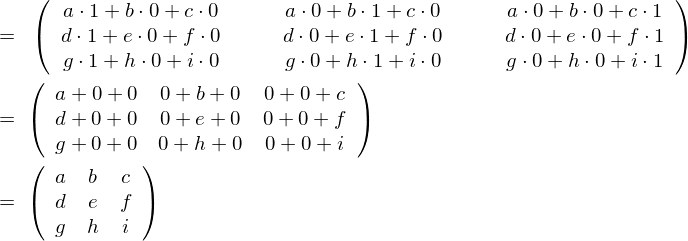
このサイトの対象者
- 主に大学の物理学科一年生を対象としていますがその他の学部の方に対しても有効です。または社会人でAIエンジニアやデータ解析者などの職業の方でこれから線形代数の基礎を学びたい方という方でも大丈夫でしょう。さらには高校生でもかまいません。たとえ高校生でも優秀な学生さんならば（おそらく数十分で）十分に理解できることと思います。
- 学習方法としては特にどうしろとは言いません。ご自分でやりやすいようにやってください。ただし一つアドバイスするならばやはり紙とペンをとって自分の手を動かして計算することを強くお勧めします。 ページの進め方としてはプルダウンから入る場合は上から下への順番で進むといった形になります。
ページの進め方は最下部にあるNEXTボタンを押していけば順通りにページが進んでいく仕組みになっています。