交流回路の直列接続
交流回路の直列接続
RL直列回路
以下のような抵抗とインダクタンスのみの直列回路を考えます。
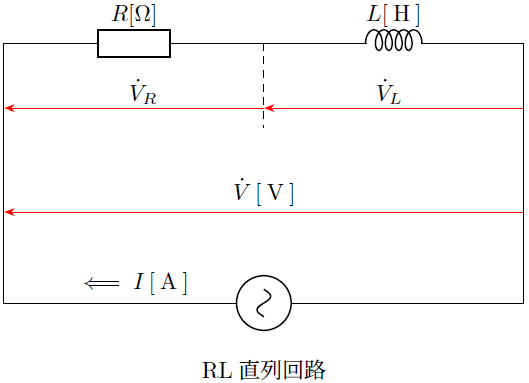
このインダクタンスと抵抗のみの直列回路において角周波数を![]() 、電圧を
、電圧を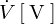 として交流電圧を加えた場合、抵抗
として交流電圧を加えた場合、抵抗![]() と
と![]() に同値の電流
に同値の電流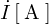 が流れ、またベクトル図で考えると
が流れ、またベクトル図で考えると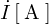 の位相は
の位相は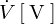 より角度
より角度![]() の分だけの遅れが生じることになります。
の分だけの遅れが生じることになります。
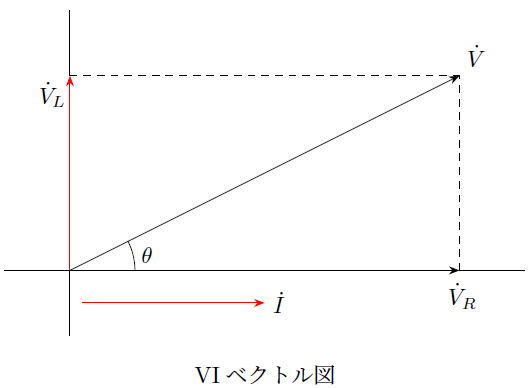
ここで電流![]() は、抵抗
は、抵抗![]() の端子電圧を
の端子電圧を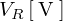 、インダクタンス
、インダクタンス![]() の端子電圧の値を
の端子電圧の値を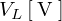 とすれば、それぞれの電圧は以下のように求まることになります。
とすれば、それぞれの電圧は以下のように求まることになります。
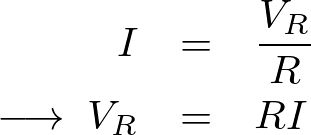
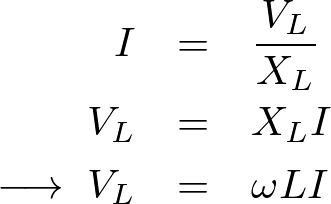
ここで上記のベクトル図に対して、三平方の定理を適用すると次のような関係式が求まることになります。
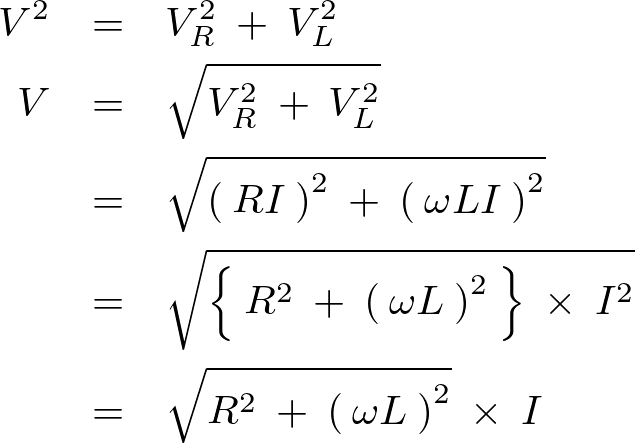
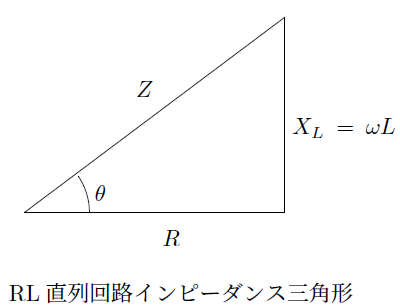
先ほどのベクトル図における![]() の値を
の値を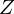 と置いた場合、三平方の定理によって左のような三角形の関係を考えることができます。これをインピーダンス三角形と呼びます。
と置いた場合、三平方の定理によって左のような三角形の関係を考えることができます。これをインピーダンス三角形と呼びます。
全電流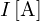 の大きさはオームの法則より以下、
の大きさはオームの法則より以下、
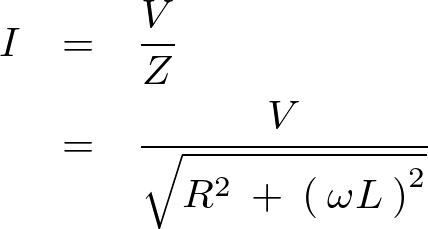
これによって![]() 直列回路における交流回路の抵抗インピーダンスは次のようになります。
直列回路における交流回路の抵抗インピーダンスは次のようになります。
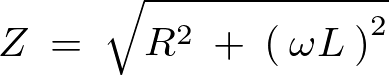
例題1
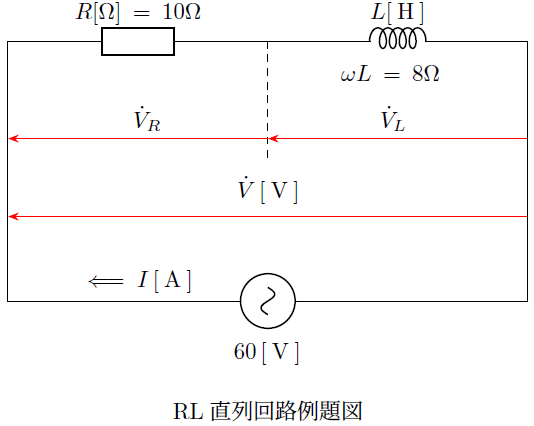
上記のような抵抗が![]() 、リアクタンスが
、リアクタンスが![]() の場合のインピーダンスの値と電流を求めます。
の場合のインピーダンスの値と電流を求めます。
まずインピーダンスの値に関して、
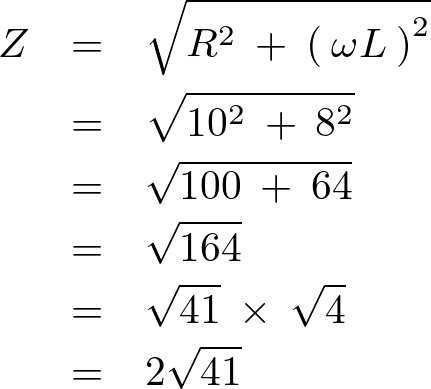
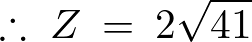
これによって電流は、

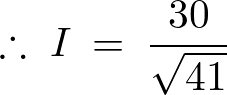
RC直列回路
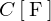 次のような抵抗
次のような抵抗![]() と静電容量
と静電容量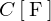 のみのRC直列回路を考えます。
のみのRC直列回路を考えます。
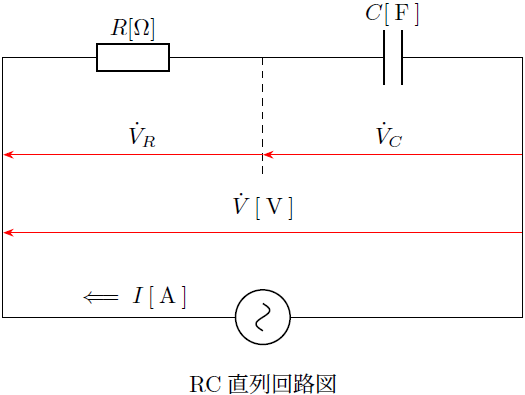
このとき![]() と
と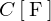 には同一の電流が流れ
には同一の電流が流れ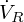 と
と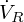 の位相は同位相になり、静電容量は端子電圧の大きさを
の位相は同位相になり、静電容量は端子電圧の大きさを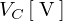 とすると、
とすると、
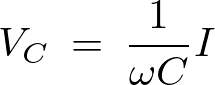
このとき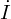 の位相は
の位相は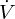 の位相より角度
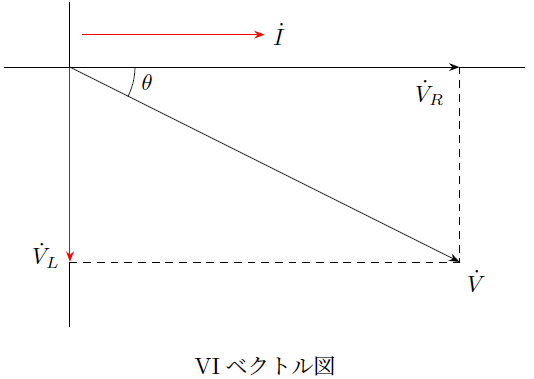
の位相より角度![]() の分だけ反時計回りに進むので以下のようなベクトル図の関係になります。
の分だけ反時計回りに進むので以下のようなベクトル図の関係になります。
例題2
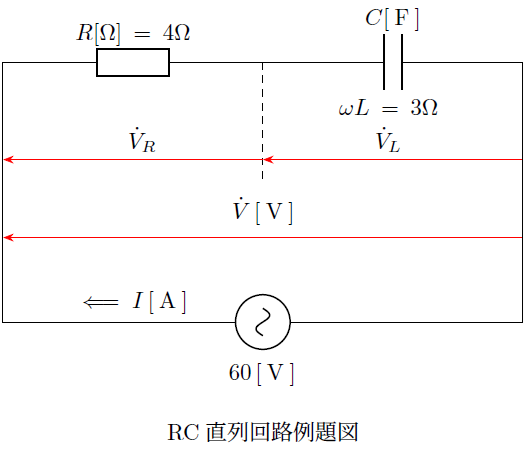
上記のような抵抗![]() と
と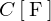 のみの回路において、抵抗は
のみの回路において、抵抗は![]() 、静電容量が
、静電容量が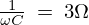 の場合のインピーダンスの値と電流の値は以下のように求められます。
の場合のインピーダンスの値と電流の値は以下のように求められます。
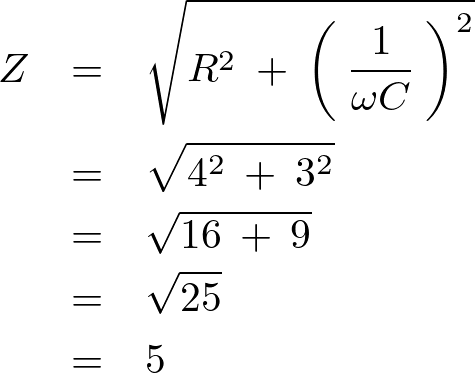
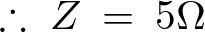
これによって流れる電流の値は以下のように求まります。
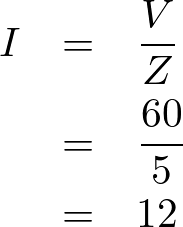
-
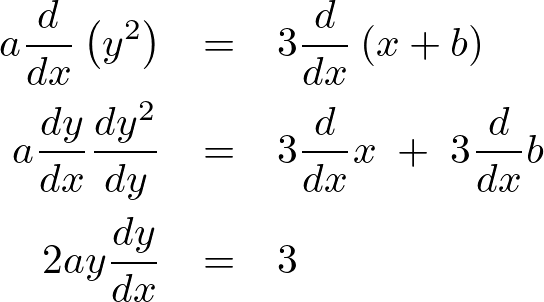
微分方程式いろいろTOPページLaTeXコード
続きを読む
-
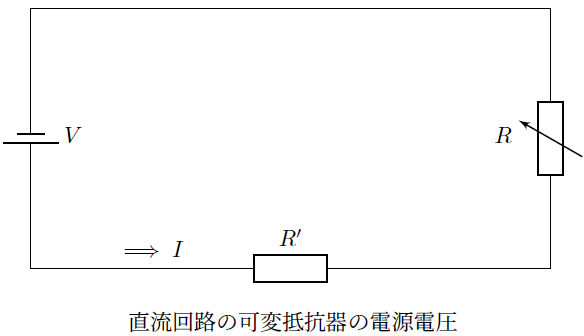
可変抵抗器の直列回路
続きを読む
-
Cisco Packet Tracer
続きを読む
-
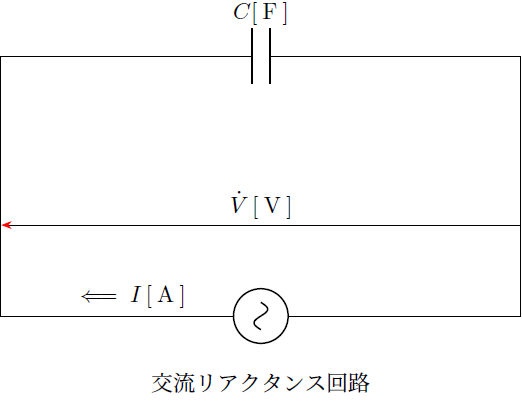
交流回路
続きを読む
-
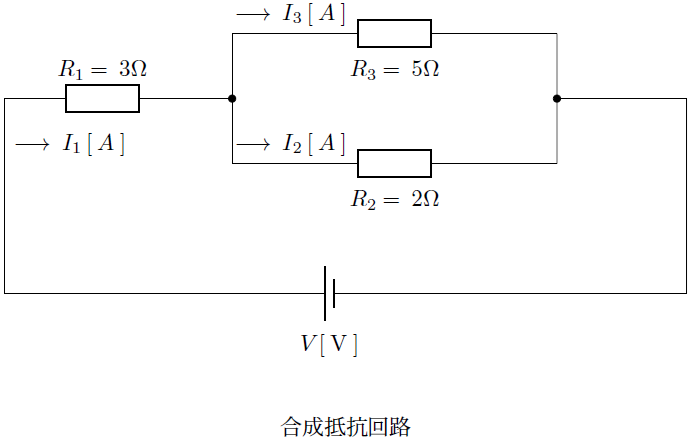
直流回路の合成抵抗
続きを読む
-
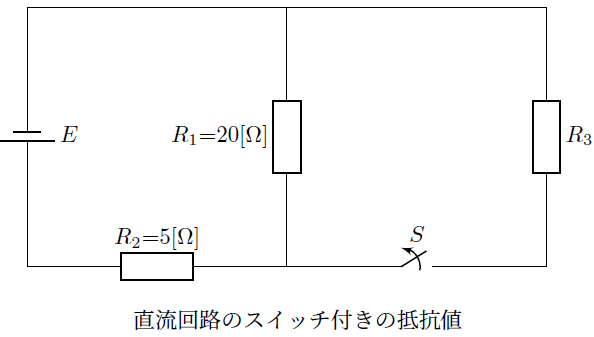
スイッチ付き回路素子の抵抗値
続きを読む
