Visual Studio
Visual Studioインストール
Visual Studio Community 2022 のインストール
AzureといったクラウドサービスをサポートするためのVisual Studio Community 2022をインストールした際の覚書になります。
https://visualstudio.microsoft.com/ja/vs/community
かなりの機能を持ち合わせた統合開発環境になりますが個人で使う分には全くの無料のようです。遠慮なくダウンロードしましょう。
ちなみに実装するまでかなり時間がかかるので時間に余裕がある休日などで行うのがいいかと思います。
参考:https://learn.microsoft.com/ja-jp/visualstudio/install/install-visual-studio?view=vs-2022
ダウンロードしたらダブルクリックでインストールを実行します。
左のキャプチャ画像のように出てくるので続行をクリックしてデフォルトで進めていきます。
ワークロードの選択
自分の目的に合わせたものを選んでインストールをクリックします。
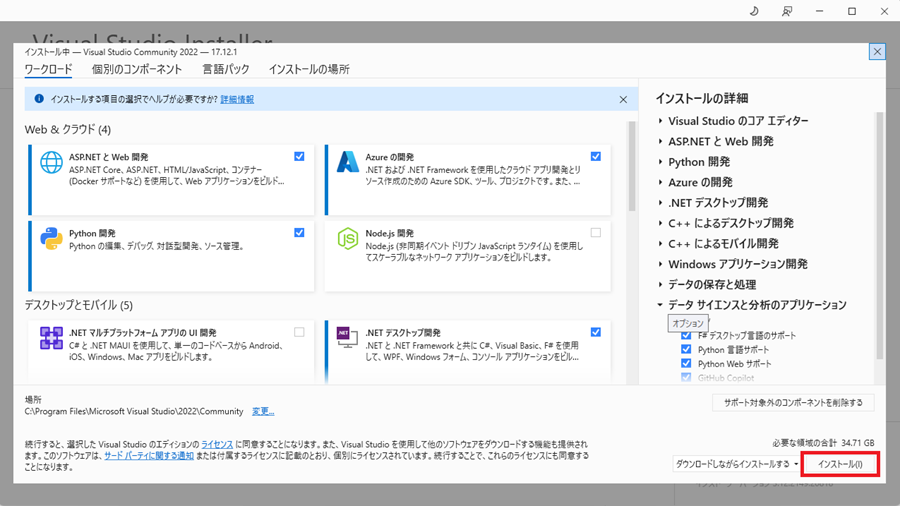
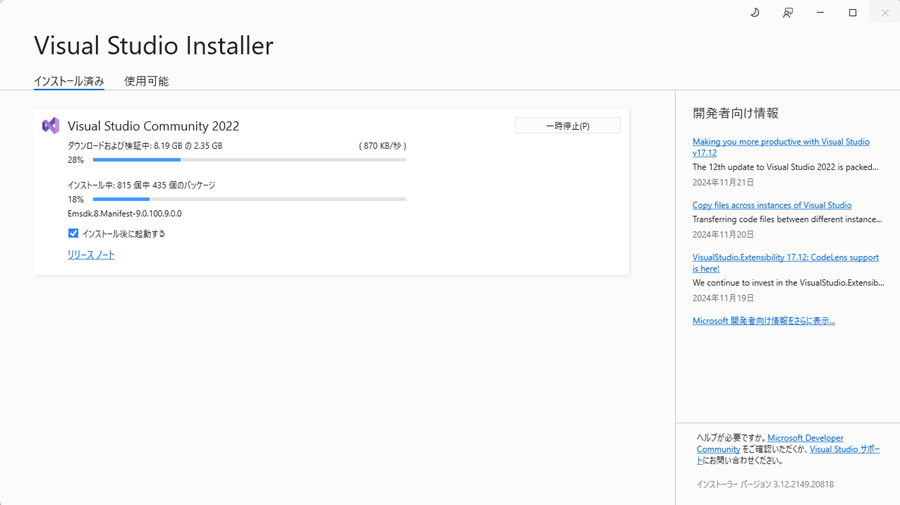
環境によっては以下のようになるまでにかなりの時間がかかる場合があります。私の場合は昼ごろに上記始まってから以下のようなまでなったのは夜になってからでした。
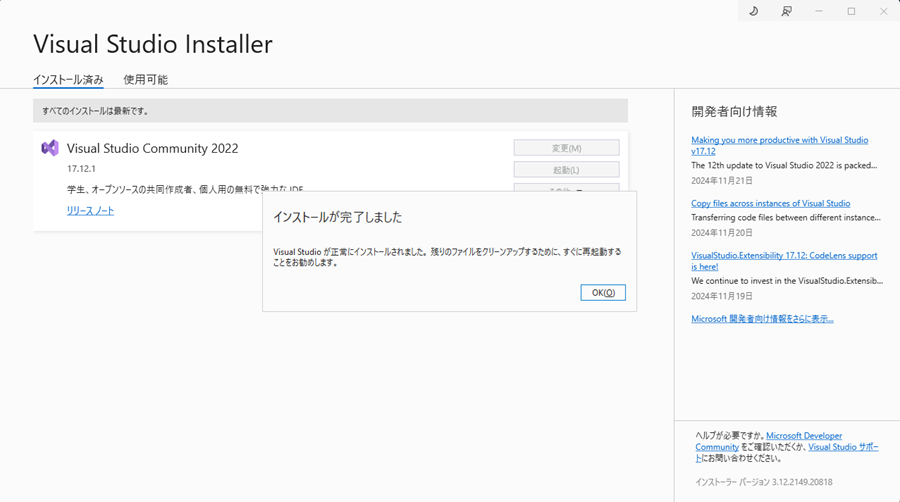
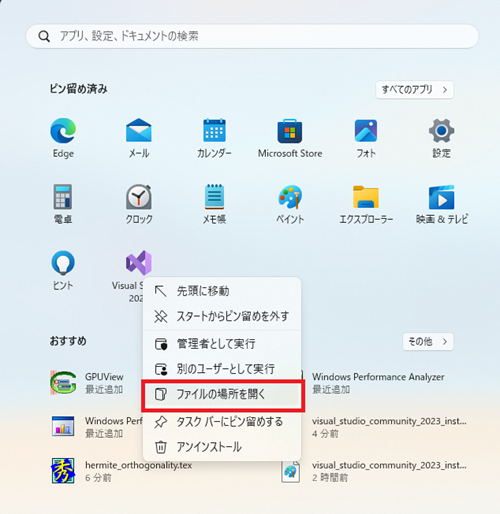
デスクトップに起動アイコンを作成するためにウインドウズボタンを押してVisual Studio 2022のアイコンを右クリックして「ファイルの場所を開く」をクリックします。
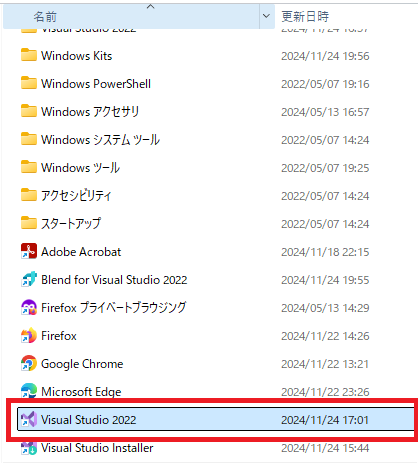
ファイルのある場所に移動したら左キャプチャ画像の赤枠の中のVisual Studio 2022を右クリックします。
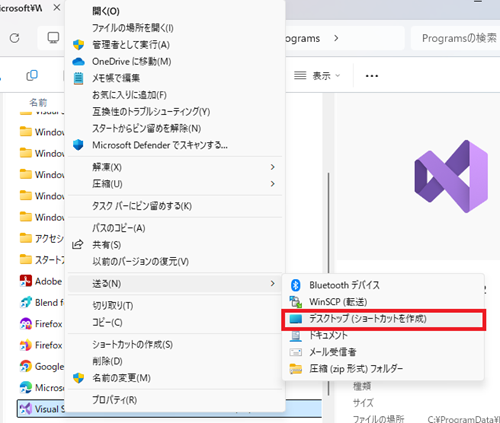
右クリックで「送る」→「デスクトップ(ショートカットを作成)」をクリックでアイコンをデスクトップ上に表示させます。
コードの実行(Pythonの場合)
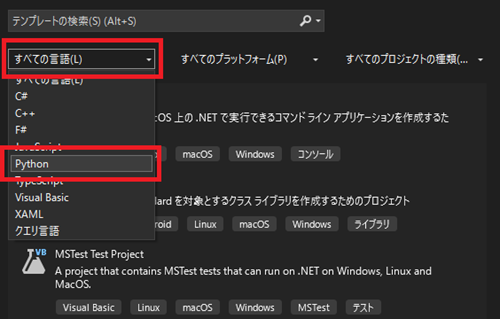
新しいプロジェクトの作成をクリックしたら左のキャプチャ画像の選択画面が出てくるので3つあるセレクトボタンの一番左から「Python」を選択。
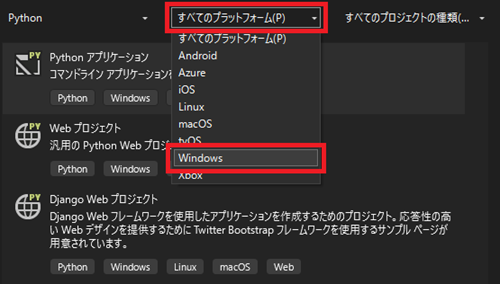
3つあるセレクトから今度は真ん中の「すべてのプラットフォーム」から「Windows」を選択します。
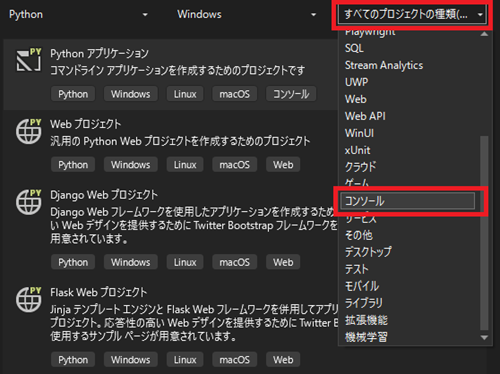
すべてのプロジェクトの種類より、「コンソール」を選択します。
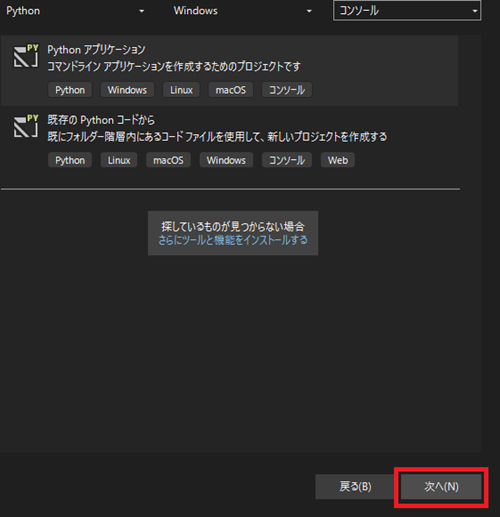
選択が終わったら「次へ」をクリックします。
ファイル名は好きなように。以下の場合作業フォルダをC:pythonwork~下に作成し、下の「ソリューションとプロジェクトを同じディレクトリ~」にチェックを入れます。入れない場合はパスを通すか、コンソールでディレクトリを移動するようにします。
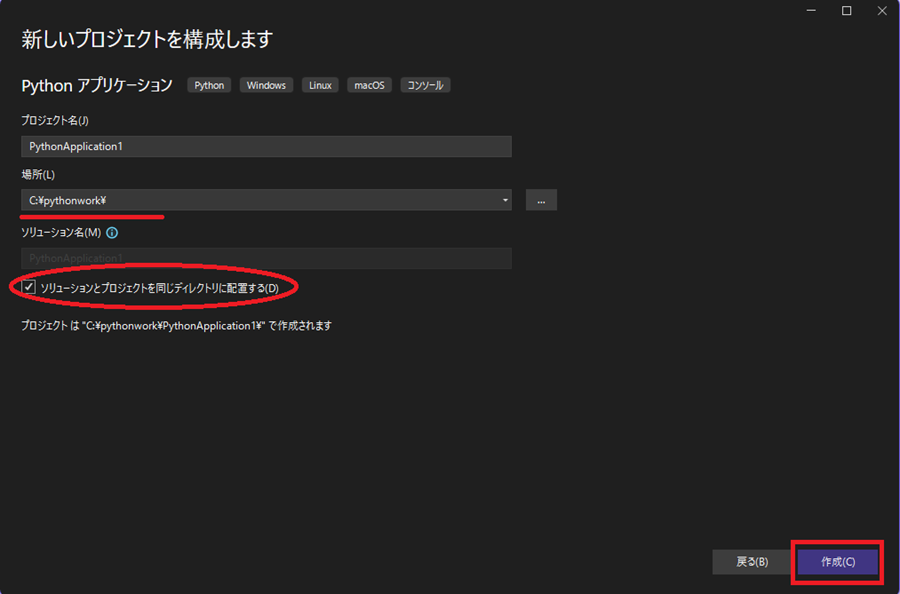
簡単なコードを書いてコンパイルしようとしたところ以下のようなメッセージが出てきます。
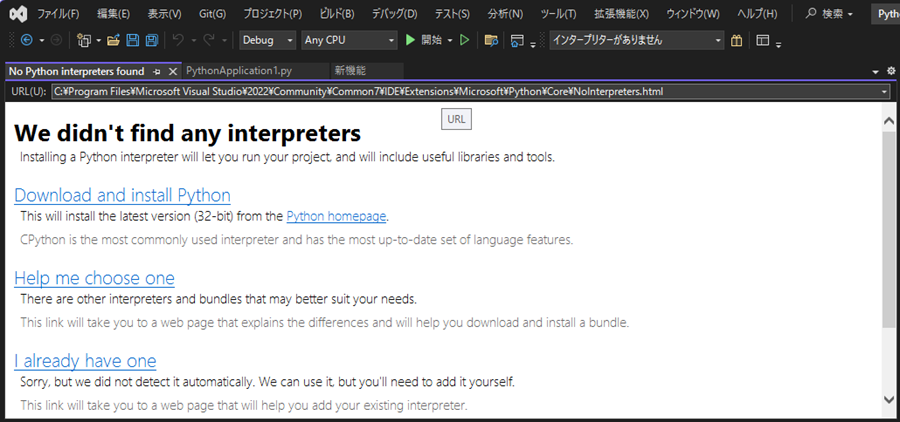
インタプリタ―がありませんと出ており、新端末でのPythonのインストールをしていなかったのでパスが通っていなかったためpython.exeを認識できず上記のようになったようです。
Pythonの実装
Pythonの最新のexeファイルをダウンロードします。
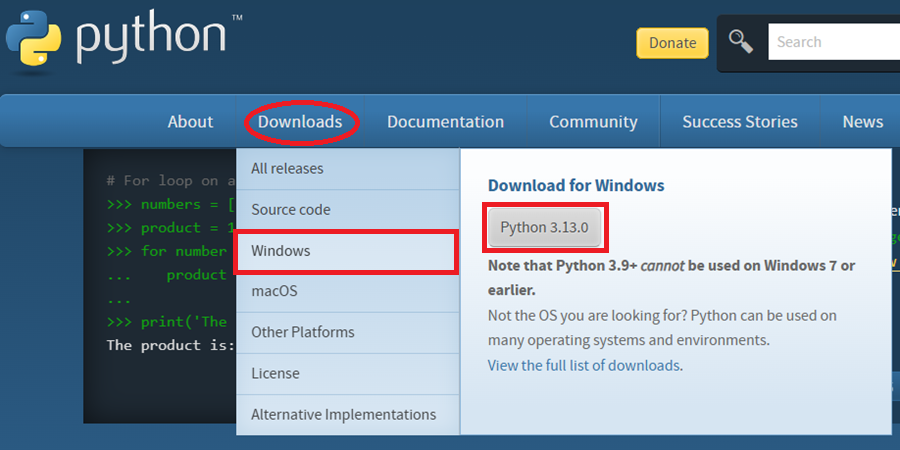
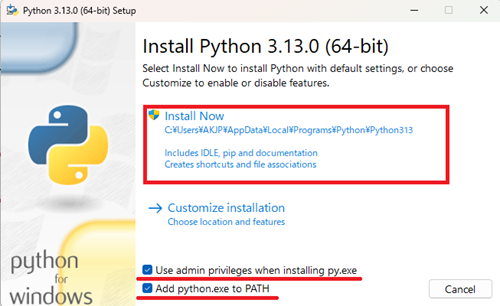
ダウンロードが終わったらexeファイルを展開してインストールをし、左キャプチャ画像になったら下側のAdd python.exe to PATHにチェックを入れてから四角赤囲みの「Install Now」をクリックしてインストールを実行します。
環境を追加をクリックします。
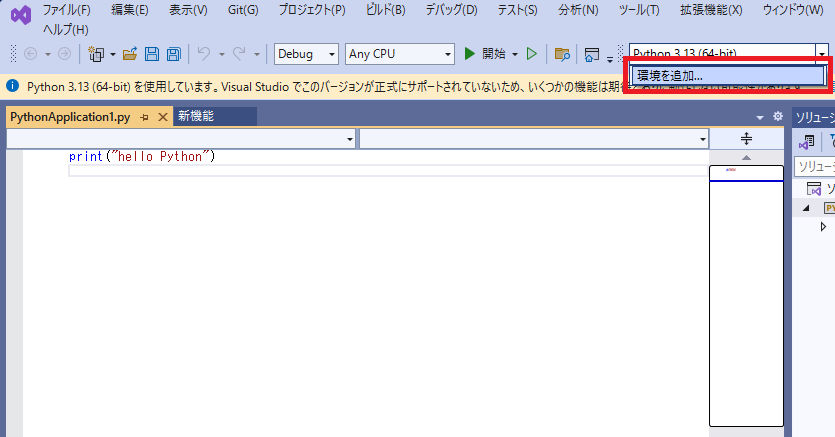
以下のようにパスが通っていることが確認できます。
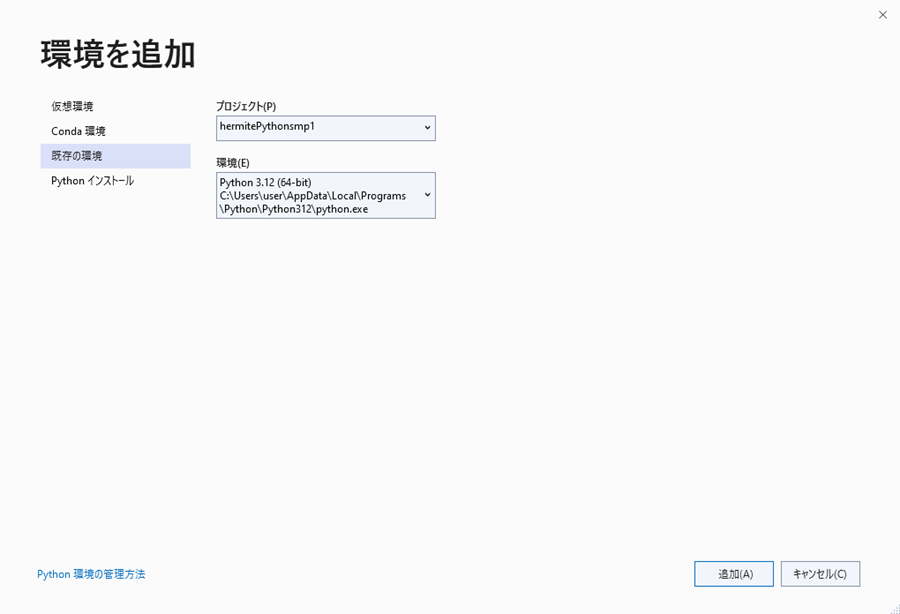
その他ライブラリのインストールなど
コマンドプロンプトを開いてpipの確認をすると次のようになっていることがわかります。
C:\Users\user>python -V Python 3.12.7 C:\Users\user>pip list Package Version ------- ------- numpy 1.26.4 pip 24.3.1 C:\Users\user>
グラフ描画のためのmatplotlibなどが入っていないのでまず最初に以下のコマンドでpipの更新とsetuptoolsの更新を行います。
python -m pip install --upgrade pip setuptoolswidth
再度pipを行うと次のように表示されるようになります。
C:\Users\user>pip list Package Version --------------- ----------- contourpy 1.3.1 cycler 0.12.1 fonttools 4.55.0 kiwisolver 1.4.7 matplotlib 3.9.2 numpy 2.1.3 packaging 24.2 pillow 11.0.0 pip 24.3.1 pyparsing 3.2.0 python-dateutil 2.9.0.post0 setuptools 75.6.0 six 1.16.0
動作確認
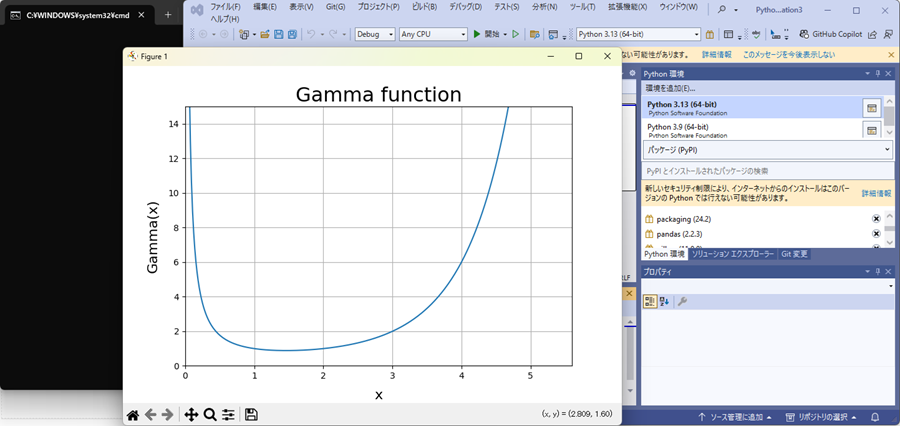
以下のコードはガンマ関数と呼ばれるものを描画するためのコードになります。
from math import gamma
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.01, 5.6, 350)
gamma_func = np.frompyfunc(gamma, 1, 1)
y = gamma_func(x)
fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111)
ax.set_title("Gamma function", size = 23)
ax.grid()
ax.set_xlim(0, 5.6)
ax.set_ylim(0, 15)
ax.set_xlabel("x", size = 16, labelpad = 10)
ax.set_ylabel("Gamma(x)", size = 16, labelpad = 10)
ax.plot(x, y)
plt.show()
上部メニューの「デバック」→「デバックなしで開始」とやると以下のように画像が出力されます。
パッケージの追加方法
上記のやり方で例えばnumpyやmatplotlibがないと出て出力及びデータの処理ができない、または新たに別のライブラリをいれたいときなどはコンソール画面上で直接取り込みしたほうが早いです。
姉妹サイト「微分方程式いろいろ」というWebサイトで現在作成中になっている数学コンテンツでエルミート多項式というのがあります。それを描画するためのコードは以下のようになります。
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import eval_hermite
x = np.arange(6)
h = eval_hermite(3, x)
print(h)
x = np.linspace(-4, 4, 129)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)
ax.set_title("Hermite functions", size = 15)
ax.grid()
ax.set_xlim(-4, 4)
ax.set_ylim(-30,30)
ax.set_xlabel("x", size = 14, labelpad = 8)
ax.set_ylabel("Hn(x)", size = 14, labelpad = 8)
c = ["red", "blue", "green", "darkorange", "aliceblue", "orange"]
for i in range(5):
ax.plot(x, eval_hermite(i, x),
label = "n = {}".format(i), color = c[i-1])
ax.legend()
plt.show()
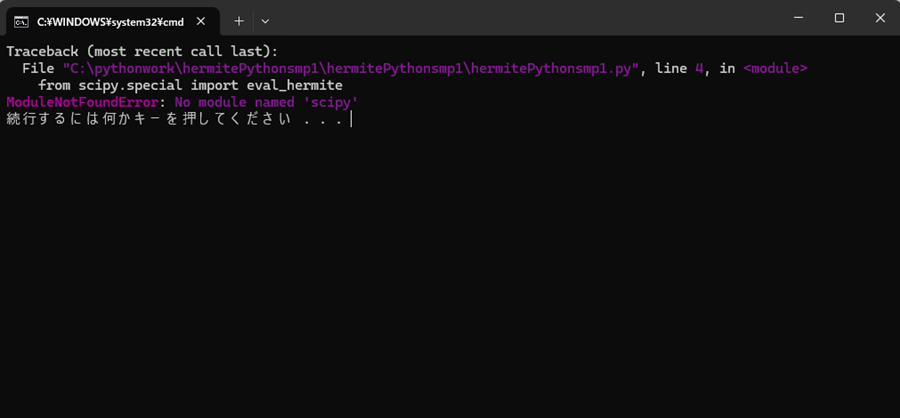
これをそのまま走らせると次のようにエラーが出て描画ができません。
Traceback (most recent call last):
File "C:\pythonwork\hermitePythonsmp1\hermitePythonsmp1\hermitePythonsmp1.py", line 4, in <module>
from scipy.special import eval_hermite
ModuleNotFoundError: No module named 'scipy'
続行するには何かキーを押してください . . .
エラーの内容としてはscipyという名前のモジュールがないと出てきます。こういった場合は次のようにします。
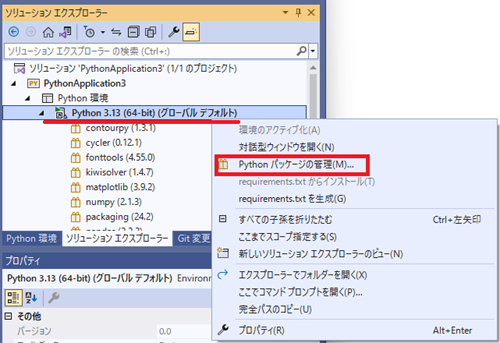
ソリューションエクスプローラーのPython環境下にあるPython 3.13(64-bit)~のところを右クリックして「Pythonパッケージの管理(M)」となっているところをクリックします。
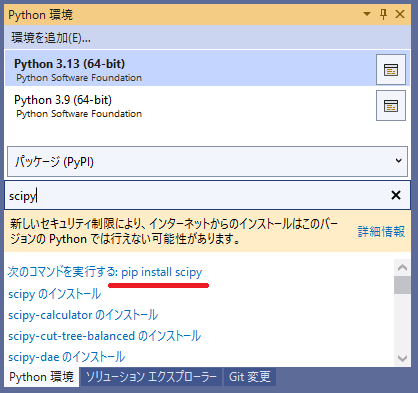
そうすると左のキャプチャ画像のようなPython環境の追加のタブが出てくるので、ここで検索箇所(赤四角囲み部分)にscipyと入力します。
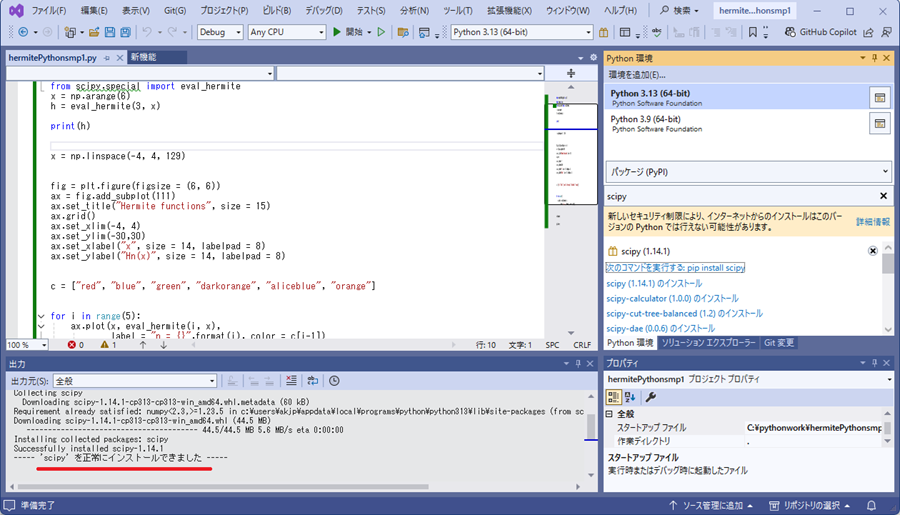
赤線の部分のように次のコマンドを実行する:pip install scipyと出てくるのでこれをクリックします。
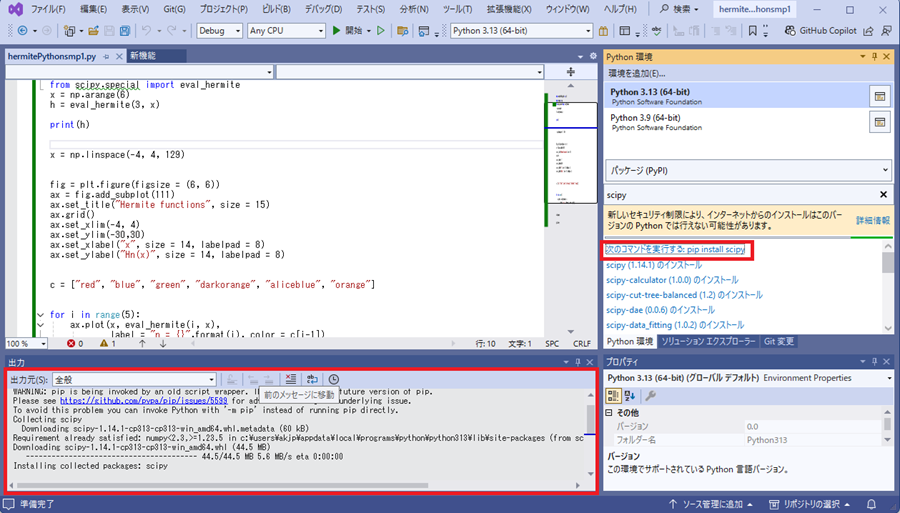
正常にインストールが終わるとターミナル画面上に以下のように表示されます。
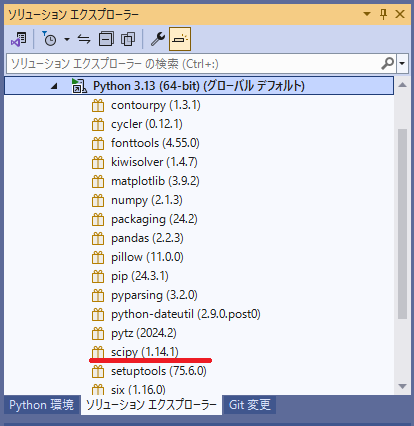
ソリューションエクスプローラーを開くと、キャプチャ画像のようにscipyが追加されていることがわかります。
最後にpip listでも確認してみます。
PS C:\Users\user> pip list Package Version --------------- ----------- contourpy 1.3.1 cycler 0.12.1 fonttools 4.55.0 kiwisolver 1.4.7 matplotlib 3.9.2 numpy 2.1.3 packaging 24.2 pandas 2.2.3 pillow 11.0.0 pip 24.3.1 pyparsing 3.2.0 python-dateutil 2.9.0.post0 pytz 2024.2 scipy 1.14.1 setuptools 75.6.0 six 1.16.0 tzdata 2024.2 PS C:\Users\user>
pip listでもscipyが追加されていることがわかります。
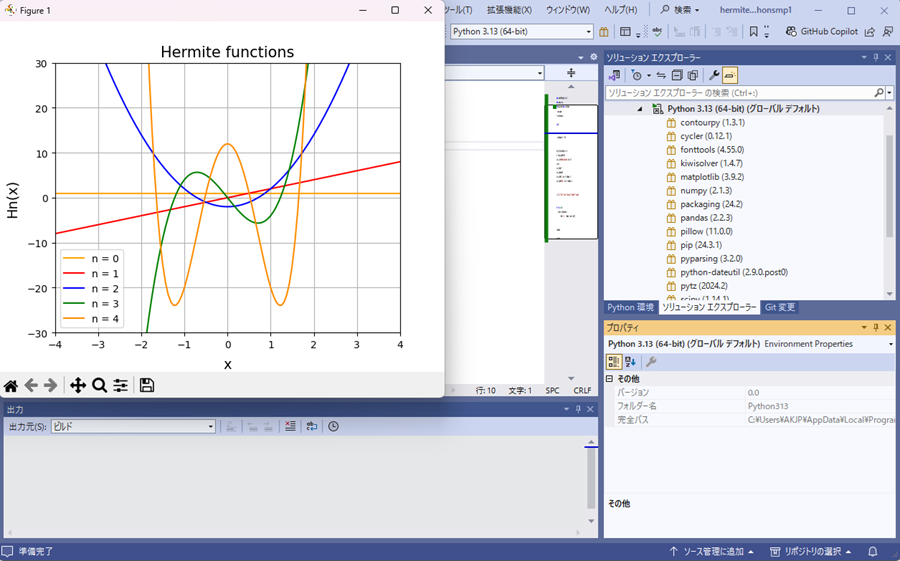
これでコンパイルすると先ほどはエラーが出て画像の出力ができなかったものが、次のようなエルミート多項式の描画が出力されるようになります。
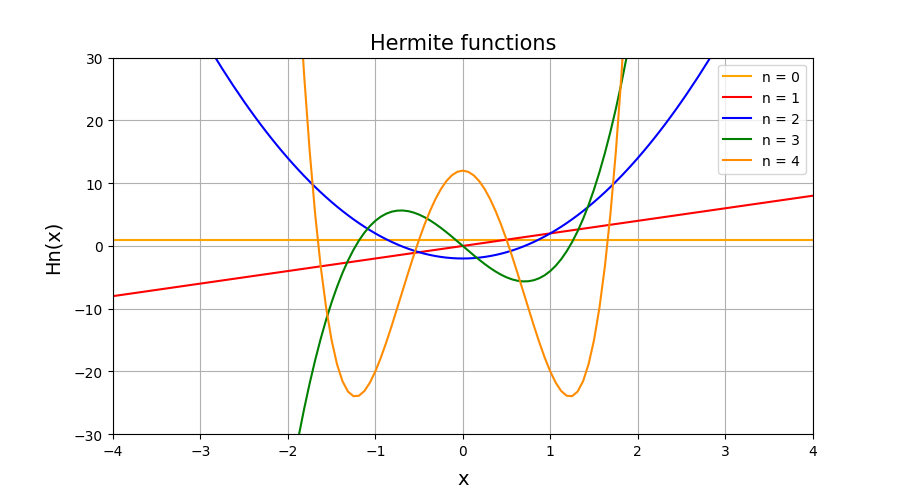
なおこのエルミート多項式のPyhonコードに関しては以下のサイト様の内容を参考に作成しております。
参考サイト:Python 数値計算ノート 様
エルミート多項式の定義・正規化・グラフ | Python 数値計算ノート
-
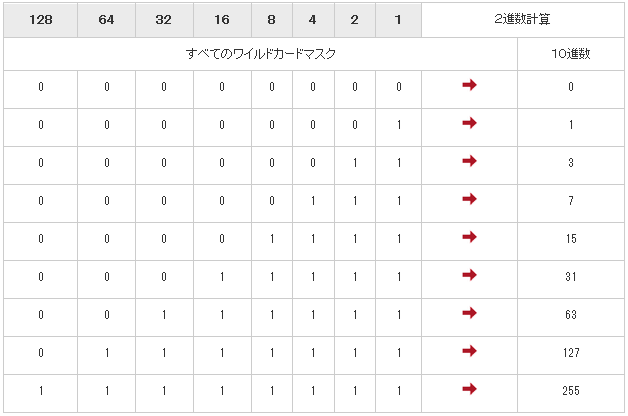
ワイルドカードマスク
続きを読む
-

サブネットマスク
続きを読む
-
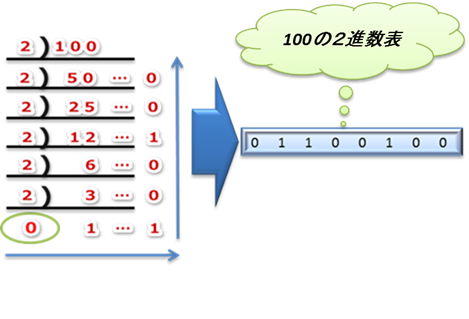
IPアドレス
続きを読む
-

ルータ1台での基本操作
続きを読む
-
テラタームの設定
続きを読む
-
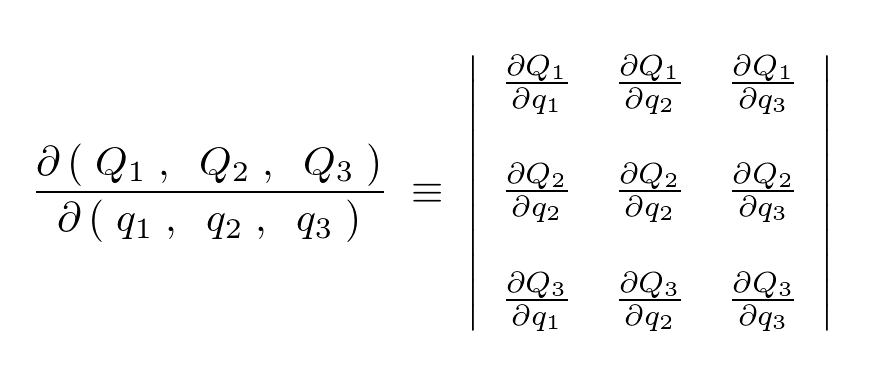
dvの計算法-ヤコビアンを使うやり方
続きを読む
コリオリの力とは
フランスの科学者で軍属でもあったガスパール・ギュスターブ・コリオリ
初歩的な力学の分野において慣性系に関する話の中にコリオリの力というものがあります。
この“コリオリ”とは人の名前であり地球が回転することによっておこる見かけの運動力を、回転座標上で移動したときの移動方向と垂直な方向に受ける慣性力の一種を数式で表現したものになります。
一般的にこのコリオリという人物は科学者という記述が多いのですが実は軍人でもあったことはあまり知られていないようです。
北半球において大砲を撃ったとき、その弾道が標的よりもわずかに右にずれることを数式によって説明した人物ということで自衛隊でも多少知られた存在らしく、話の小ネタとして話題になることもありました(おそらく重迫撃砲(ヘヴィモータ)などではコリオリの力による弾道補正が必要になるためだと思います)。
回転座標で運動する物体
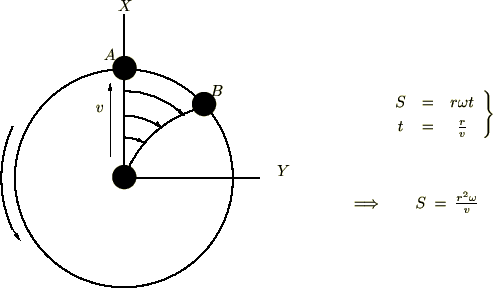
円運動の角度を![]() 、周囲に沿った距離を
、周囲に沿った距離を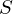 、ボールの速度を
、ボールの速度を![]() 、慣性力を
、慣性力を![]() とおくと、
とおくと、
上の図は、矢印の通りに回転させた円盤を真上からみたものであり、中心から外側へ投げた球があたかも右のほうへずれたように見えるその様子を表したものです。中心部分にいる人物は図の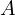 の方向へ投げたつもりが
の方向へ投げたつもりが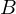 のほうへまるで曲がって投げたように見えてしまいます。
のほうへまるで曲がって投げたように見えてしまいます。
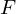 はは動径方向に垂直な方向に働く慣性力とし、一定加速度での移動距離は
はは動径方向に垂直な方向に働く慣性力とし、一定加速度での移動距離は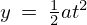 の形で表せるので、
の形で表せるので、
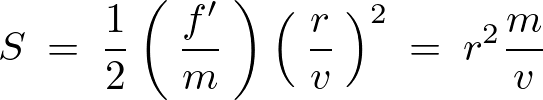
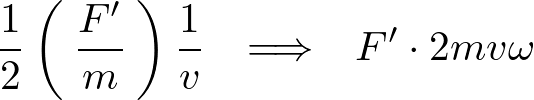
この力をコリオリの力と呼び、回転座標系で運動する物体に加わる慣性力のことを言います。
この力を実際に数式を使って具体的に表現してみましょう。

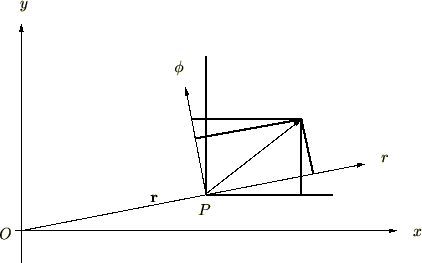
左の座標系が3次元での回転、右の座標系の図が2次元での回転を表したものになります。
これより回転座標系において時間変化した角度を![]() とすれば以下のように表せます。
とすれば以下のように表せます。
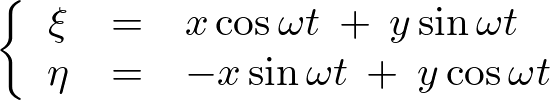
または、
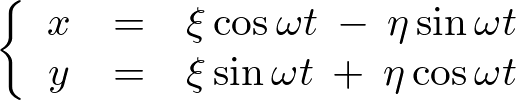
これを時間で微分します。
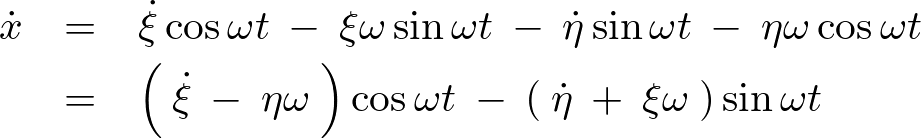
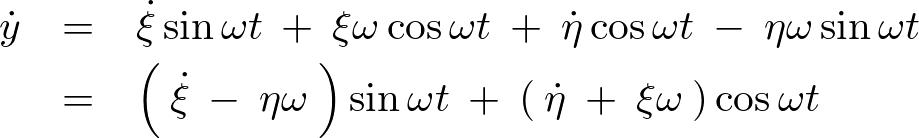
上記式を再度時間微分します。
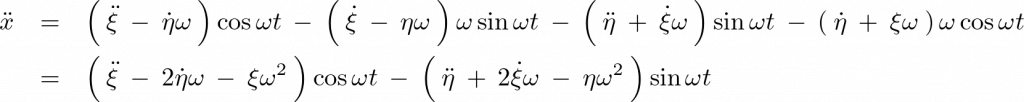
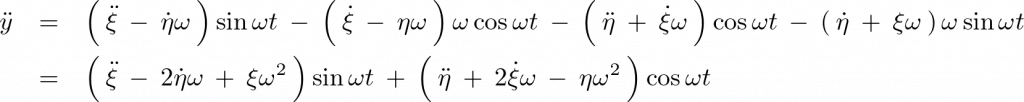
力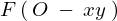 と
と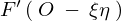 の間の関係は次式で表されます。
の間の関係は次式で表されます。
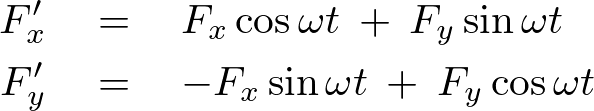
さらに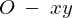 系(慣性系)では次のような運動方程式、
系(慣性系)では次のような運動方程式、
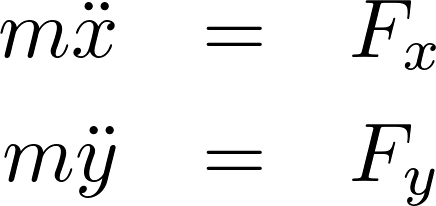
が成り立つので上の式の結果を用いて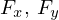 を表せば、
を表せば、
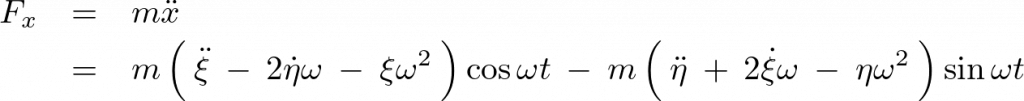
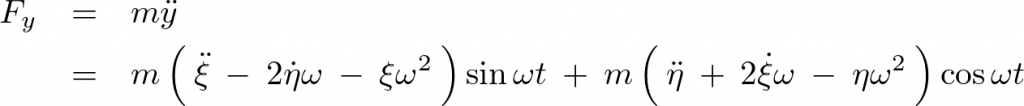
これらを代入し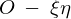 系の座標について整理すれば、
系の座標について整理すれば、
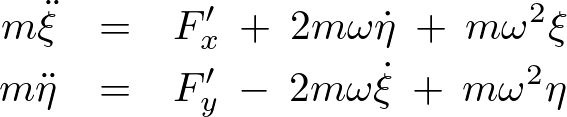
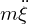 は回転系座標から見た加速度運動で、運動の原因となる力として
は回転系座標から見た加速度運動で、運動の原因となる力として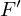 のほかに2つの力が加わった形であり、右辺第2項、第3項は見かけの力(慣性力)を示しています。
のほかに2つの力が加わった形であり、右辺第2項、第3項は見かけの力(慣性力)を示しています。
右辺のそれぞれの意味は、
| 右辺第2項(コリオリの成分) | 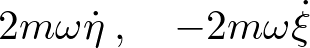 |
| 右辺第3項(遠心力の成分) | 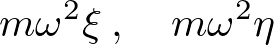 |
を示しています。
回転座標系をまとめてみると次のようになります。
慣性系に対して運動する座標系
| 1. | 等速度運動する座標系は慣性系となる(ガリレイ変換) |
| 2. | 加速度運動する座標系は非慣性系(見かけの力=慣性力)を考える
|
| 3. | 回転運動をする座標系は2種類の見かけの力を考える
|
これらを踏まえて今度は長距離射撃におけるコリオリ弾道軌道計算を考えていきましょう。
次回に続きます。
