定係数2階同次微分方程式
定型数2階同次微分方程式とは
2階微分作用素
オペレータ作用素が2階(2階微分)が入っている以下のような微分方程式を考えます。
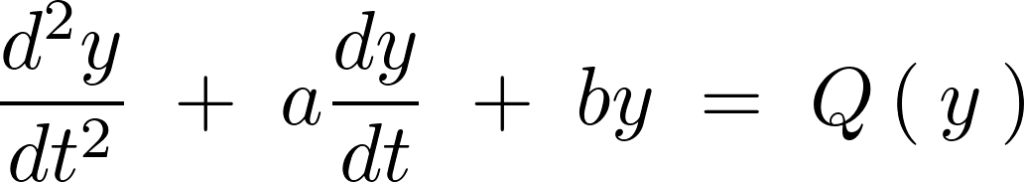
これを定型数2階非同次微分方程式と呼びますが、この式の右辺が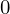 の場合を定型数2階同時微分方程式と呼びます(非同次式の解法はまた別のセクションで取り扱います)。
の場合を定型数2階同時微分方程式と呼びます(非同次式の解法はまた別のセクションで取り扱います)。
なのでこのセクションで扱う微分方程式は以下のようになります。
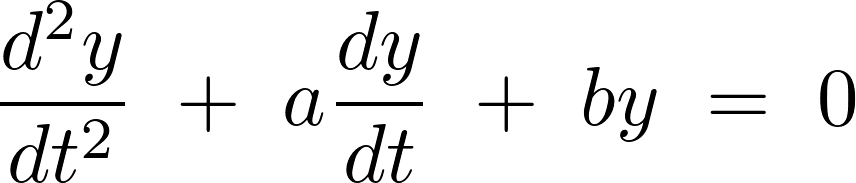
この上記微分方程式の解について考察していきましょう。
今仮に上記微分方程式の解である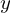 を次のように置きます。
を次のように置きます。
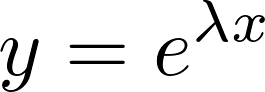
が解であるとします。
これを実際に代入してみると、
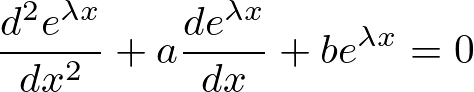
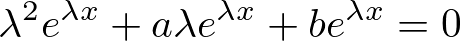
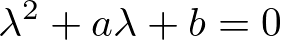
ここで2次方程式とその解の公式は、
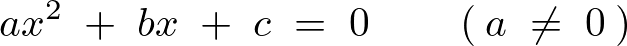
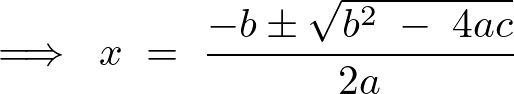
だったのでこれを先ほどの式に当てはめれば、
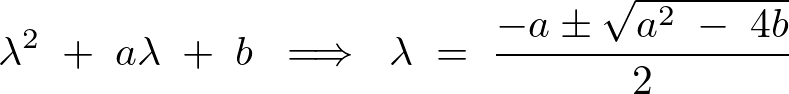
判別法というのを思い出すと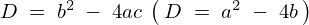 ですが、これによって解の種類が3種類ほどに分別できます。
ですが、これによって解の種類が3種類ほどに分別できます。
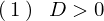 のとき
のとき
解は異なる2つの実数の解 となり、基本解は、
となり、基本解は、

よって一般解は、
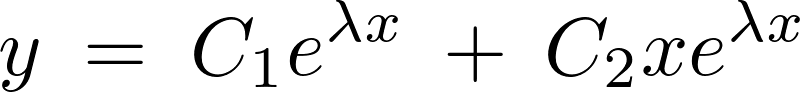
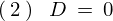 のとき
のとき
解は重解となります。
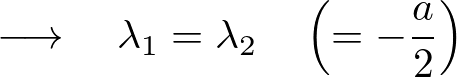
この場合、この特性方程式の根は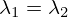 ですが簡単に基本解が同じもの2つということにはなりません。
ですが簡単に基本解が同じもの2つということにはなりません。
![]() 階の微分方程式には
階の微分方程式には![]() 個の任意定数を含む
個の任意定数を含む![]() 個の解が必要です。
個の解が必要です。
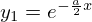 に対して線形独立なもう一つの解を求めます。
に対して線形独立なもう一つの解を求めます。
その2つ目の解を仮に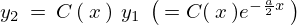 と置きます。
と置きます。
すると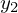 は
は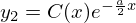 となります。
となります。
これを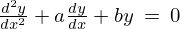 に代入してみると、
に代入してみると、
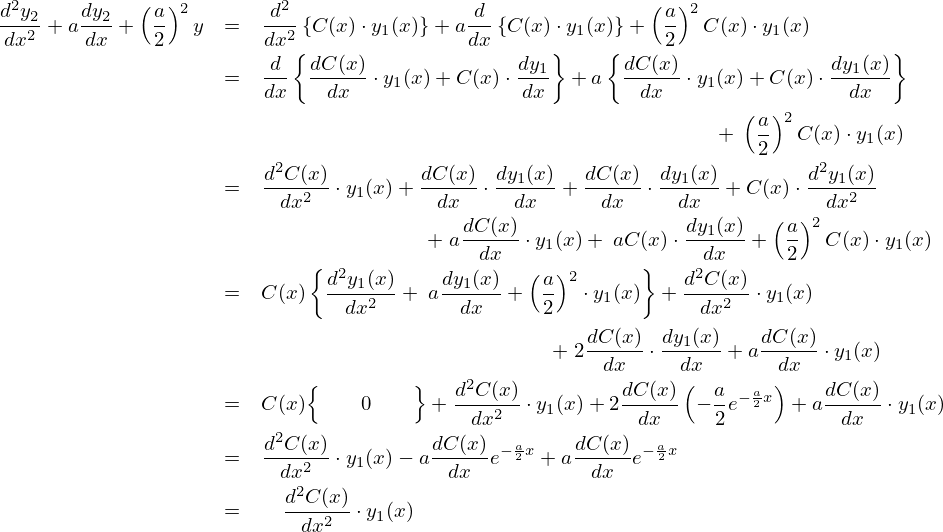
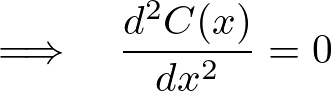
この式を積分していきます。
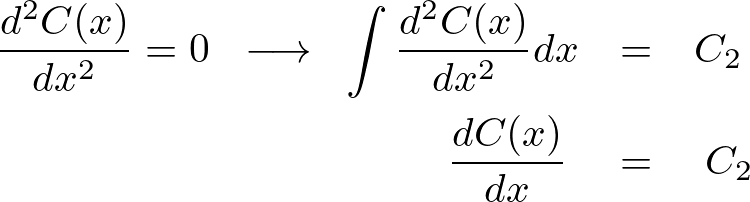
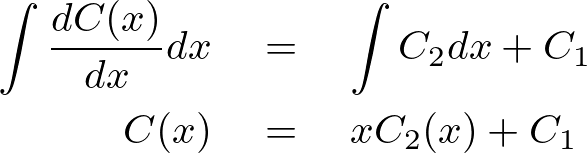
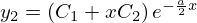 となりますがここでもとめているのは
となりますがここでもとめているのは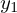 とは違う独立な解を求めることなのでこれを
とは違う独立な解を求めることなのでこれを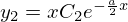 とおきます。
とおきます。
そうすると、
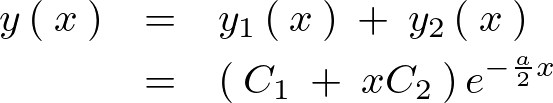
ここで、
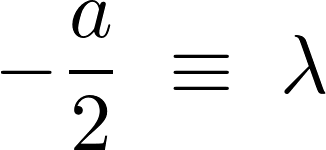
とおけば基本解は、

一般解は次のようになります。
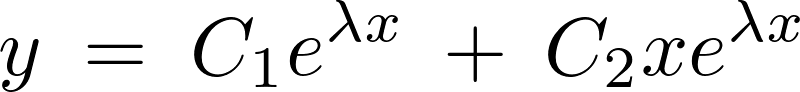
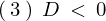 のとき
のとき
このとき解は実数と、それ以外に虚数と呼ばれるものがミックスされた複素共役と呼ばれるものになります。
根は、
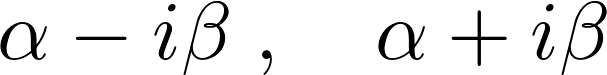
基本解は、
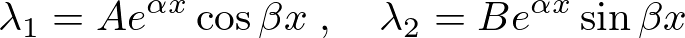
実数が![]() に対応し虚数側が
に対応し虚数側が![]() 、
、![]() といった三角関数のほうに対応しています。
といった三角関数のほうに対応しています。
これの特性方程式は、
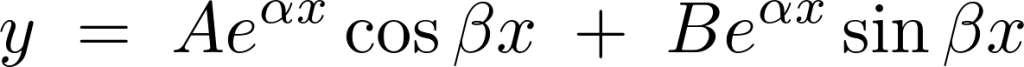
例題
次に示す2階の同次微分方程式を求めてみましょう。
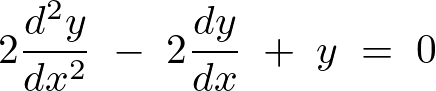
まず特性方程式を作ります。
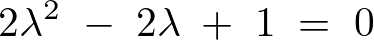
因数分解ができないので解の公式を使って求めていきます。
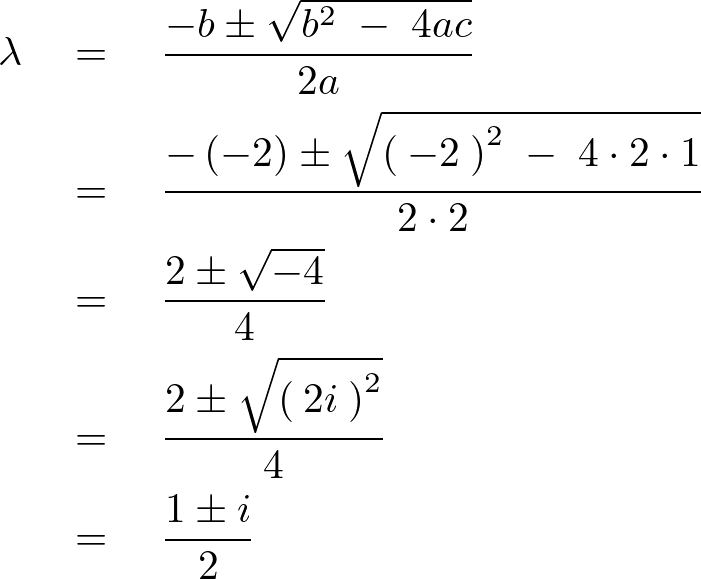
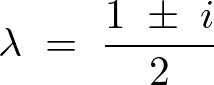
となるので基本解は、
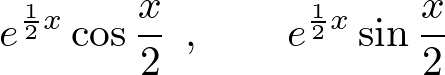
一般解は以下のようになります。
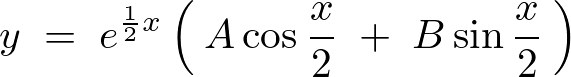
解であることの証明
実際に上記で求まった解が例題の2階同次微分方程式に代入して合っているか確かめてみましょう。
1階微分は、
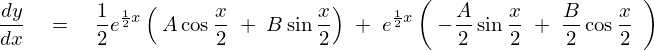
2階微分は、
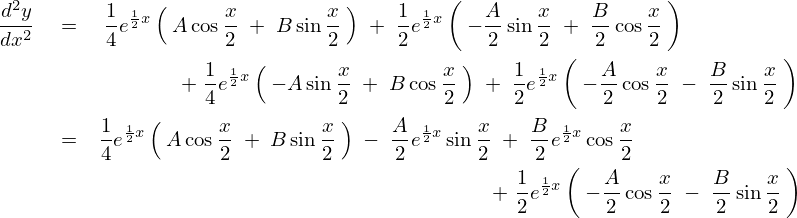
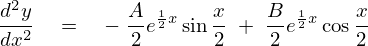
これらを代入していきます。
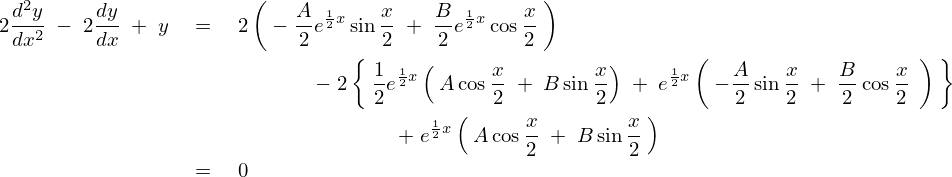
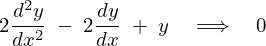
となるので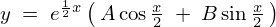 は例題として出された2階同次微分方程式の解であることがわかります。
は例題として出された2階同次微分方程式の解であることがわかります。
1階常微分方程式
作用素が1階のものを1階微分方程式と呼び、変数が2つある場合それぞれを同じ変数同士で分けて、作用素を変化させて計算していきます。
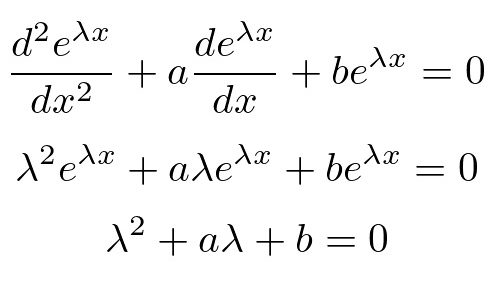
2階同次微分方程式
微分作用素が2階微分入っている微分方程式を考え、この時作用素の入っていない右辺が0の場合を2階同次微分方程式と呼びます。
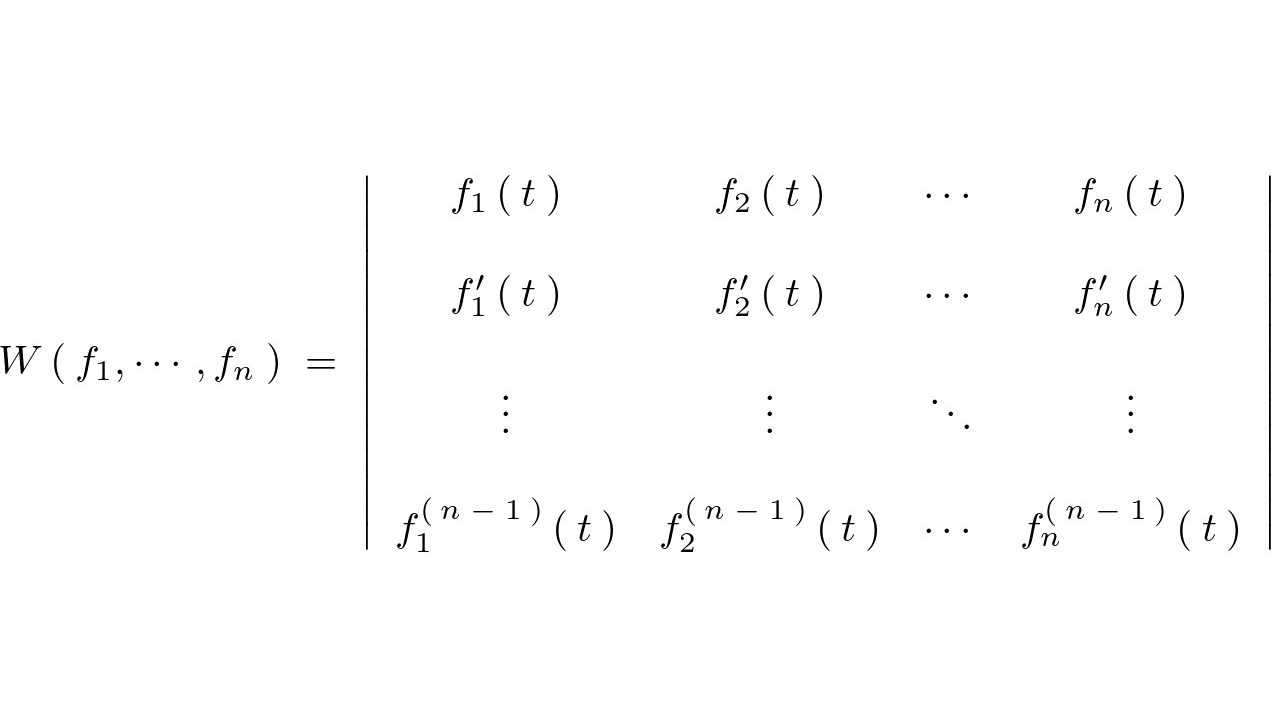
Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。

