エルミート多項式の諸性質
エルミート多項式の変形
今ここでロドリーグの式を思い出すと次のようなものになります。
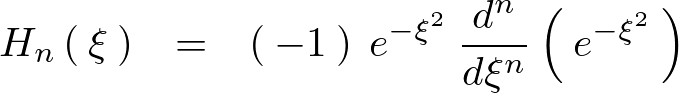
上記式に関して一回微分します。
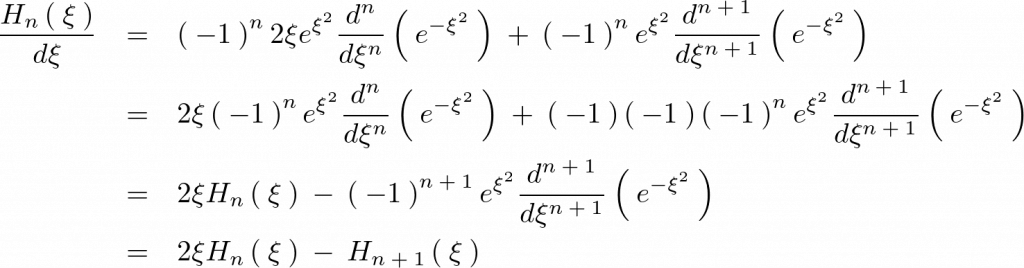
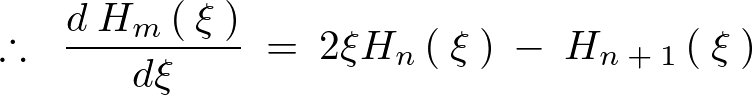
さらに続けて微分します。
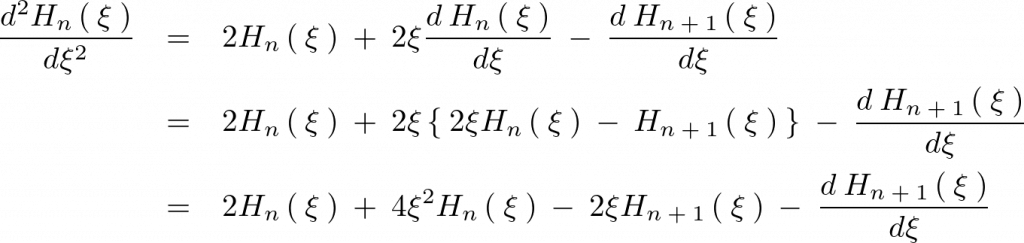
上記式においての右辺第4項目を計算していきます。
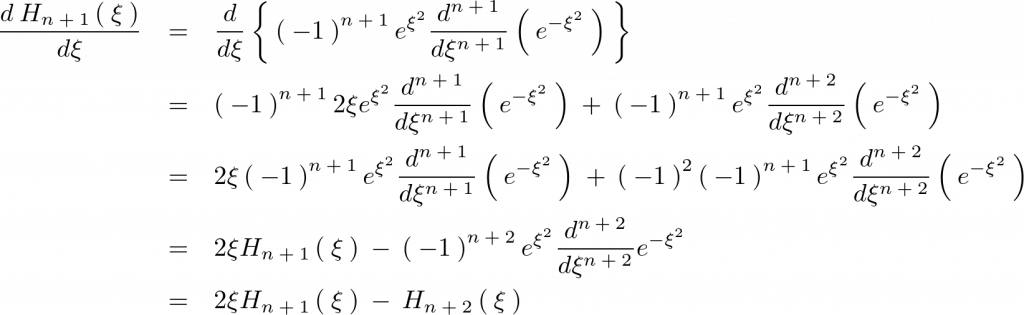
となるので次のような関係式が導かれます。
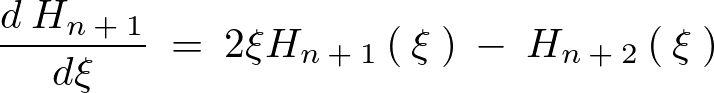
この式を先ほどの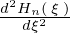 の式に代入して計算していきます。
の式に代入して計算していきます。
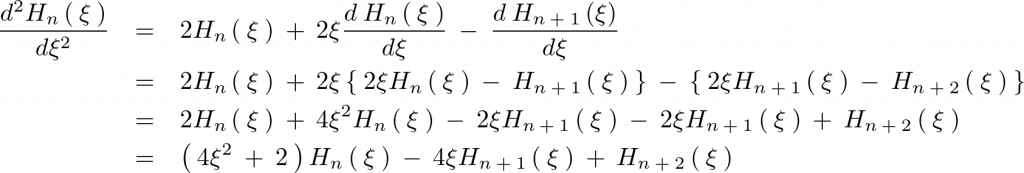
となるので以下の3つの関係式が求まります。
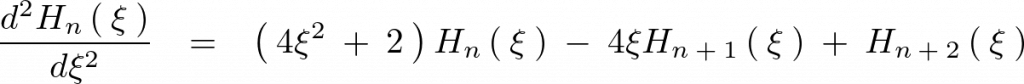
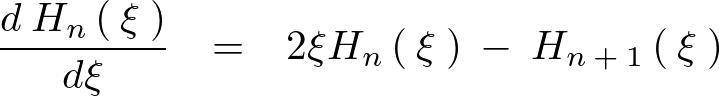
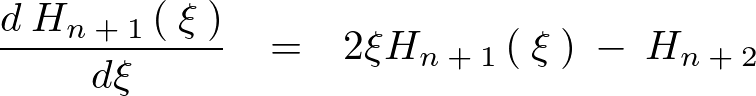
今ここでエルミートの微分方程式を思いだすと、
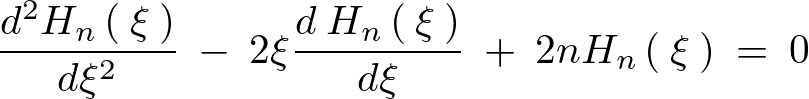
これに代入します。
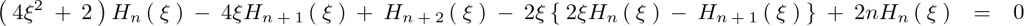
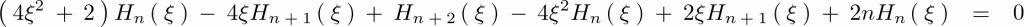
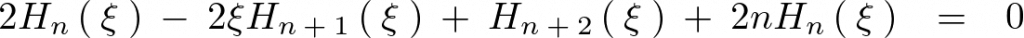
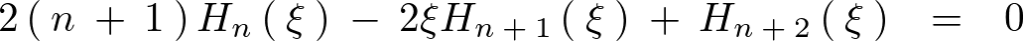
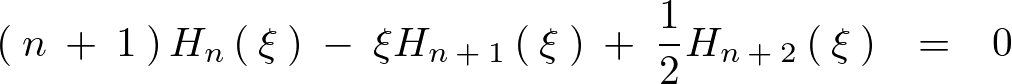
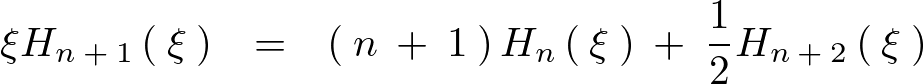
ここで上記式において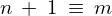 と置きます。
と置きます。
そうして先ほどの式に関して次のようにいったんおきます。
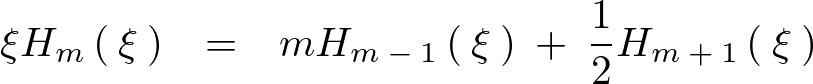
この![]() を
を![]() とおいて、先ほどの次のような式、
とおいて、先ほどの次のような式、
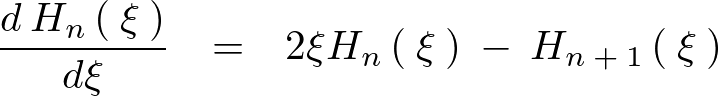
この式の右辺第1項に代入します。
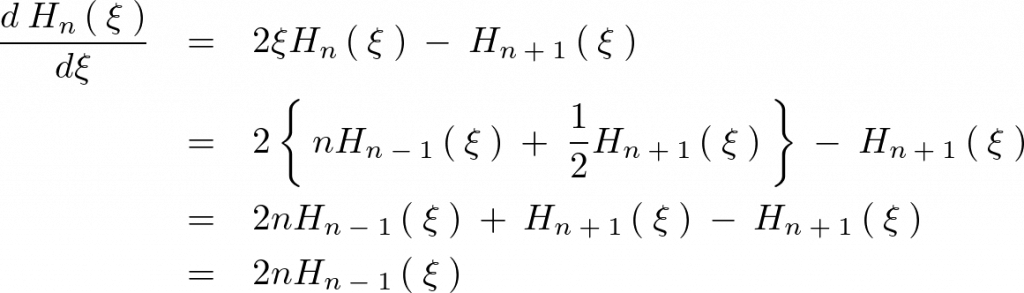
結果的に次のような関係式が求まります。
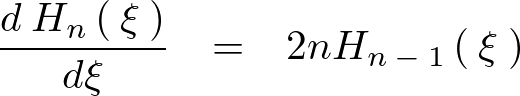
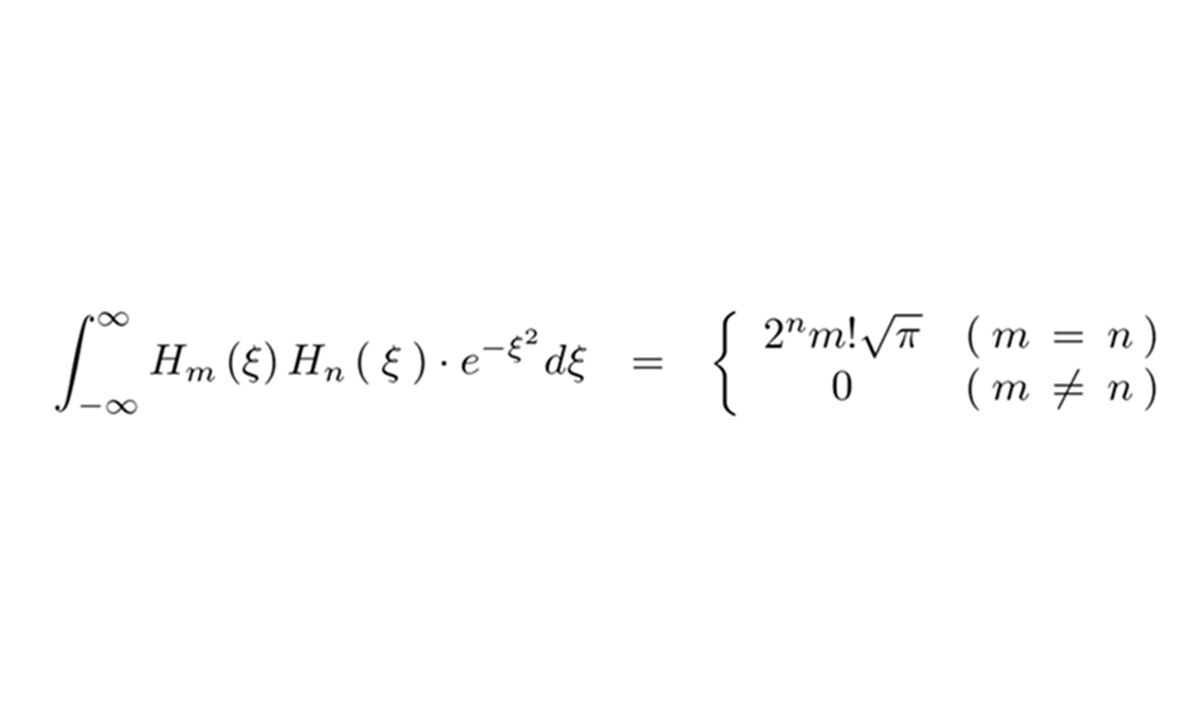
エルミート多項式の直交性
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

エルミート多項式の諸性質
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。

