ラプラス方程式とは

2階線形楕円型偏微分方程式

ラプラス方程式とは、2階の線型楕円型偏微分方程式のことであり、ある領域内において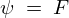なる境界条件を満たすラプラス方程式を求め、それによりさまざまな解析解を導くことを目的とします。

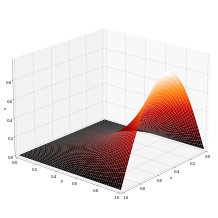
ここでは簡単な例として2次元における長方形プレートの平衡温度分布に関してのその振る舞いを、2次元のラプラス方程式によって考察していきます。

ラプラス演算子

それぞれの座標とした３次元座標空間において２階の偏微分作用素を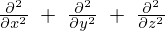とし、この作用素を次のようにおきます。

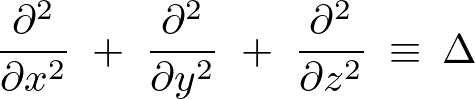
ここでナブラと呼ばれる次のもの、

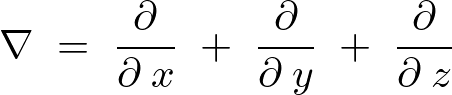
これを使って表せば上記式の２階偏微分作用素式の右辺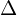は次のようなものになります。

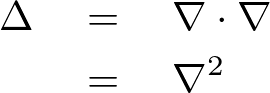
ラプラス方程式とは、考えうるそれぞれの次元において付与される作用素の2階微分に関して、そのラプラス作用素を用いて表現すると次のようなものになります。

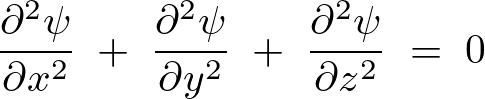
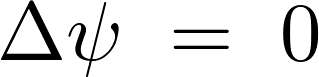
上記式をみてわかるようにラプラス方程式には時間に当たる変数が含まれていません。それにより時間によって変化しない定常状態を表します。

時間を反映した変数がないため、このために初期条件はなく、次に示すような境界条件だけが必要となります。

ディリクレ境界条件

ここでは長方形プレートとみなした場合の以下のようなもの、

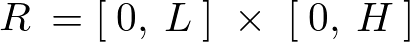
とした、2次元でのラプラス方程式の考察をしていきます。

境界条件として次のようなものとします。

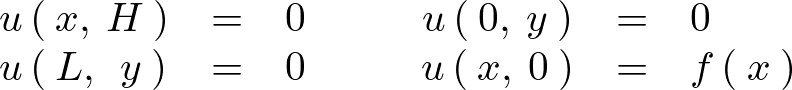
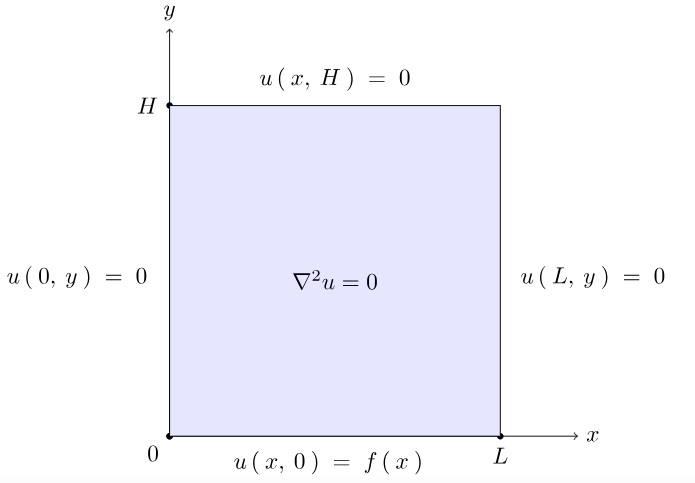
変数分離

ラプラス方程式を解いて行くためにまず変数分離という作業を行います。

変数がと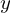の2つになるので関数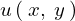に対して次のようにそれぞれの関数を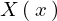と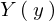に分けて偏微分していきます。

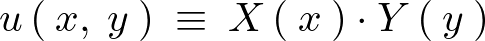
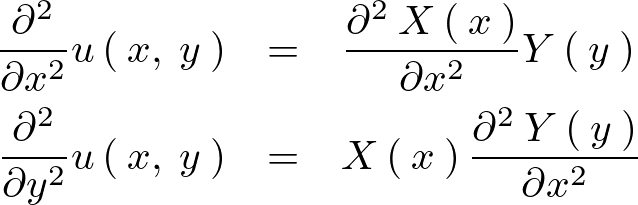
これにより次のような形にできます。

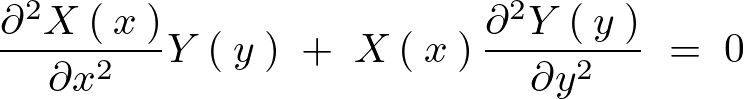
上記式を右辺左辺に分けます。

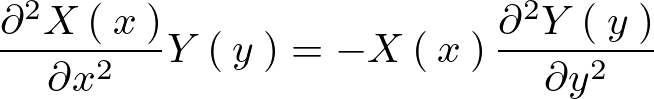
ここで変数分離を行います。

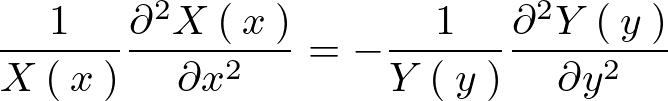
このような変数分離形を行えば左右それぞれの辺を定数におけるので、その定数をとおきます。

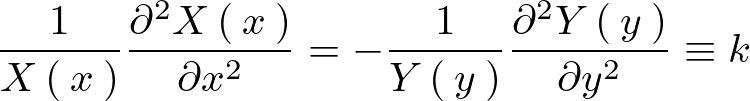
そうするとそれぞれの変数において次のような表現ができることになります。

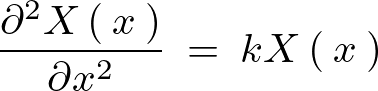
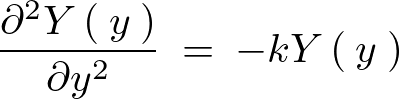
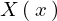の解の導出

まず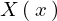の方程式から求めていきます。

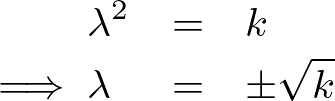
これにより一般解は定数をそれぞれ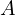、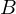とおけば次のようになります。

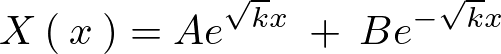
この求まった式において先程の境界条件を課して計算していきます。

まず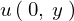より、

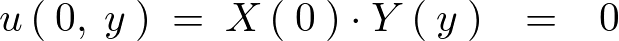
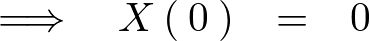
これを一般解に代入します。

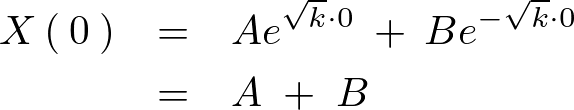
となるのでまず一つ目に関して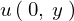というような境界条件から以下のような式が求まります。

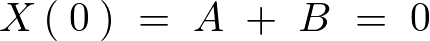
次に境界条件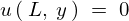を考えます。

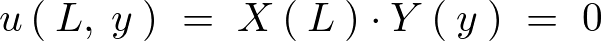
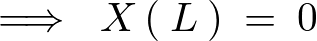
同様にして先程の一般解に代入します。

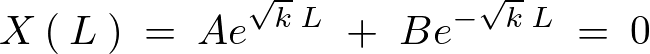
これより以下のような連立方程式が求まります。

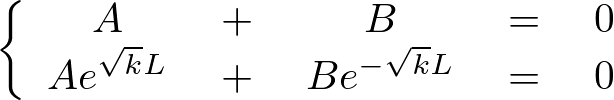
ひとまずここで上記式において自明でない解を持つかどうかの条件の確認をします。

ある連立方程式において非自明な解を持つ必要十分な条件としては次のようなものになります。

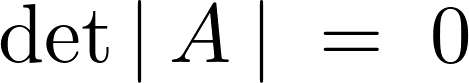
これを当てはめて行列式を組み立てると次のようにおけることになります。

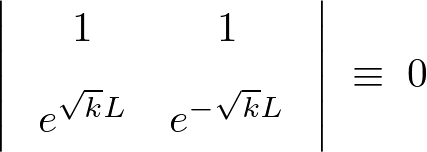
上記行列式の左辺を計算していきます。

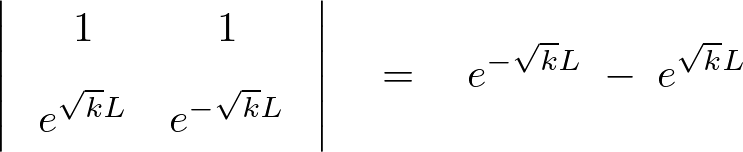
この求められた上式の右辺が次のようになる条件を考察していきます。

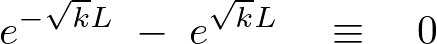
これを計算していくと、

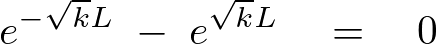
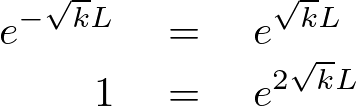
のようになります。

さらに今度はこの求められた式のようになるような条件を考えます。

今ここでオイラーの式を思い出すと、

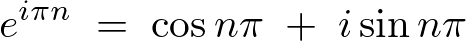
一般的に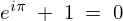より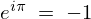ですが、ここで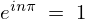となるようなものを考えます。

コサインの性質により、

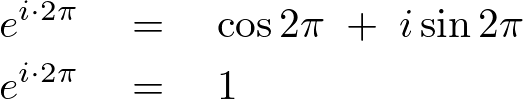
この結果により、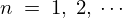、とおいたならば次のような関係式が導かれます。

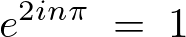
これを比較代入します。

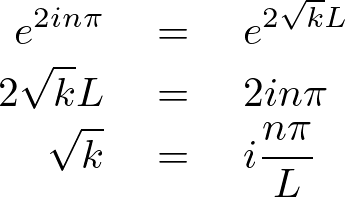
これにより解としての次のような条件が求まることになります。

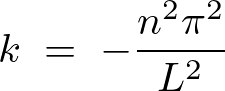
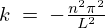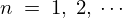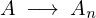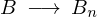としたとき先ほどの連立方程式は自明でない解を持つということになります。このとき方程式のにあわせて定数を、および、そして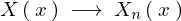とおきます。このようにして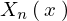は次のような式になることが考えられます。

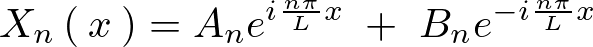
ここで再度オイラー式を思い出すと次のようなものでした。

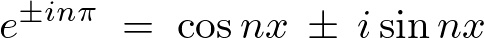
これを使えば先程の求められた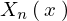の式は次のようになります。

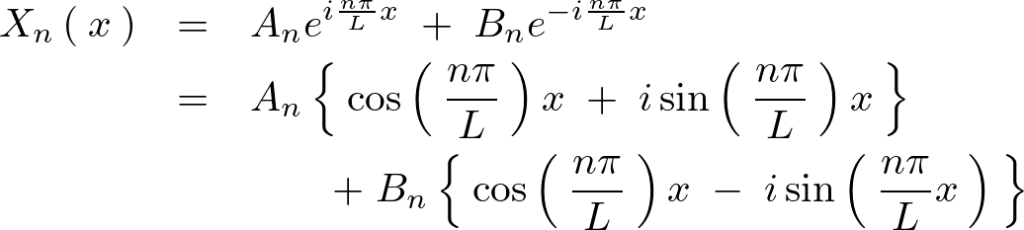
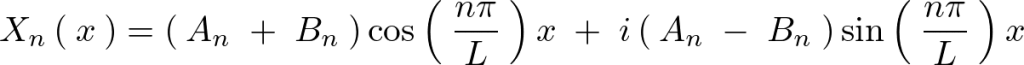
ここで先ほどの求められた条件式、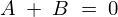より、

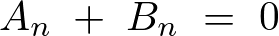
から、求められた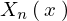の式は次のようなります。

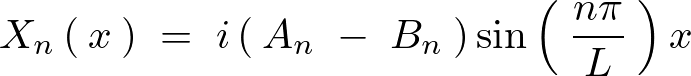
このようにして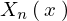に関する方程式が求まりましたがここで見やすさのために上記において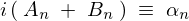とおいて次の形にします。

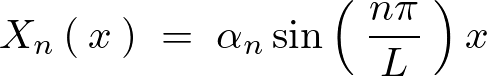
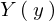の解の導出

次に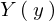の導出を行います。

変数分離により求まった式は以下、

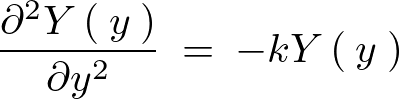
この式より、

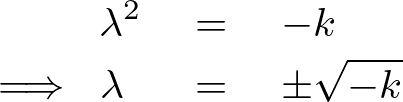
これから一般解は次のようになります。

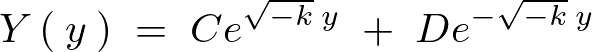
境界条件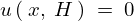より、

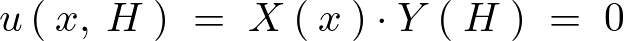
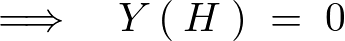
この結果により次のような式が求まります。

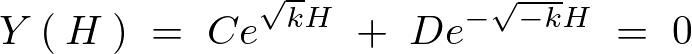
この式の定数部分に関して次のように求めていきます。

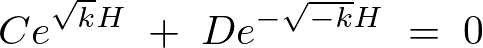
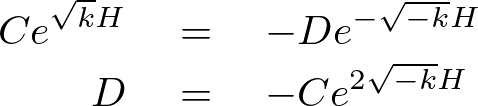
これを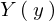に代入して式変形をしていきます。

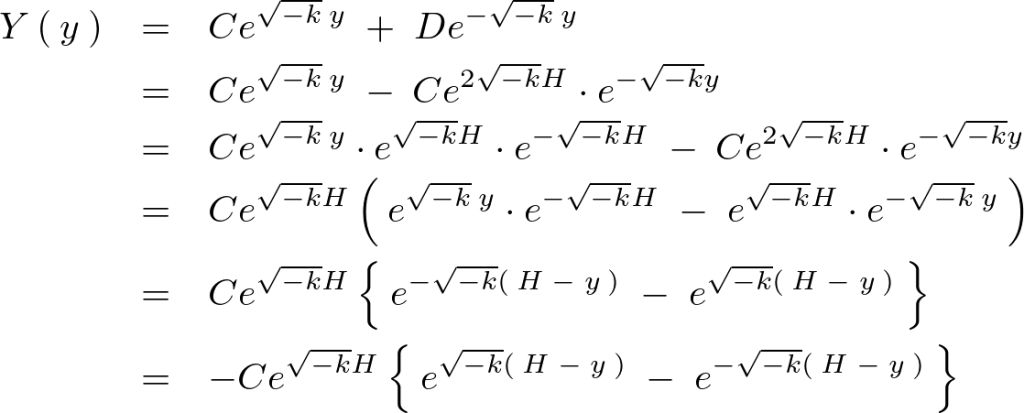
ここでシンチ、またはハイパボリックのサインと呼ばれる次の式、

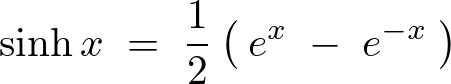
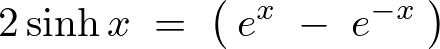
これを当てはめれば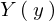の式は次のようにおけることになります。

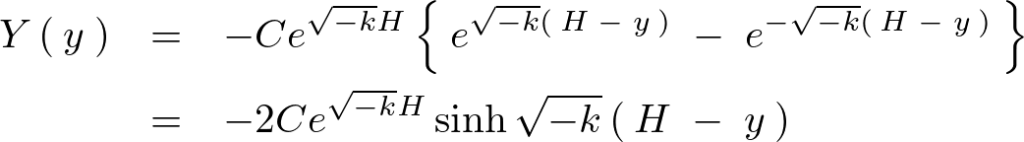
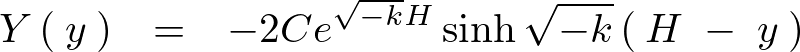
以上のようにして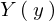の式が求まりましたがここで再度境界条件を引き出します。

境界条件の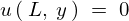から、

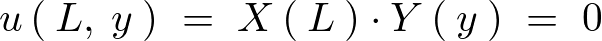
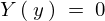が導かれるので代入します。

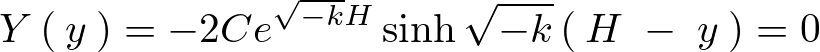
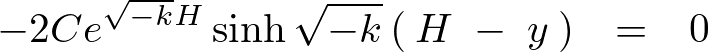
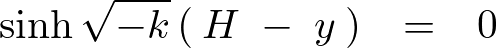
上記の式の左辺に関して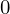となる条件の再確認をします。

先ほどの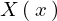で求まったの条件とは次のようなものでした。

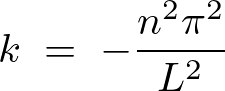
これを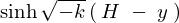の式に代入すると、

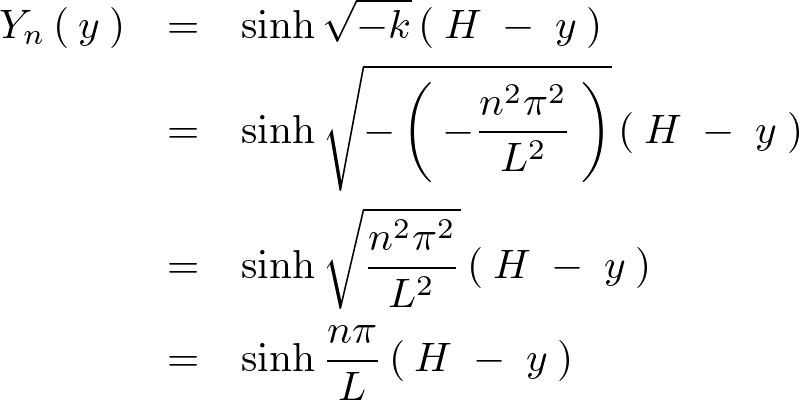
は、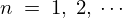であったので必然的に条件は成立しています。

なので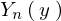に関しての式は以下のようになります。

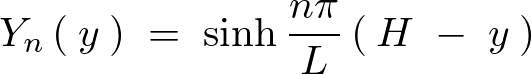
これで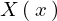、および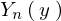に関しての式がそれぞれ求まったので、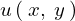に代入していきます。

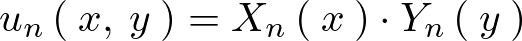
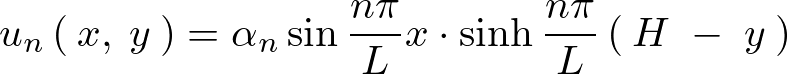
さらに上記の求まった式に関しての線形結合について考察していきます。

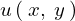は線形微分方程式であり独立な解どうしであったとしてもそれらを重ね合わせたものもまた同様に線形微分方程式の解となります。

線形の重ね合わせの原理を考えた場合、和による結合式もまた同様に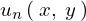の解として成立すると考えれば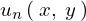の式は以下のように表現することができます。

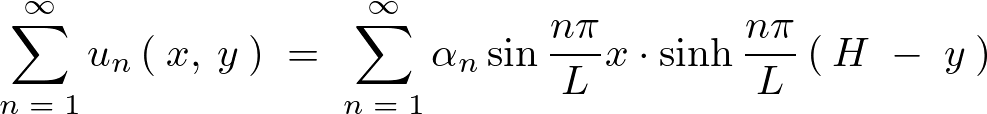
境界条件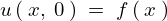の考察

最後の境界条件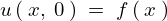について考えます。

上記の求まった式に対してこの境界条件を当てはめると次のようになります。

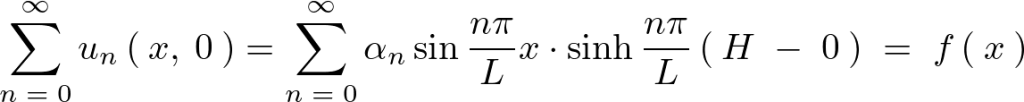
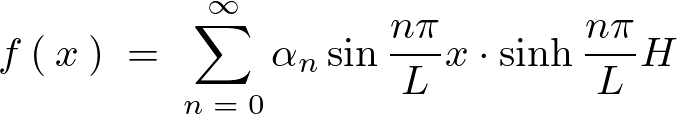
フーリエ級数展開式の適用

さらにここで上記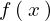の式に対して変数が含まれていない部分を次のようにおきます。

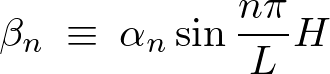
そうすると求められた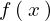の式は次のようになります。

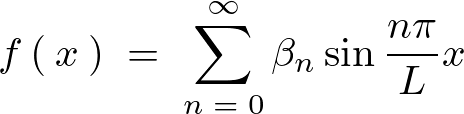
ここでいったんフーリエ級数のサイン項を思い出せば、

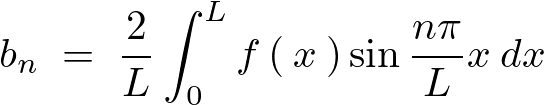
であったのでこれを比較対応させると次のようになります。

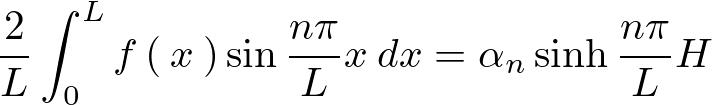
整理すると、

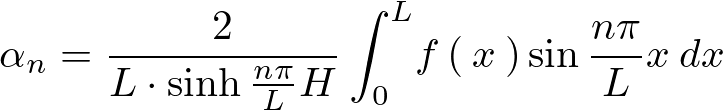
まとめれば先の境界条件をみたす解は以下のようになります。

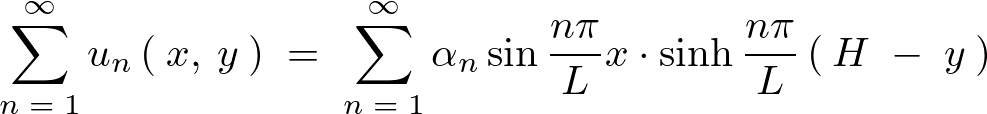
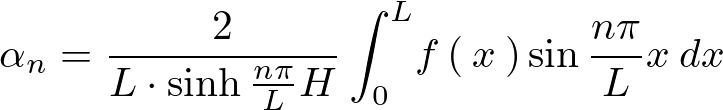
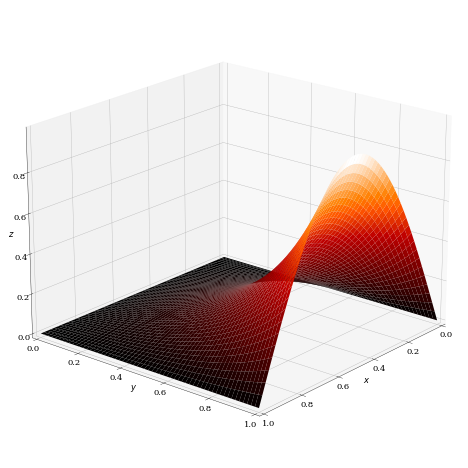
画像は上記求められた解を3次元的な形で描画したものです。pythonによって作成されています。