波動方程式
波動方程式とは
２階の偏微分方程式における境界値問題
２階の偏微分方程式における境界値問題として、ここでは波動方程式を取り上げます。
波動方程式とは、波動の変位に関して時間と座標に関する変数を独立変数としてとらえることのできる定数係数型偏微分方程式（双曲線偏微分方程式）であり、この方程式における境界値に関する問題を、半区間におけるフーリエ積分表示などを使って解いていくことを考えていきます。
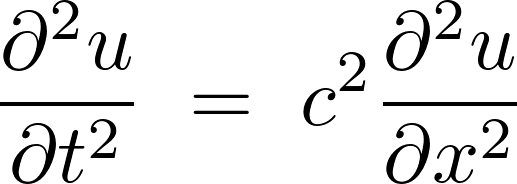
境界条件
境界条件としてまず次のように置きます。
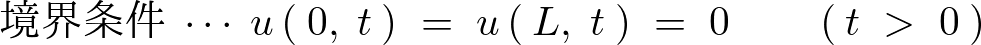
さらに弦の初期条件とその速度微分を次のように与えます。
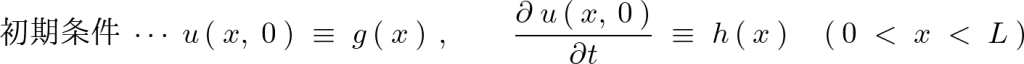
ここで上記の
を、距離と時間の２つの変数を含む次のようなもととします。
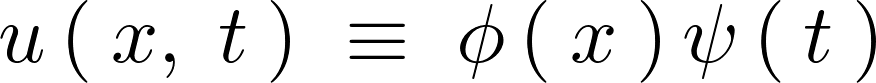
波動方程式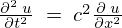
に対してそれぞれ当てはめれば、
左辺
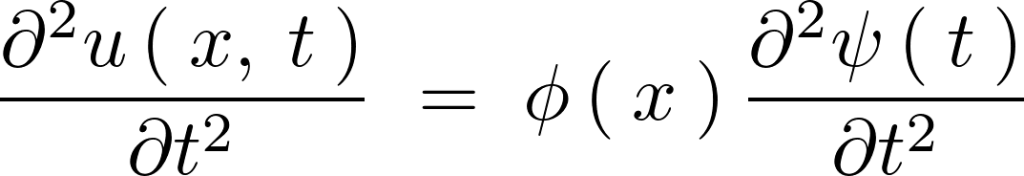
右辺
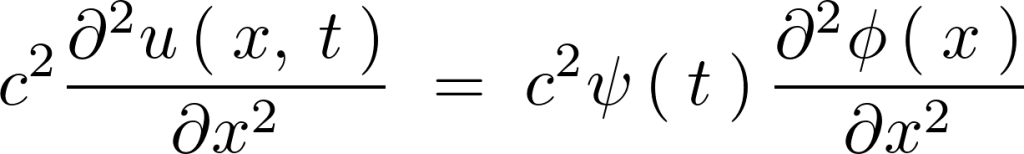
これらにより、
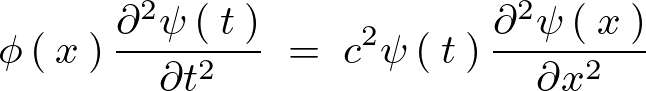
上記式に対して変数分離を行うと、
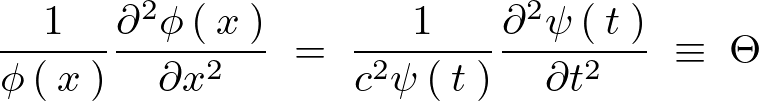
それぞれの変数に分離できたのでまずは
のほうから考えていきます。
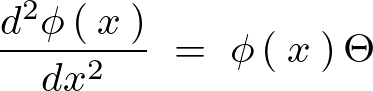
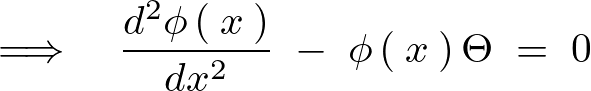
次のような条件を考えます。
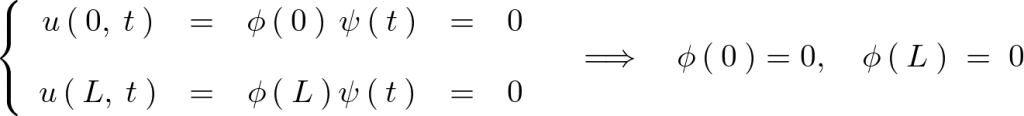
といった条件を満たすものを求めます。
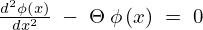の解で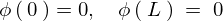
の式を満たすものは次の3種類が考えられます。
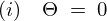のとき
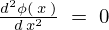という条件での一般解を求めます。
以下のように積分を実行していきます。
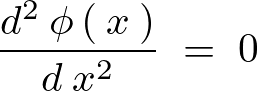
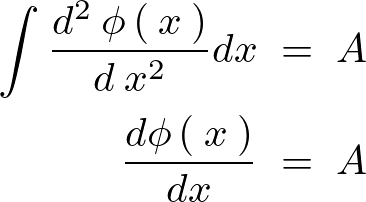
さらに積分を実行していきます。
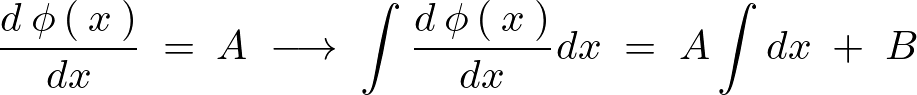
よって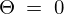
のときの一般解は以下のように求まります。
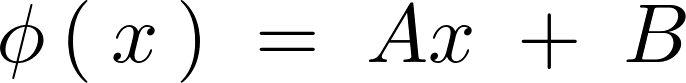
条件より、
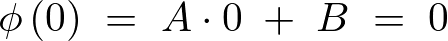
さらに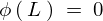
の条件、
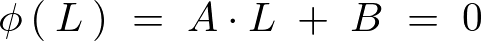
も考慮すれ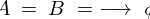ば
は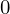
となり意味がありません。
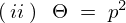のとき
一般解は、
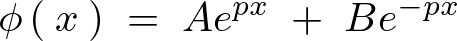
となるので条件より、
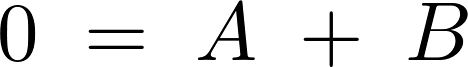
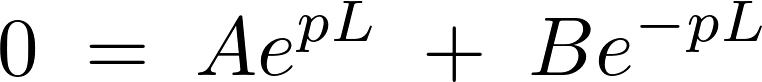
となります。
この場合も再び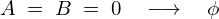
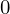はとなるので
と同じように解として意味がありません。
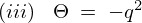のとき
最後の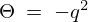
を実際にやってみると、
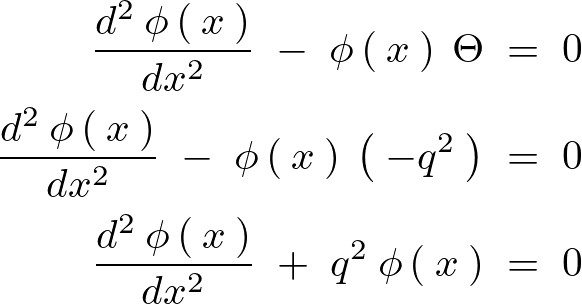
よって以下のように求まることになります。
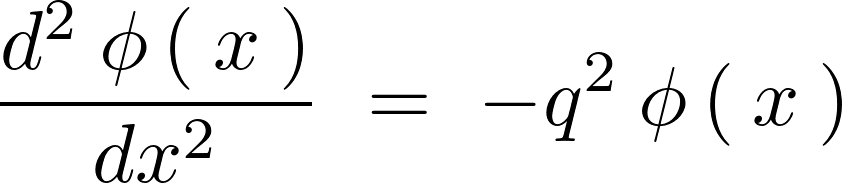
このためこの式の特性方程式は以下のような複素数解になることになります。
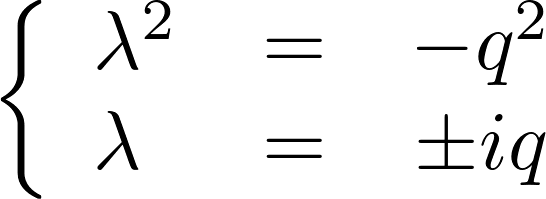
実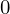数部は、虚数部は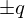
なので特性方程式は、
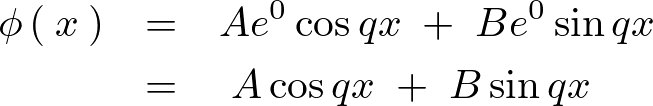
条件より、
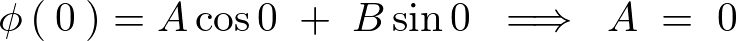
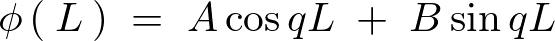
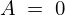なので、
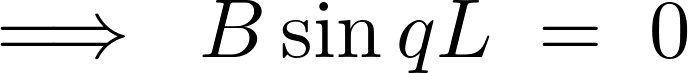
ここで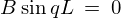
であるためには
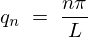という条件が必要になります。
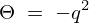の場合は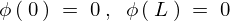
の条件を満たす
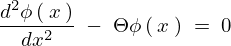の解として、
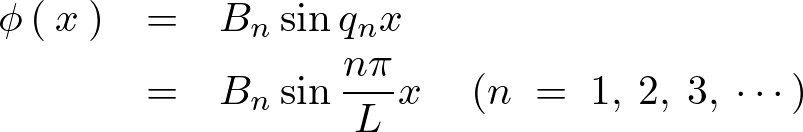
さらに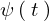
に関して、
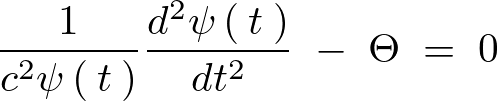
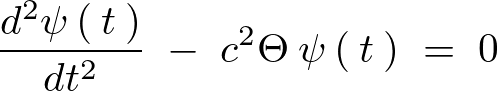
意味のある解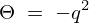を代入すれば、
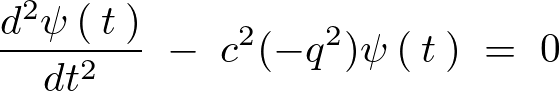
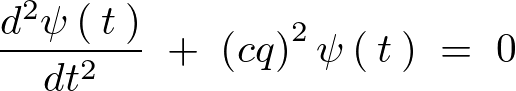
先ほどの結果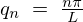
を代入すると、
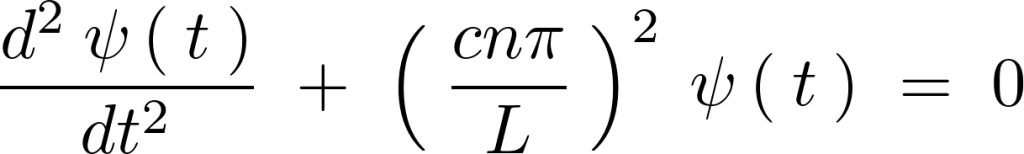
この方程式の解を求めるために同様にして特性方程式を導くと、
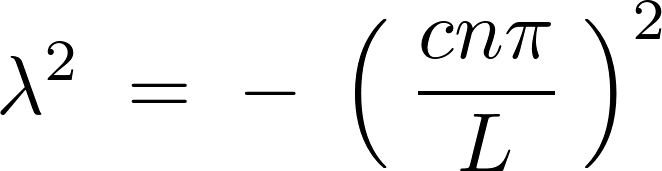
より、
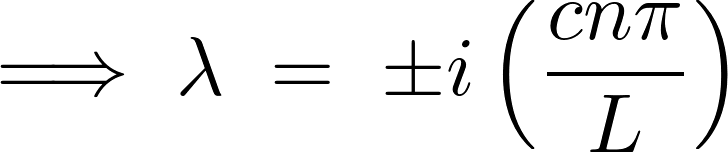
実数部が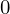で虚数部が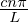
なので、
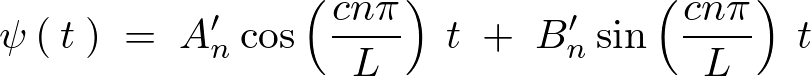
これらの結果をそれぞれ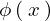
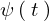およびとして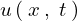
に代入すれば、
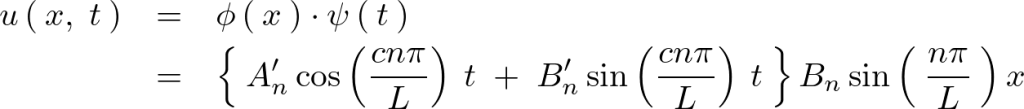
ここで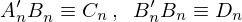
と置けば、
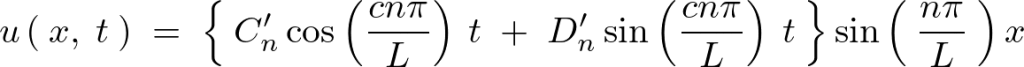
上記式中の
はを除く整数であり異なるに対してもまた同様に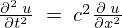
の解として成立します。
また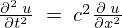は線形微分方程式であり独立な解どうしであったとしてもそれらを重ね合わせたものもまた同様に線形微分方程式の解となります。
線形の重ね合わせの原理を考えれば、
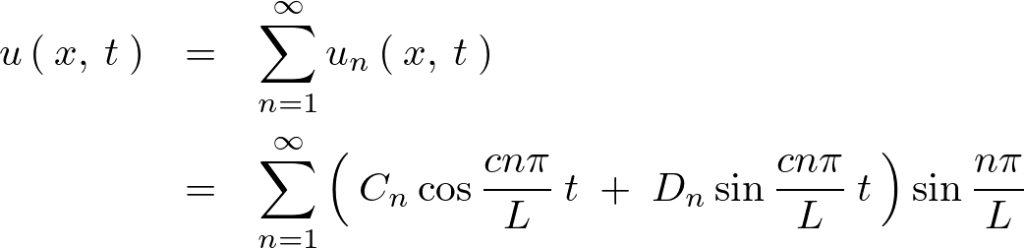
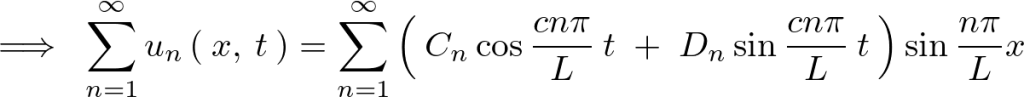
初期変位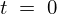
のときに、
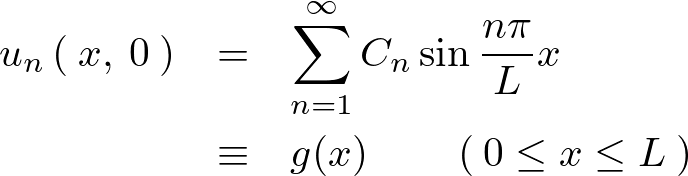
ここで式を見やすくするために次のように置きます。
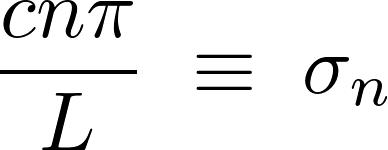
フーリエ級数の半区間の展開において奇関数での拡張を思い出せば、
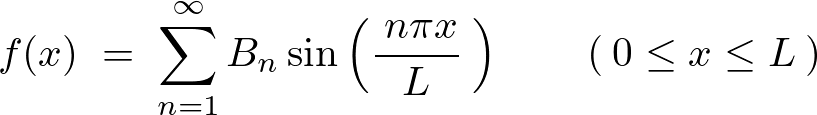
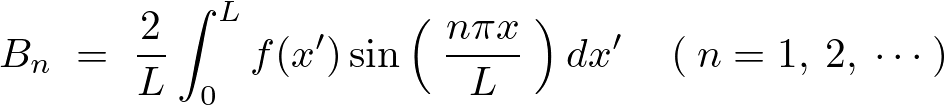
これを使えば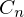
、および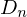
は以下のように求まります。
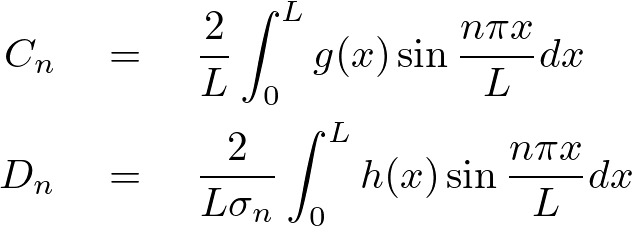
上記を代入すれば以下のような一次元波動方程式の解が求まります。
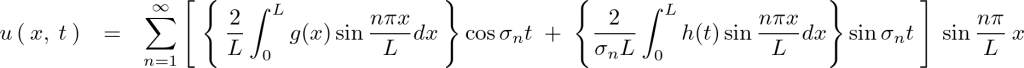
波動方程式
波動方程式とは、波動の変位に関して時間と座標に関する変数を独立変数としてとらえることのできる定数係数型偏微分方程式になります。
熱伝導方程式
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
コリオリの力とは
フランスの科学者で軍属でもあったガスパール・ギュスターブ・コリオリ
初歩的な力学の分野において慣性系に関する話の中にコリオリの力というものがあります。
この“コリオリ”とは人の名前であり地球が回転することによっておこる見かけの運動力を、回転座標上で移動したときの移動方向と垂直な方向に受ける慣性力の一種を数式で表現したものになります。
一般的にこのコリオリという人物は科学者という記述が多いのですが実は軍人でもあったことはあまり知られていないようです。
北半球において大砲を撃ったとき、その弾道が標的よりもわずかに右にずれることを数式によって説明した人物ということで自衛隊でも多少知られた存在らしく、話の小ネタとして話題になることもありました（おそらく重迫撃砲(ヘヴィモータ)などではコリオリの力による弾道補正が必要になるためだと思います）。
回転座標で運動する物体
円運動の角度を
、周囲に沿った距離を
、ボールの速度を
、慣性力を
とおくと、
上の図は、矢印の通りに回転させた円盤を真上からみたものであり、中心から外側へ投げた球があたかも右のほうへずれたように見えるその様子を表したものです。中心部分にいる人物は図の
の方向へ投げたつもりが
のほうへまるで曲がって投げたように見えてしまいます。
はは動径方向に垂直な方向に働く慣性力とし、一定加速度での移動距離は
の形で表せるので、
この力をコリオリの力と呼び、回転座標系で運動する物体に加わる慣性力のことを言います。
この力を実際に数式を使って具体的に表現してみましょう。
左の座標系が3次元での回転、右の座標系の図が２次元での回転を表したものになります。
これより回転座標系において時間変化した角度をとすれば以下のように表せます。
または、
これを時間で微分します。
上記式を再度時間微分します。
力
と
の間の関係は次式で表されます。
さらに
系（慣性系）では次のような運動方程式、
が成り立つので上の式の結果を用いて
を表せば、
これらを代入し
系の座標について整理すれば、
は回転系座標から見た加速度運動で、運動の原因となる力としてのほかに2つの力が加わった形であり、右辺第2項、第3項は見かけの力（慣性力）を示しています。
右辺のそれぞれの意味は、
| 右辺第2項（コリオリの成分） |  |
| 右辺第3項（遠心力の成分） |  |
を示しています。
回転座標系をまとめてみると次のようになります。
慣性系に対して運動する座標系
| 1. | 等速度運動する座標系は慣性系となる（ガリレイ変換） |
| 2. | 加速度運動する座標系は非慣性系（見かけの力＝慣性力）を考える
 |
| 3. | 回転運動をする座標系は２種類の見かけの力を考える
|
これらを踏まえて今度は長距離射撃におけるコリオリ弾道軌道計算を考えていきましょう。
次回に続きます。