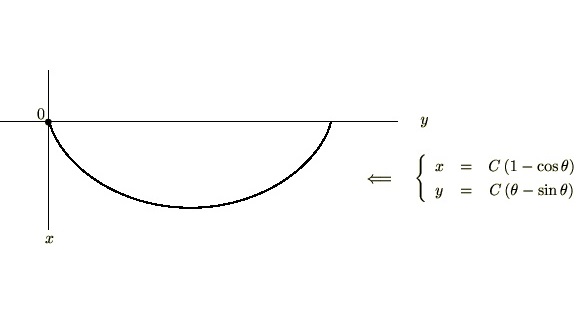懸垂線
懸垂線とは
ロープや糸などの紐の類をその両端を固定して吊り下げたものを懸垂線などといいます。これは物理的なポテンシャルが最小になるときのものであり、ここではそれを表す方程式をオイラーの式を使って求めるのですがいままでのやり方だとちょっとうまくいきません。そこで途中の式で全微分の公式を使います。こうしたやり方は物理現象を数式によってとく際にたまに使われる数学テクニックになります。
たとえば一様な重力場中の質点の力学的エネルギー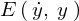 は時間によらず一定(
は時間によらず一定(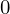 になる)であることの証明や、壁に立てかけた棒の運動を数学的に説明するときなどに使われます。
になる)であることの証明や、壁に立てかけた棒の運動を数学的に説明するときなどに使われます。
とりあえず実際にやってみましょう。
紐の長さは とします。
とします。
微小線要素は先ほどと同じく![]() とします。よって、
とします。よって、
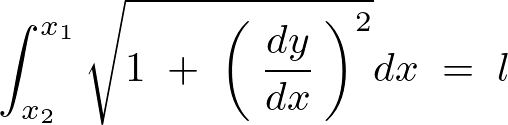
となりますがここで簡単のために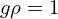 と置きます。
と置きます。
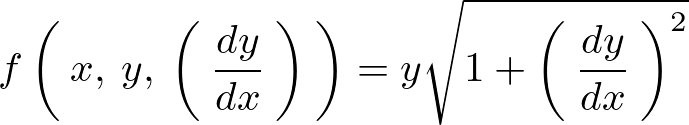
これをオイラーの式に合わせて解いていきます。
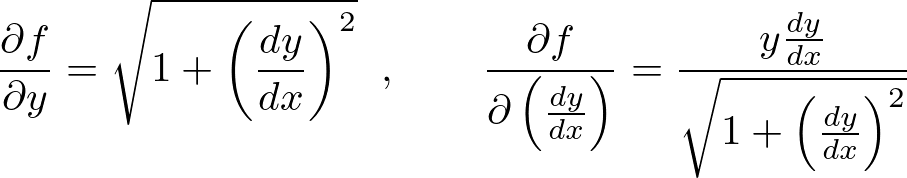
オイラーの方程式、
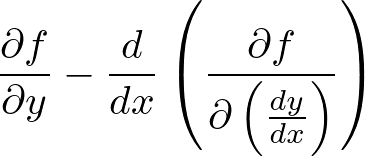
にそれぞれを代入して計算していくのですがそのままの計算を行うと結果が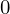 になってしまうのでここでちょっと工夫をします。
になってしまうのでここでちょっと工夫をします。
まず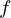 に対して全微分の公式を適用します。
に対して全微分の公式を適用します。
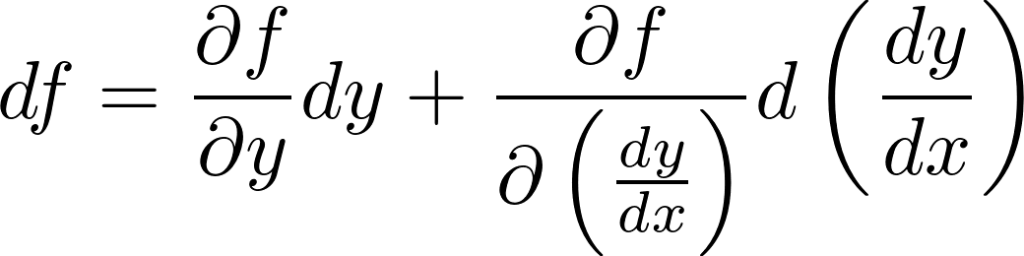
さらにオイラー式の両辺を でスカラ倍します。
でスカラ倍します。
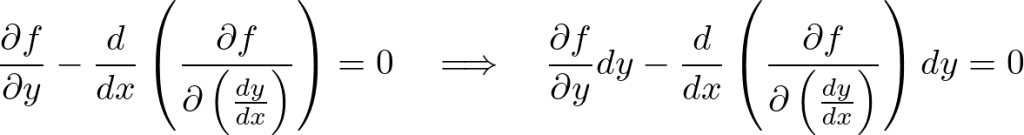
出てきた以下の式、
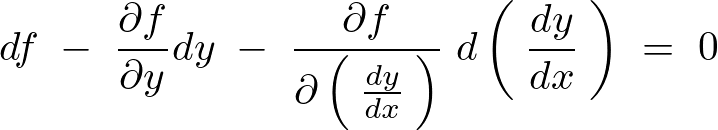
と、次の式、
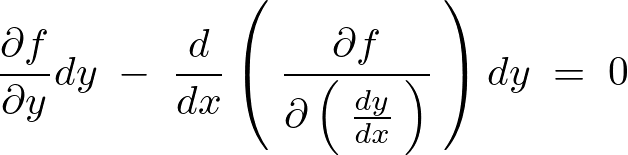
の式を、次のように互いに足し算引き算してそれを変形させていきます。
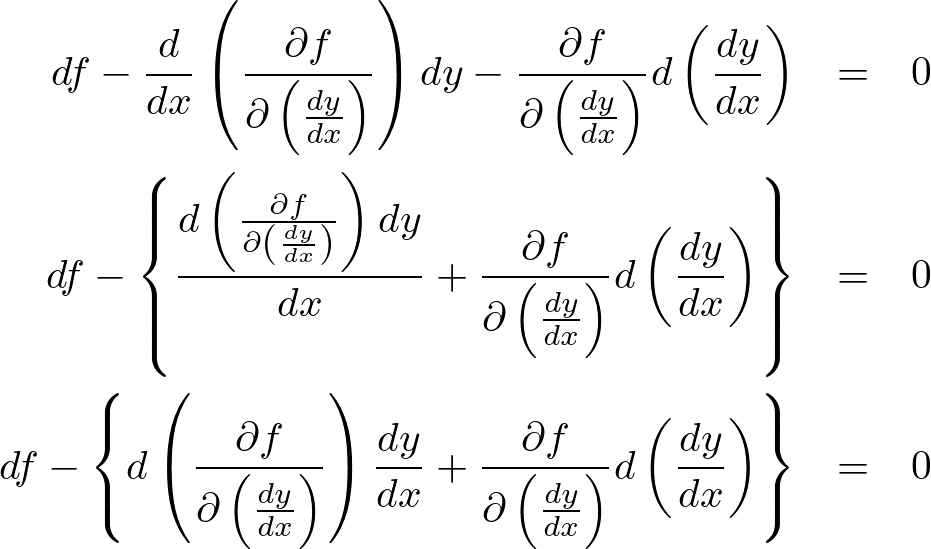
ここで上記式左辺の第2項に関して、積の微分を考えると、
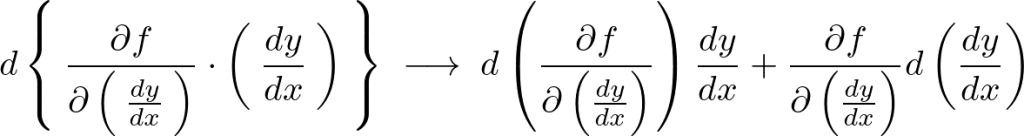
と考えられるので次のような式変形が導かれます。
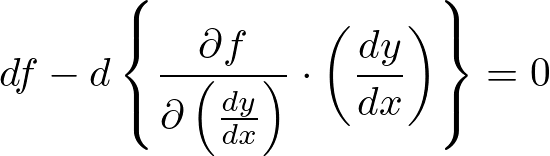
これを積分すれば、
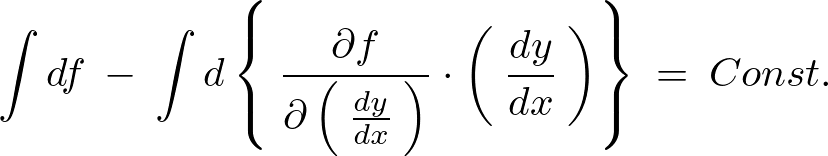
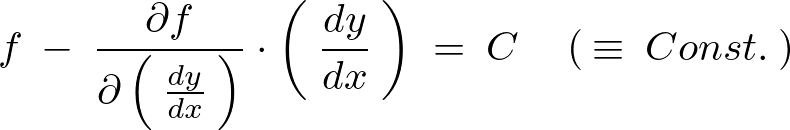
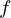 をもとに戻します。
をもとに戻します。
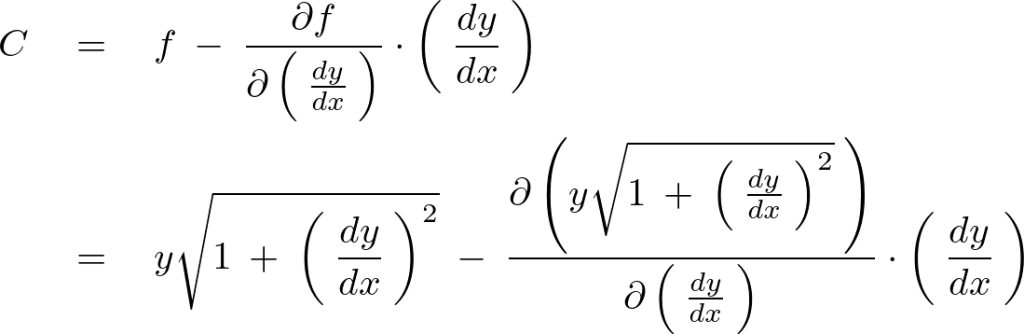
上記式の右辺第2項に関しては次のように連鎖律を使って計算していきます。
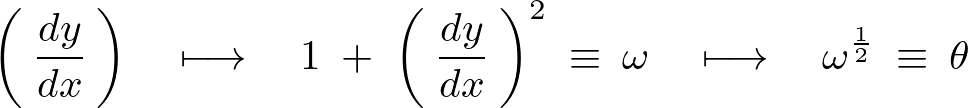
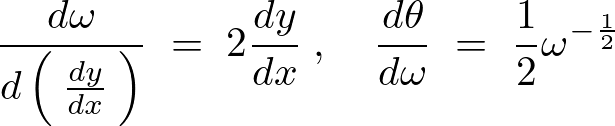
チェインさせます。
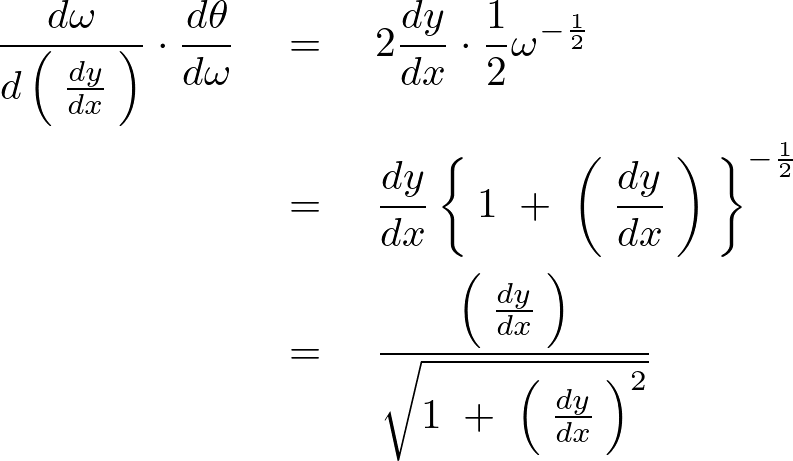
これより右辺第2項の偏微分は以下のように求まります。
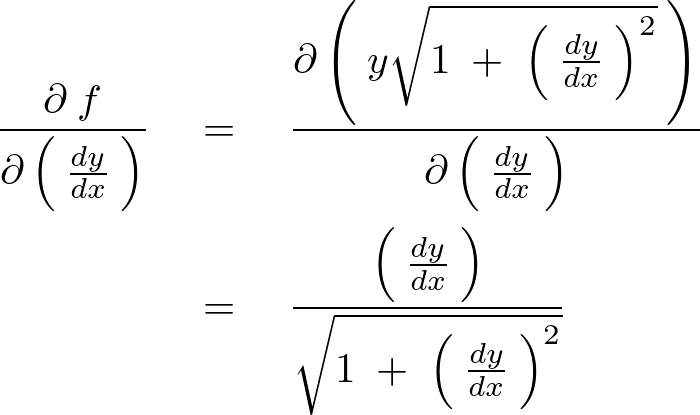
これを代入して計算していきます。
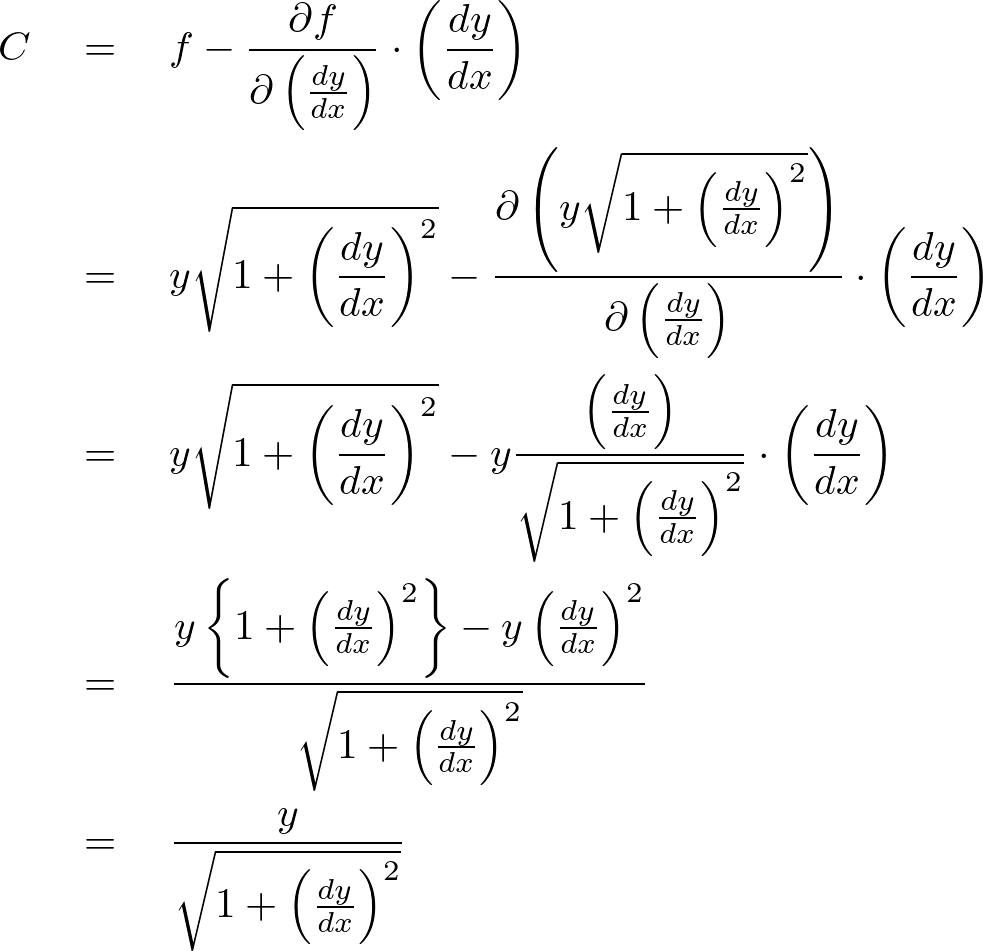
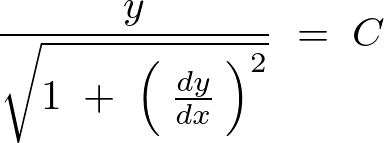
この式をさらに計算していきます。
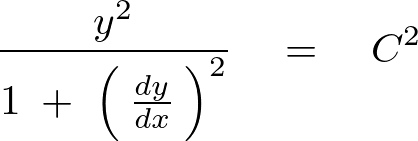
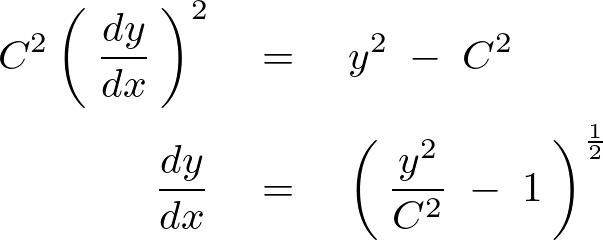
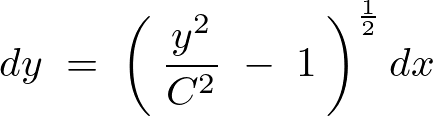
ここで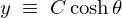 となる変数変換をします。
となる変数変換をします。
これを微分したものは、
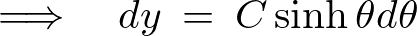
これを代入して計算します。
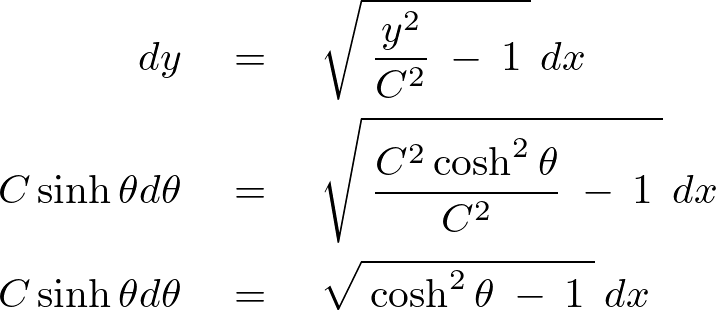
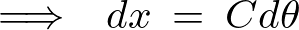
さらにこれを積分して出てきた定数を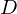 とします。
とします。
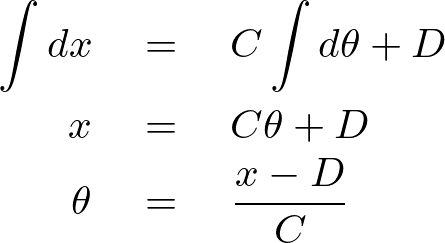
元に戻せば次のように求まります。
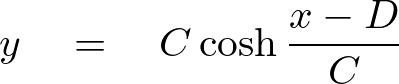
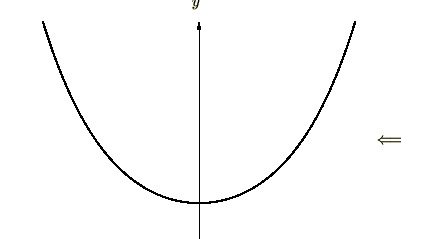
グラフにすると次のようなものになります。
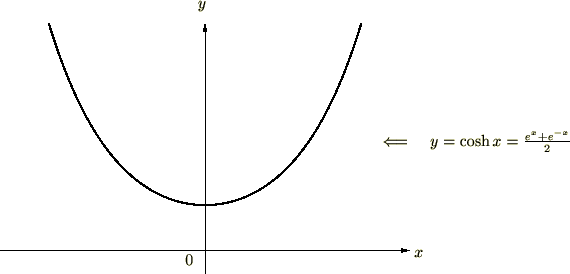
また以下の画像は上記のものを3次元で出力したものになり一般的に懸垂面、またはカテナリーと呼びます。
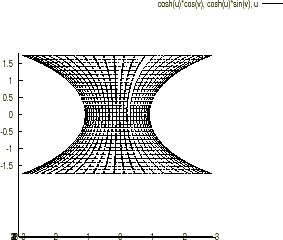
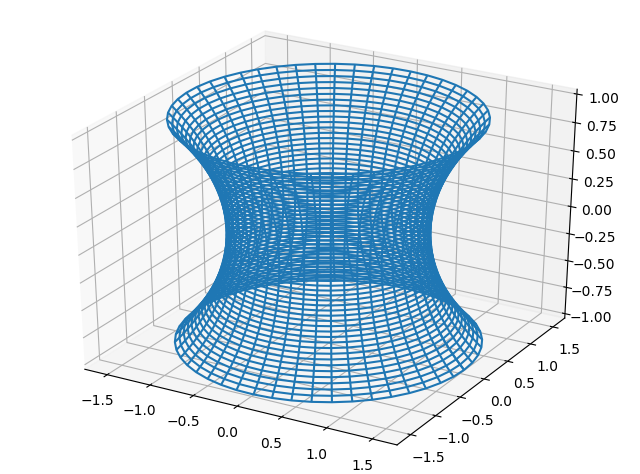
独特な感じがする画像になりますがこれの特徴的なところは平均曲率がいたるところで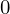 になるというものになります。
になるというものになります。
Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
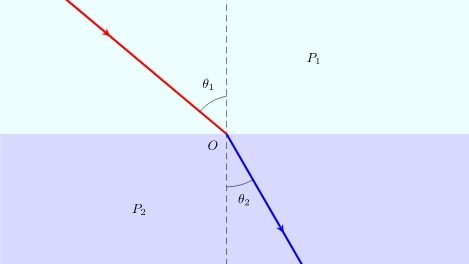
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。