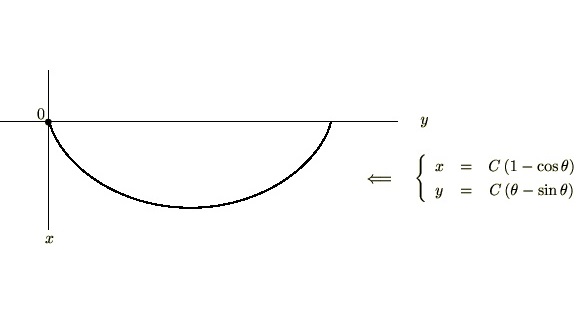変分法
変分法とは
変分法とは、関数とその導関数との微小な変化をとらえた関数の最大値と最小値を見つけることを扱います。変分法におけるオイラー-ラグランジュ方程式は、ある関数の最大値、最小値の関数を見つけたい場合にこの微分方程式を解いていきます。
例としてこのカテゴリーでは、最速降下線問題、懸垂面、フェルマーの原理、古典的等周問題取り上げます。
- 最速降下線問題 2 つの点を結ぶ最短の長さの曲線を考える場合、ある質点が曲線に沿って移動したとき一番短い時間で到達するような曲線はどういったものかというのを考察します。
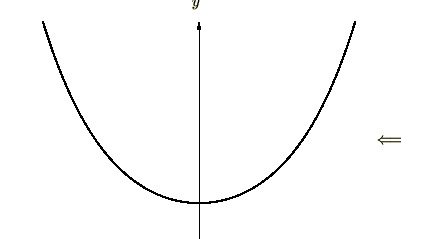
- 懸垂面 ロープや糸などの紐の類をその両端を固定して吊り下げたものを懸垂線などといいます。これは物理的なポテンシャルが最小になるときのものであり、ここではそれを表す方程式をオイラーの式を使って求めていきます。
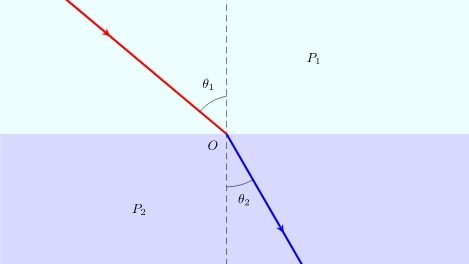
- フェルマーの原理 フェルマーの定理というのは媒質中（屈折率は一定とします）を通る光の２点間の通過時間は極小になるような経路をとるというものです。これを変分法によって求めていきます。
- 古典的等周問題 平面上における閉曲線が囲む面積が最大となるものは何かを考えます
古典的等周問題
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.