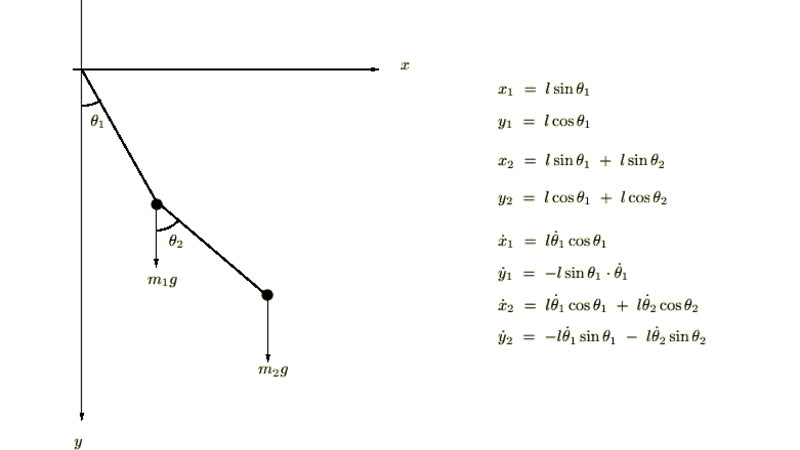連成振動の解①-弦の振動
連成振動の解①-弦の振動
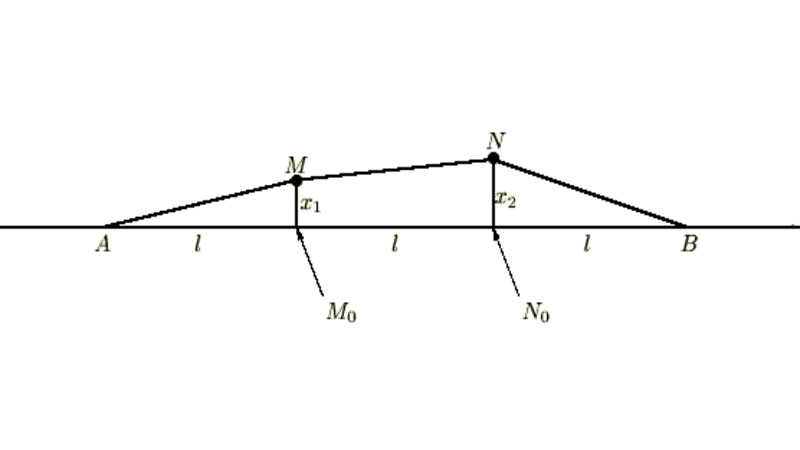
長さ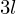 の糸を張力
の糸を張力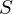 で張っておき、長さ
で張っておき、長さ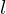 ごとに質量
ごとに質量![]() のおもりを結びつけ、そのおもりは直角方向のみに振動するとします。
のおもりを結びつけ、そのおもりは直角方向のみに振動するとします。
こういった場合のおもりの小振動をラグランジアンを使って求めてみましょう。
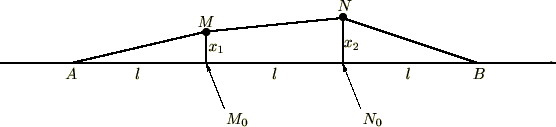
まずそれぞれの糸における直角方向の張力を求めます。
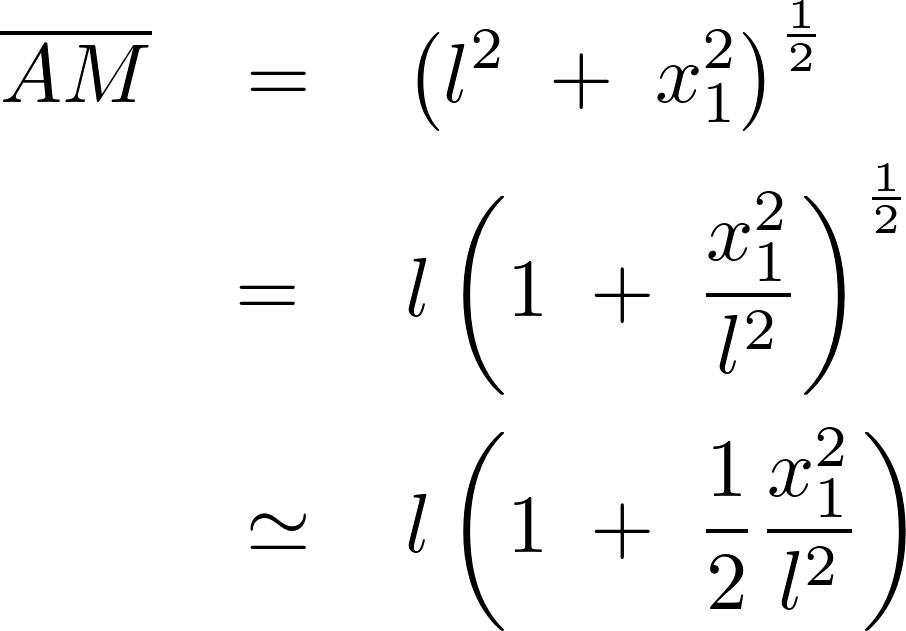
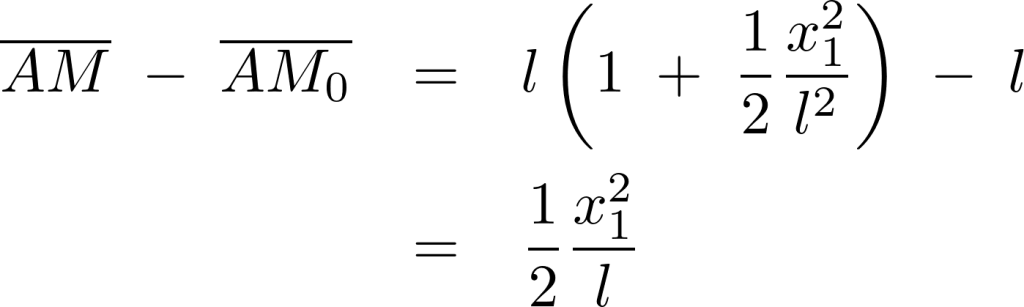
これにより張力は、
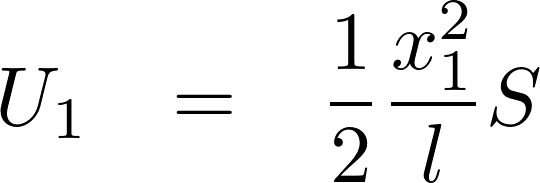
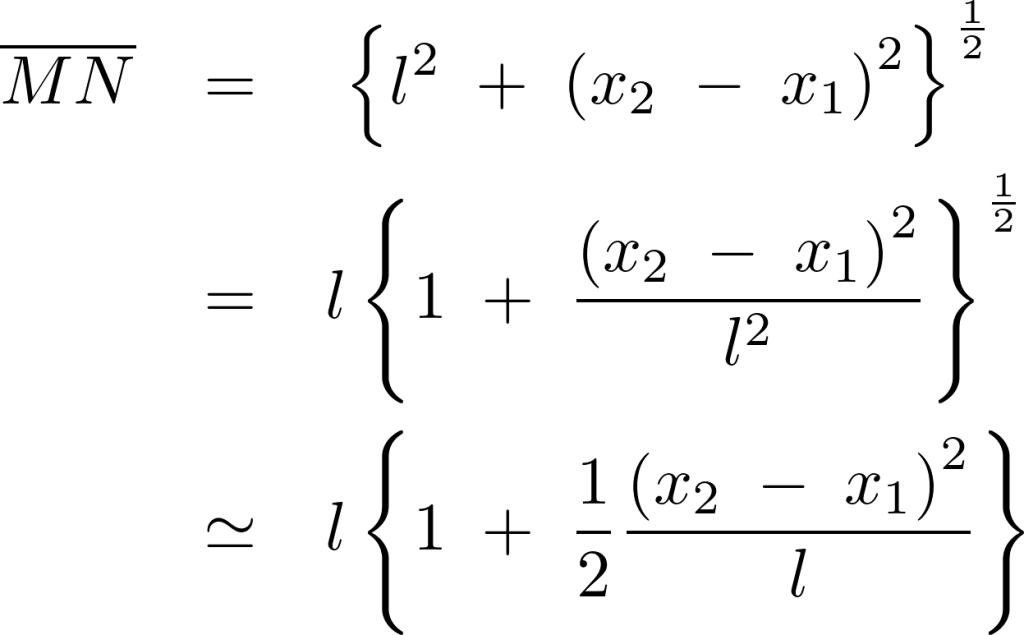
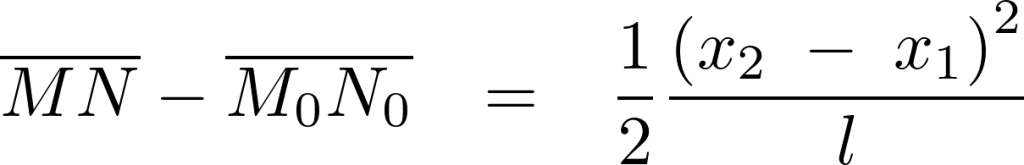
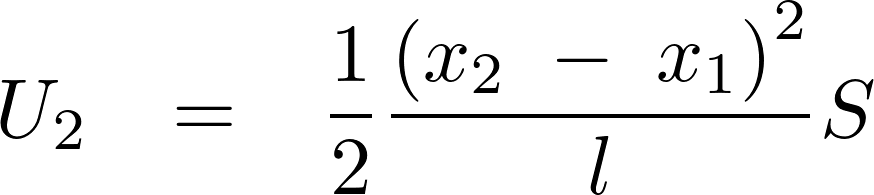
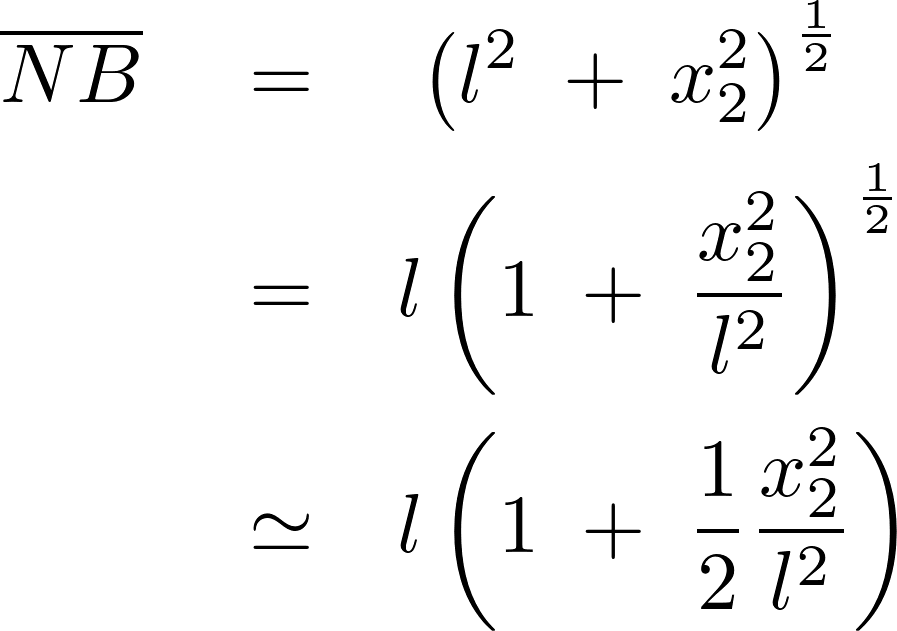
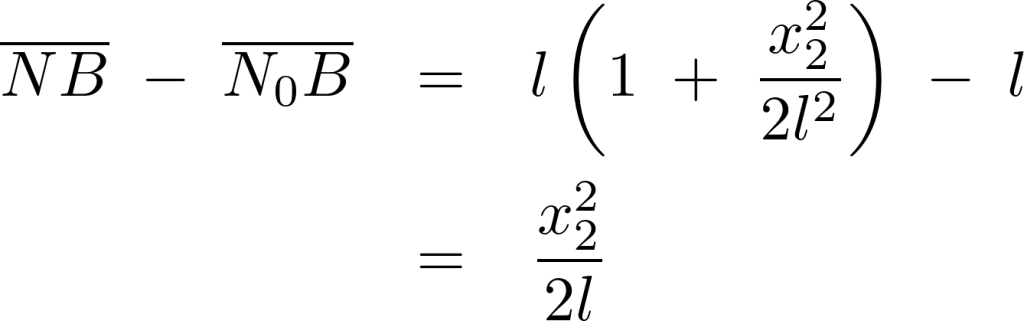
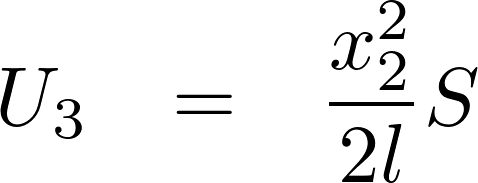
これらの結果によりラグランジアンは次のようになります。
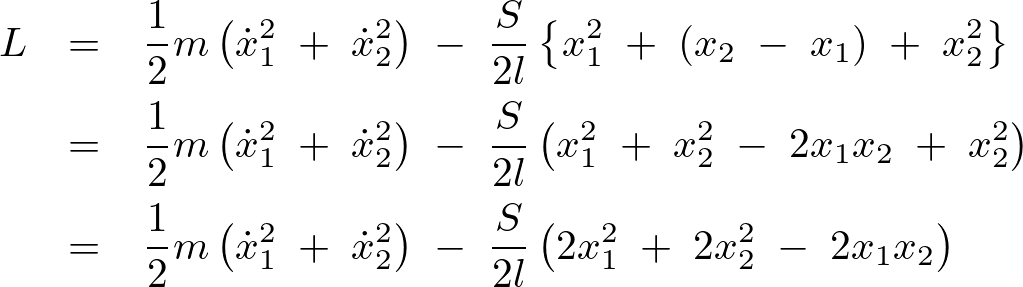
ここでラグランジュ方程式、
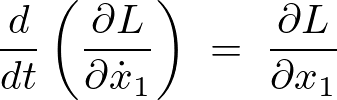
より、
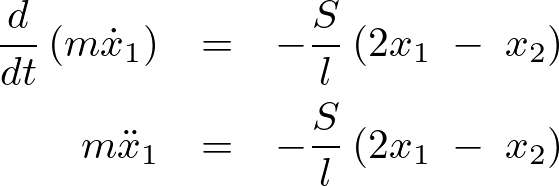
つぎに、
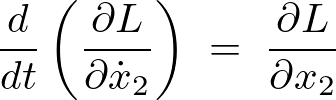
より、

ここで解を次のように置きます。

これをそれぞれ2階微分します。
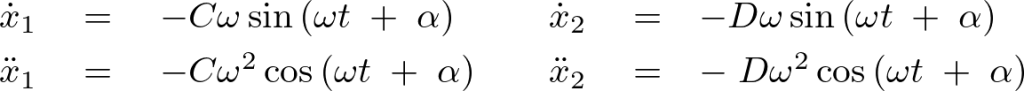
微分前の解とみなしたものと比較すれば、
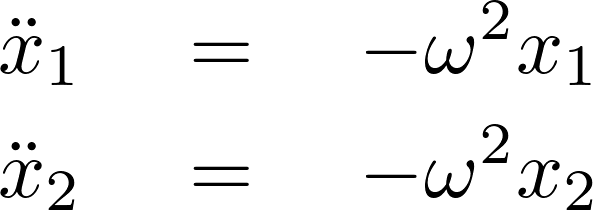
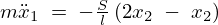 に代入します。
に代入します。
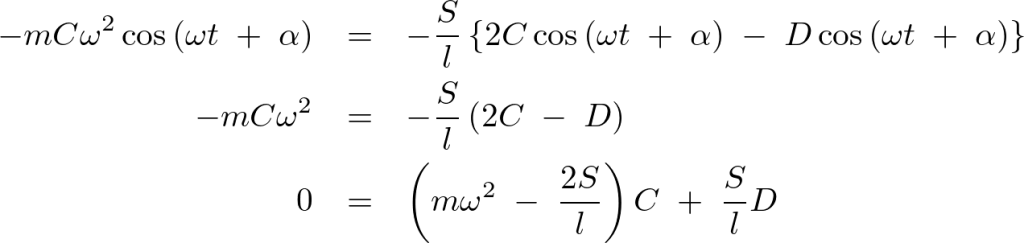
今度は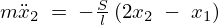 に代入すれば、
に代入すれば、
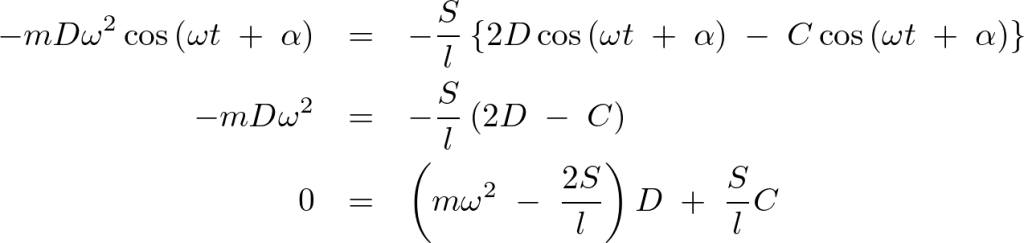
求まった次の式、

と次の式、

の両方の式において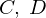 が同時に
が同時に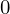 になると運動しないということになり、これは意味がありません。
になると運動しないということになり、これは意味がありません。
上記の式において意味のある解を求めるには、同時に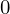 にならないような解を求めなければなりません。
にならないような解を求めなければなりません。
その同時に にならないような条件として次に示すような行列式を使った永年方程式と呼ばれるものを計算する必要があります。
にならないような条件として次に示すような行列式を使った永年方程式と呼ばれるものを計算する必要があります。
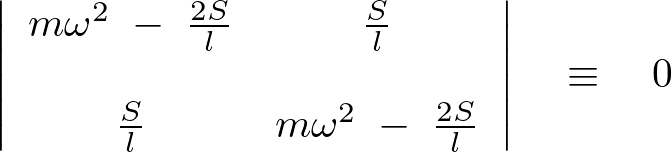
この行列式を解いていきます。
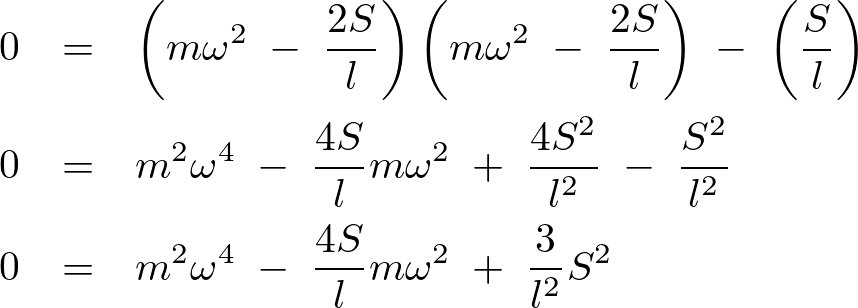
ここで![]() とおくと、
とおくと、
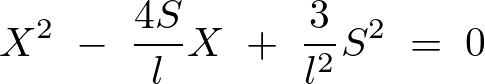
この方程式を以下のようにして分解計算していきます。
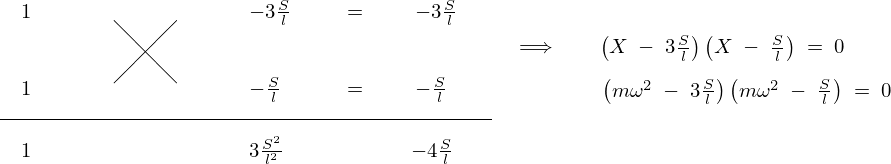
右の導かれた方程式から次のような解が求まります。

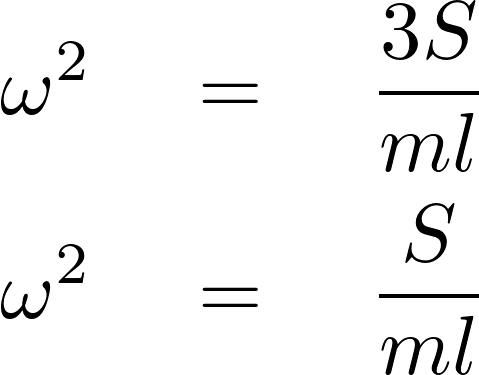
この2つの解が出てくるのでこれをプライムを使って以下のように区別します。

![]() に関して、
に関して、
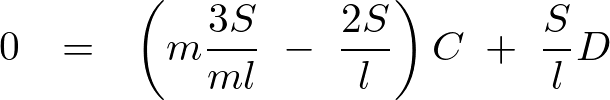
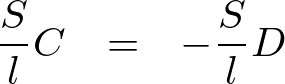
より、
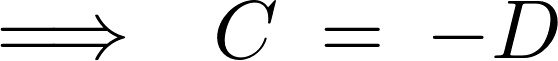
さらに![]() より、
より、
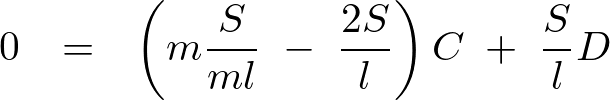
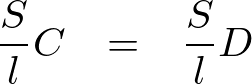
より、
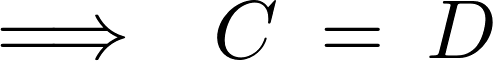
この結果により次のような式が求まります。
まず、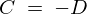 より、
より、
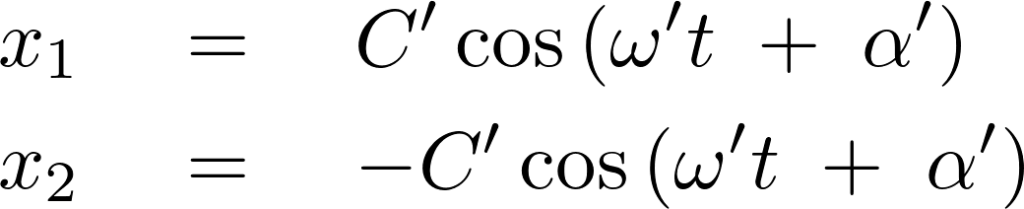
の一組と、
さらに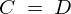 より、
より、
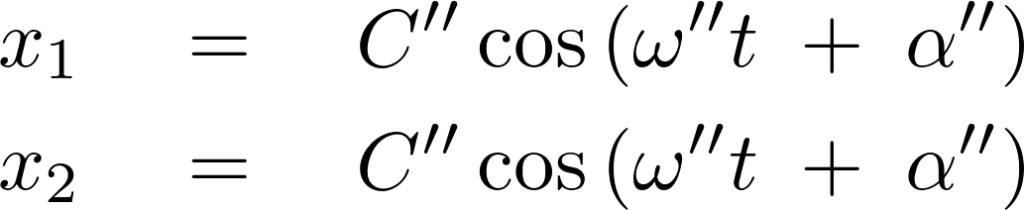
の2組が求められることになります。
これらをそれぞれ加え合わせれば、以下のような解が求まります。
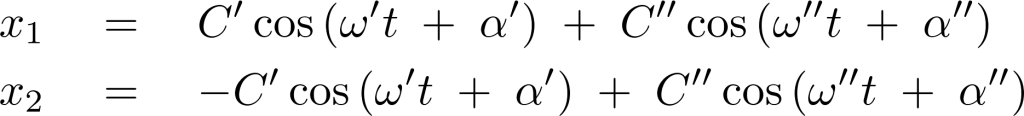
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。