微分方程式
第0章 ━ 微分方程式の概念
微分方程式とは式の中に独立変数とその関数さらにはその導関数を含んでいるものを含めていいます。微分方程式を解くということは与えられている式を恒等的に満たすものを求めることであり、その解には一般解と、さらには任意定数に特別な値を入れて求める特殊解などがあります。西暦1800年前後において微分積分と呼ばれる数学分野がはじまり、それと同時に現実世界における自然現象の因果律を解明するものとして発展してきた学問なんだそうです。
微分方程式は大まかに分けて言うと次の2つに分類されます
- 常微分方程式 常微分方程式-関数
- 偏微分方程式 偏微分方程式-ある関数
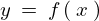 とその導関数
とその導関数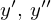 、独立変数
、独立変数微分方程式のいくつかの例
例1
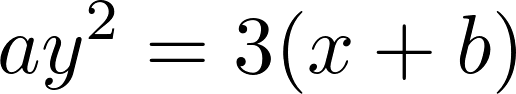
上記の式の両側を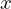 で微分します。
で微分します。
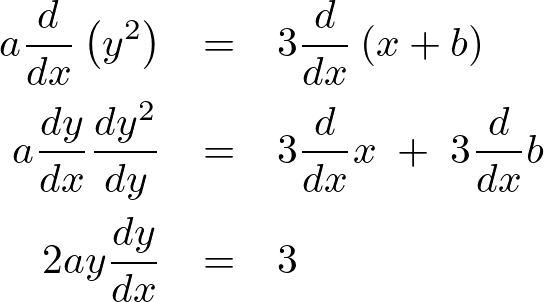
これをさらに微分すると、
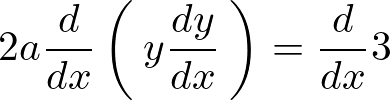
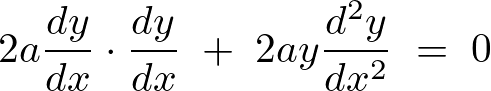
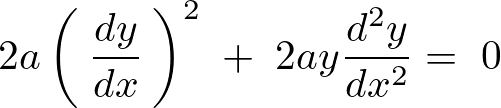
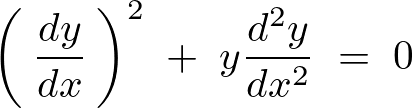
以上のように求まるので整理すれば次のような方程式が求まります。
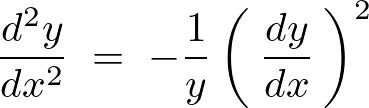
【例2】円に関する考察
次の円について考察してみましょう。
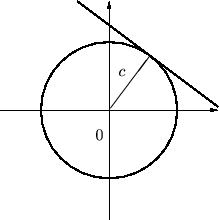
この円に関しての方程式は、
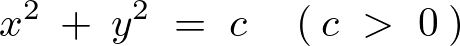
これを![]() で微分するとどうなるでしょうか?
で微分するとどうなるでしょうか?
実際にやってみると、
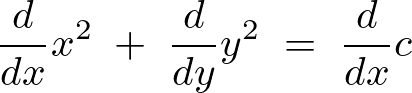
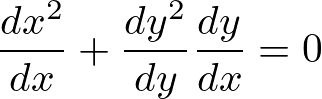
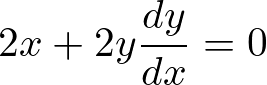
求められた式を整理すると以下のような方程式が求まります。
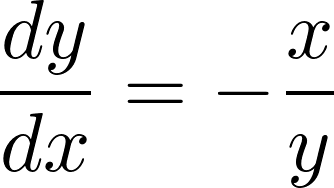
これは円の接線方向の傾きを意味しています。
【例3】力学への応用
一様な重力場中における質点の力学的エネルギー
全微分の式を使って、力学的エネルギー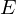 が時間によらず一定、
が時間によらず一定、
つまり、
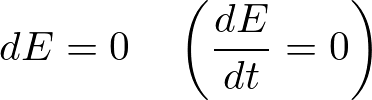
であることの証明をします。
ちなみに時間で微分する場合は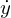 などという書き方をします。
などという書き方をします。
意味的には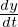 と全く同じになります。
と全く同じになります。
呼び方はドットとといいますので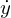 はワイのワンドットなどといったりします。
はワイのワンドットなどといったりします。
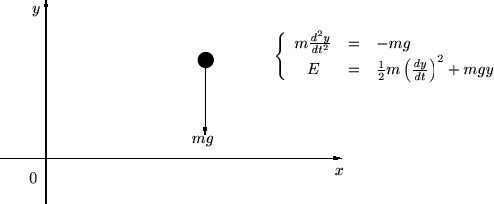
力学的エネルギー![]() の式には変数が
の式には変数が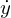 と
と![]() の2つになっているのでと表せます。
の2つになっているのでと表せます。
これに対して全微分の式を適用させれば、
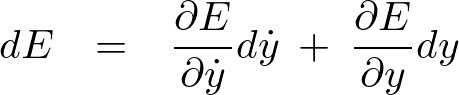
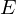 の式に対してそれぞれ
の式に対してそれぞれ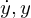 で偏微分します。
で偏微分します。

先ほどの全微分の式に対してこの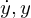 の偏微分の式を代入します。
の偏微分の式を代入します。
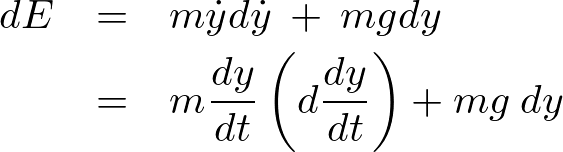
この式をスカラー倍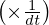 します。
します。
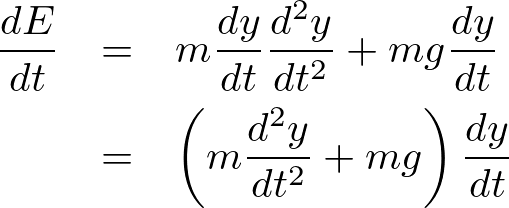
ここで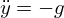 より
より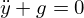 。
。
これにより、
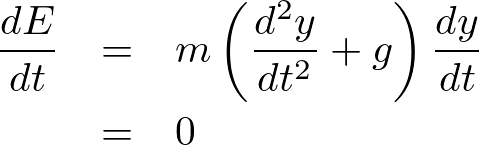
よって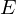 は時間によらず一定であることがわかりました。
は時間によらず一定であることがわかりました。
上記にあげたコンテンツが微分方程式の簡単な参考程度のものです。
◆このサイトの趣旨
このサイトは管理人が備忘録的要素も兼ねながら外環境にコンテンツを順次アップロードしているサイトになります。 更新頻度は数週間から数か月に1コンテンツぐらいになるかと思いますが現在、管理人が多忙のためそれ以上になっております。
その辺のところを何卒ご了承くださいますようよろしくお願申し上げます。
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、

この連立微分方程式に関して具体的に解いていきます。
まず の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。