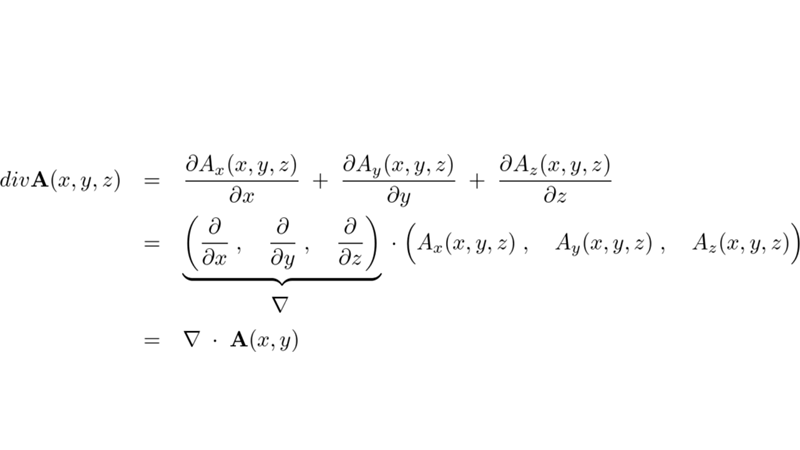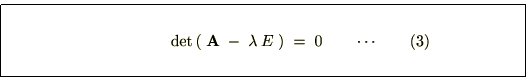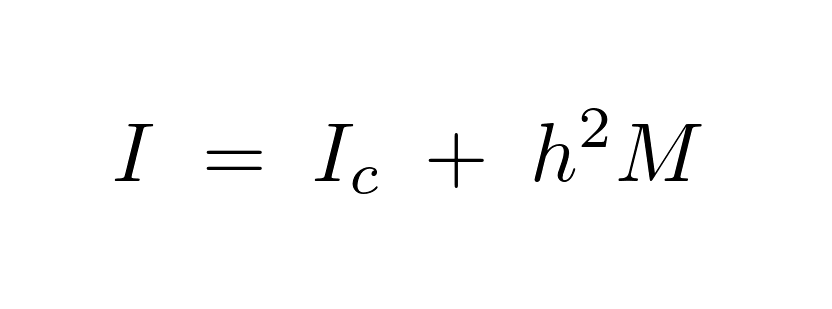モーメント母関数とは
ある確率変数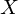 に対して、
に対して、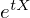 の期待値を
の期待値を のモーメント母関数、または積率母関数などといったりします。
のモーメント母関数、または積率母関数などといったりします。
ガウス関数のフーリエ変換のコンテンツでやったようにこのモーメント母関数というものも、ある現象では見通しが悪かったものがこのモーメント母関数というのを利用して別の角度からとらえてみると見通しが良くなったりすることがあります。フーリエ変換の確立関数版みたいな感じです。
次のような式で表現されます。
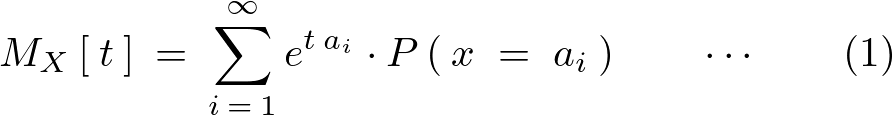
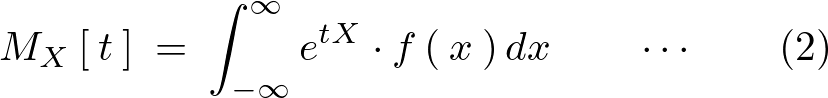
上記式の(1)を離散型、(2)のほうを連続型などというそうです。
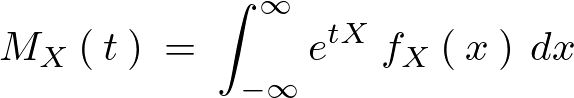
モーメント母関数の微分
1階微分
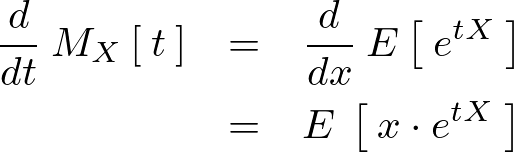
ここで![]() を代入すると、
を代入すると、
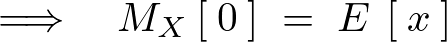
2階微分
2階微分では、
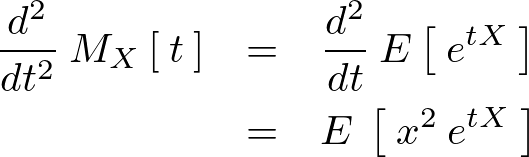
同様にして![]() を代入すると、
を代入すると、
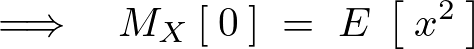
分布関数のモーメント母関数計算
正規分布関数
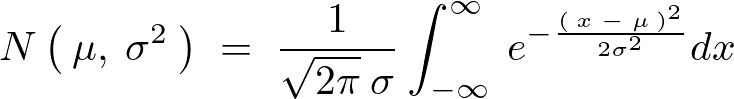
上記式はこのサイトで何回か出てきているお馴染みの関数“正規分布関数”と呼ばれるもので、式中の![]() は平均、
は平均、![]() は分散を表しています。
は分散を表しています。
この式をモーメント母関数にしたがって表記すると次のような式になります。
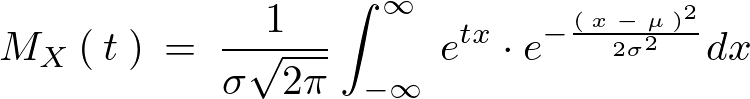
正規分布関数のモーメント母関数を求めるために上記の式を実際に計算(積分)していきます。
まず見やすいようにするために上記式中の![]() の部分だけを抜き出して計算していきます。
の部分だけを抜き出して計算していきます。
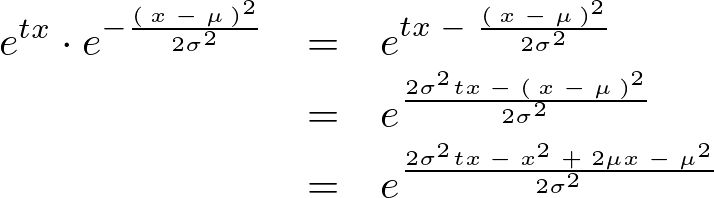
ここでさらに見やすいように![]() の乗数部分を抜き出してそこの計算を行います。
の乗数部分を抜き出してそこの計算を行います。
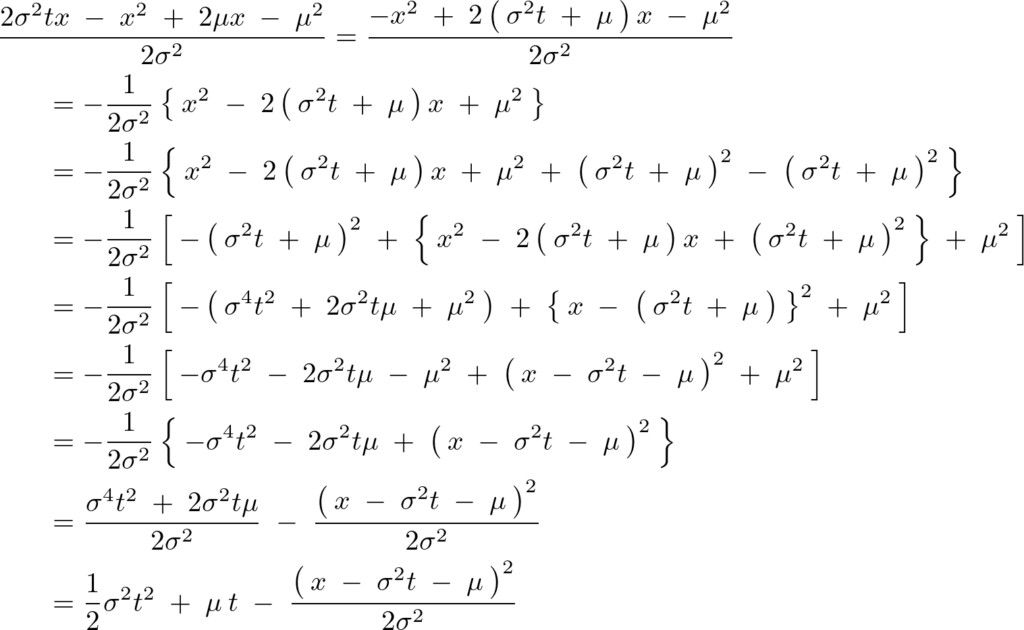
よって正規分布関数のモーメント母関数の式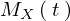 は次のような式に変形できます。
は次のような式に変形できます。
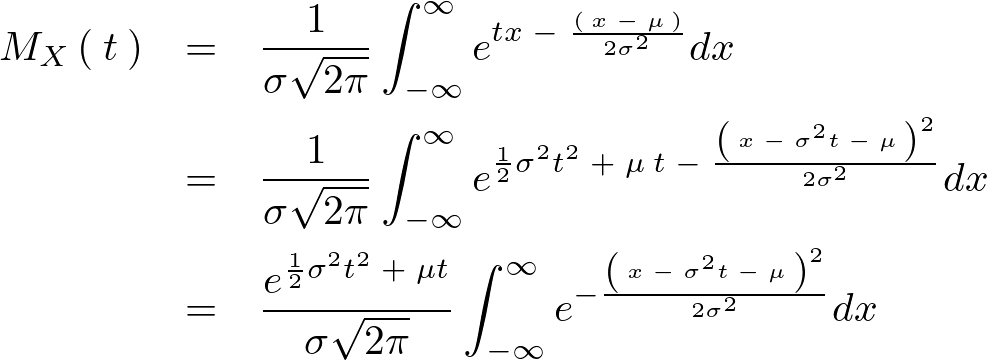
ここで次のように置換します。
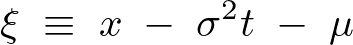
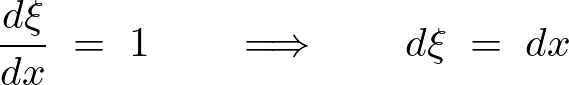
これを代入すれば、
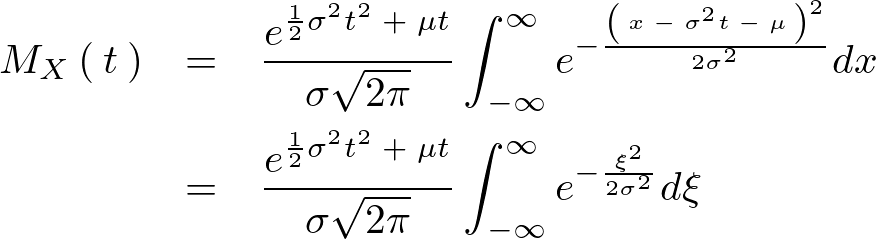
さらにまた![]() の乗数部分を
の乗数部分を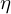 とおいて置換していきます。
とおいて置換していきます。
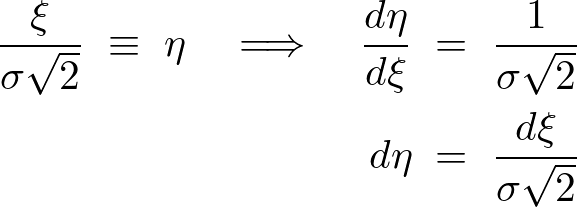
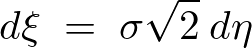
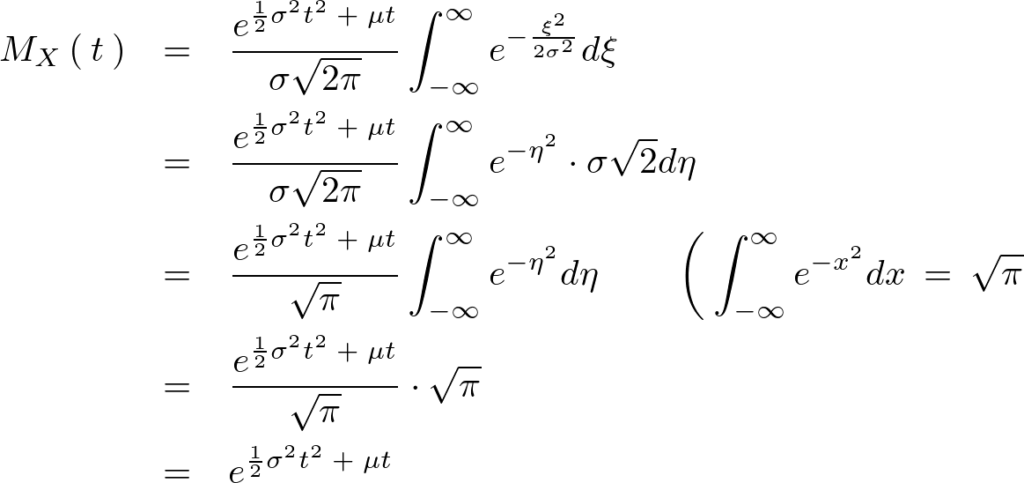
よって正規分布関数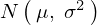 の求められるモーメント母関数は次のようになります。
の求められるモーメント母関数は次のようになります。
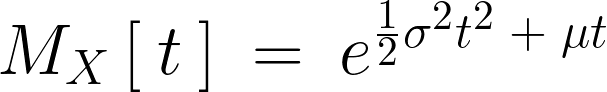
-
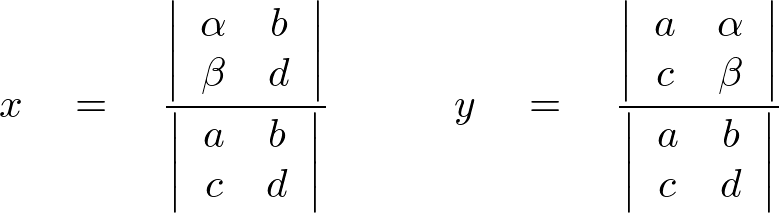
行列式による連立方程式の解法
カテゴリー
-
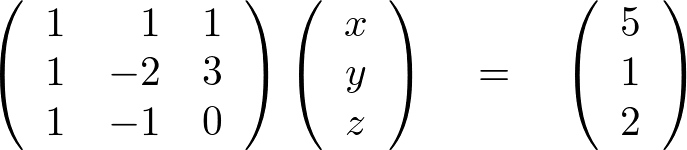
行列式を使った連立方程式の解き方
カテゴリー
-

剛体の運動
カテゴリー
-

1変数関数の積分
カテゴリー
-

2重積分
カテゴリー
-
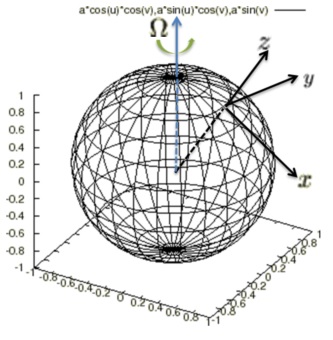
三次元ベクトル場および発散についての補足
カテゴリー : 三次元ベクトル場、発散についての補足三次元ベクトル場の発散(ダイバージェンス)に関して、ナブラとベクトル場の内積との関係について考察してみましょう…
-
-
-
-
-
-
-
-
-