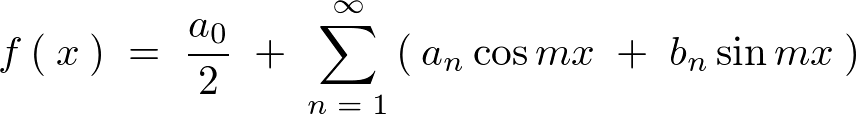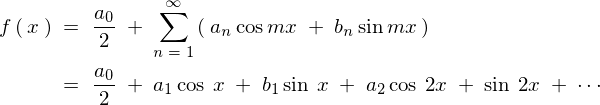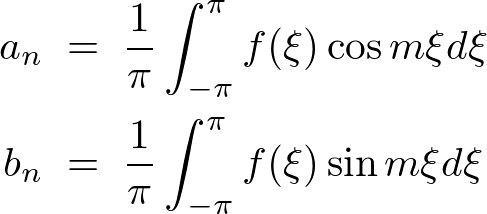���A�����I�ł͂Ȃ������������Ƃ��܂��B
���̂Ƃ��A
| ���� |  |
|---|
�ƍl���邱�Ƃ��o���邩�Ǝv���܂��B
�����������Ƃ��A�t�[���G�����̓t�[���G�ϕ��Ƃ�����̂ɂȂ�܂��B
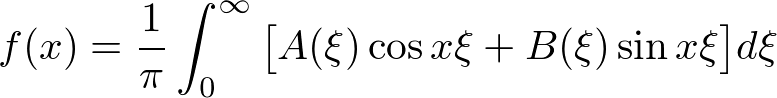
��L����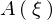 �A
�A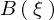 �͈ȉ��̂悤�ɂȂ�܂��B
�͈ȉ��̂悤�ɂȂ�܂��B
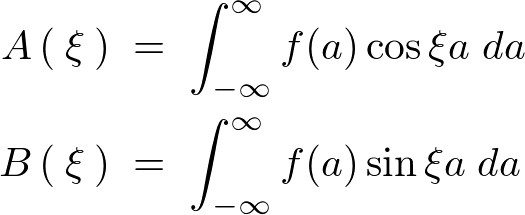
���ۂɑ�����Ă݂�ƁA
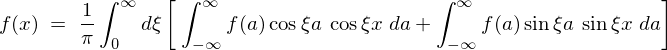
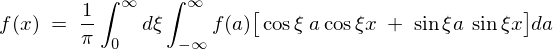
�����ŎO�p���̊W��
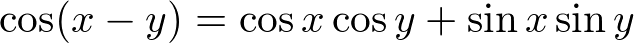
���A
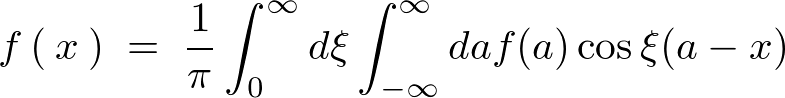
������t�[���G�ϕ������ȂǂƂ������肵�܂��B
�M�`���������������ۂɂ��̏�L�̌����ɗႦ�Ώ搔�ɕϐ�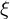 �̂���
�̂���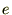 ���ꏏ�ɂ���ꍇ�̌v�Z���K�v�ɂȂ�܂��B
���ꏏ�ɂ���ꍇ�̌v�Z���K�v�ɂȂ�܂��B
�ꉞ�����������ꍇ�̐ϕ�����������悤�Ȃ̂ł����A���ꂾ�Ɖ��p�������Ȃ��̂ŗ��ł��̉�@�����������Ǝv���܂��B
���������̐ϕ��͓������o���܂ł����X���ł��B



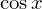 ��
�� �̃O���t������킩��悤�ɁA
�̃O���t������킩��悤�ɁA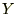 ���𒆐S�ɍl����Ƃ��ꂼ�ꂪ���E�Ώ̂Ɣ�Ώ̂ɕ�����Ă��܂��B
���𒆐S�ɍl����Ƃ��ꂼ�ꂪ���E�Ώ̂Ɣ�Ώ̂ɕ�����Ă��܂��B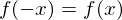 �Ȃ̂ŋ����A
�Ȃ̂ŋ����A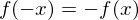 �Ȃ̂Ŋ���ł���Ƃ����܂��B
�Ȃ̂Ŋ���ł���Ƃ����܂��B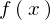 �������A�܂��͊���̂ǂ��炩����ł������Ȃ���̃t�[���G����
�������A�܂��͊���̂ǂ��炩����ł������Ȃ���̃t�[���G����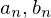 �̂��ꂼ��̂ǂ��炩�����
�̂��ꂼ��̂ǂ��炩�����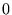 �ɂȂ�܂��B
�ɂȂ�܂��B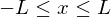 �Ɋg��������
�Ɋg��������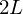 �̎������ɂ���ƁA���̎������̃t�[���G�����W�J�͎��̂悤�ɂȂ�܂��B
�̎������ɂ���ƁA���̎������̃t�[���G�����W�J�͎��̂悤�ɂȂ�܂��B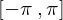 �͎��̂悤�a�̋L����p���ċ����ɓW�J���邱�Ƃ��\�ł���Ƃ��܂��B
�͎��̂悤�a�̋L����p���ċ����ɓW�J���邱�Ƃ��\�ł���Ƃ��܂��B