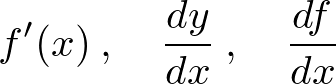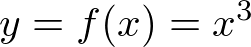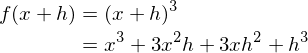������Ԃɂ�����ϕ��ő��ɃK�E�X�ϕ��ƌ�������̂�����܂��B
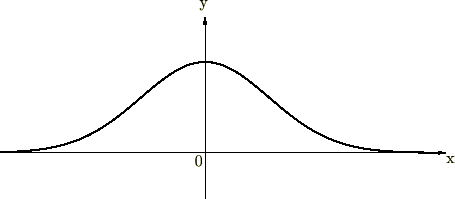
���}�͎w����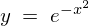 ��`�悵�����̂ł��B
��`�悵�����̂ł��B
���̊���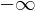 ����
����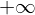 �͈̔͂ɂ����Đϕ������s����ǂ��Ȃ�ł��傤���H
�͈̔͂ɂ����Đϕ������s����ǂ��Ȃ�ł��傤���H
���̓�����P�������ɏ����Ǝ��̂悤�ɂȂ�܂��B
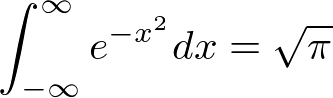
�͂��߂Č������͑����������Ǝv���܂��������������ʂ��m���ɂ܂���ʂ��Ă��܂��B
���̂��߂��̐ϕ��̂��Ƃ��A�K�E�X�̃C���`�L�ϕ��ȂǂƂ������肷����̂����܂ɂ��܂��B
�����ł͑�w�Ŏ��Ƃ��̎����̍u�`�m�[�g���Q�l�ɐ����������Ƃ������܂��B



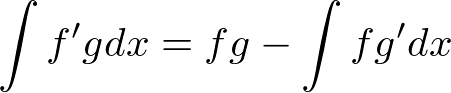
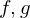 �̉E��ɂ��Ă���
�̉E��ɂ��Ă��� �Ƃ����L���͈����������Ƃ����Ӗ��ł��B
�Ƃ����L���͈����������Ƃ����Ӗ��ł��B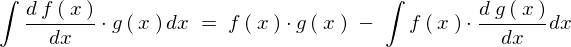
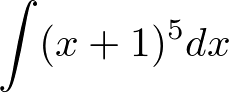
 �ɒ��ڂ��Ă��������
�ɒ��ڂ��Ă��������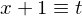 �Ƃ����܂��傤�B
�Ƃ����܂��傤�B ��������ƁA
��������ƁA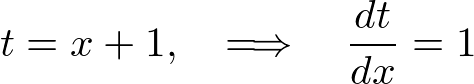
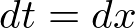
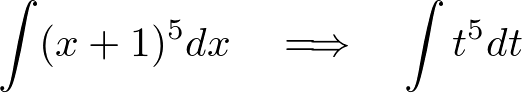
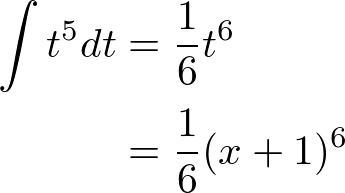
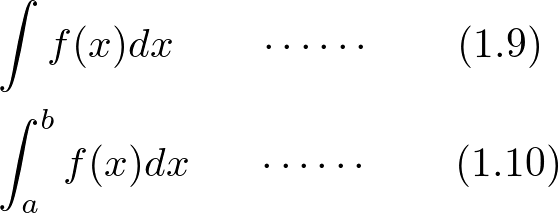
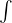 �h�̓C���e�O�����Ƃ����ϕ����̂��̂��Ӗ����܂��B
�h�̓C���e�O�����Ƃ����ϕ����̂��̂��Ӗ����܂��B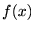 ����ϕ����ł���A
����ϕ����ł���A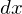 �͂��̏ꍇ
�͂��̏ꍇ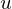 �Ƃ������L�����g���Ă��\���܂���B
�Ƃ������L�����g���Ă��\���܂���B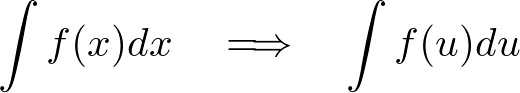
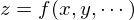 �@�|�@���ׂĂ̕ϐ�������ʓ������Ƃ�������
�@�|�@���ׂĂ̕ϐ�������ʓ������Ƃ�������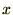 �������
�������
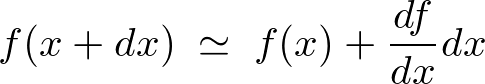
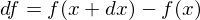 �Ə����Ȃ�A
�Ə����Ȃ�A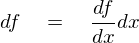
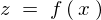 �̑S�����Ƃ����܂��B
�̑S�����Ƃ����܂��B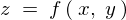 ���l���Ă݂܂��傤�B
���l���Ă݂܂��傤�B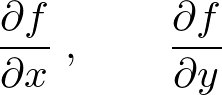
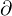 �h�͕���ɂ���ϐ��ŕΔ�������Ƃ����Ӗ��̋L���ł��B
�h�͕���ɂ���ϐ��ŕΔ�������Ƃ����Ӗ��̋L���ł��B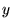 �̂��ꂼ��ɕΔ������s���Ă݂܂��傤�B
�̂��ꂼ��ɕΔ������s���Ă݂܂��傤�B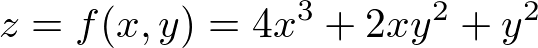
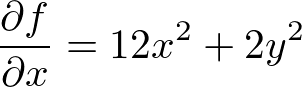
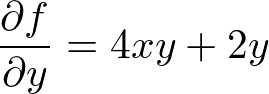
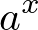
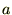 ���萔��
���萔��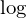 ���Ƃ邱�Ƃ���l����̂ŁA�܂����̎���
���Ƃ邱�Ƃ���l����̂ŁA�܂����̎��� �Ƃ����܂��B
�Ƃ����܂��B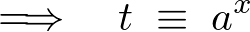
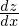 �ł����A
�ł����A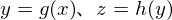 �Ƃ��܂��B
�Ƃ��܂��B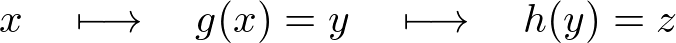
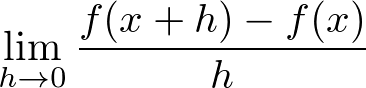
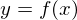 �̓����ƌĂт܂��B
�̓����ƌĂт܂��B