���`�d��A���f���i�쐬�ҏW���j
���j���̃R���e���c�͌��ݍ쐬�ҏW���ɂȂ�܂��B
�{���͎��Ɖ��M�Ő������v�Z���ؖ��������̂�LaTeX�R�[�h�ɂ���texclip�l�̂Ƃ���ŏo�͂�����HTML�ɍڂ��Ă��܂������A����͒��ڐ����摜���o�͂����Ă��̏�Ő����ߒ����m�F���ăA�b�v���[�h���Ă��܂��B���̂��߂��Ȃ�璷�ȓ��e�ɂȂ��Ă���̂Ŋ�{�I�Ɍv�Z�ߒ��̂قƂ�ǖ��ʂȕ����ł��B�Ȃ̂ł��������̂͂قږ������Ă��������B�������������́u�f�[�^�̌����v�Ȃǂ̃G���g���[���i���Ԃ�j�쐬���Ăق��Ɉڂ��܂��B
�Ȃ̂ŁA���̂ւ�̂Ƃ��뉽����낵�����Ȃ������ܽ���<�M�́L>
�ȉ��{����
�P��A���͂̐����ϐ����ЂƂȂ̂ɑ��Đ����ϐ���2�ȏ゠��f�[�^���f�����l���A����ʂ����̂悤�ȑ������̃x�N�g�����z�A
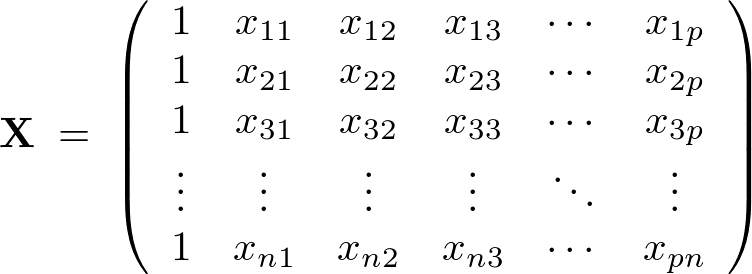
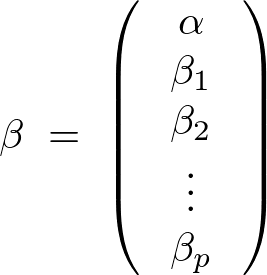
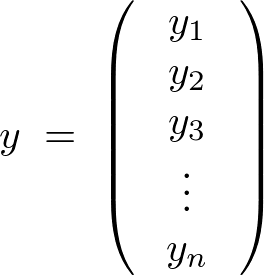
�ł���悤�Ȑ����ϐ��A�ړI�ϐ��A��A�W������Ȃ�f�[�^�\�����l�����Ď��̂悤�ȃf�[�^���f�����l����B
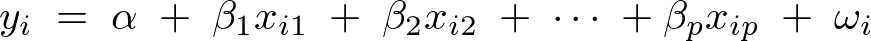
��L���̉�A�����ɂ�����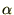 �͐ؕЂ��Ӗ����A
�͐ؕЂ��Ӗ����A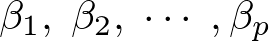 �͉�A�W���ɂȂ�B
�͉�A�W���ɂȂ�B
�f�[�^�̕\��
���ς̕\����
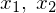 �̕��ς̕\����
�̕��ς̕\����
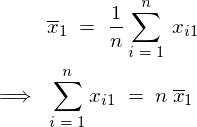
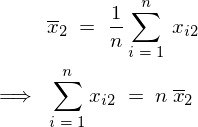
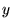 �̕��ς̕\����
�̕��ς̕\����
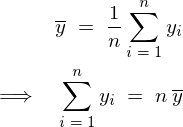
�s���U
���ꂼ��̕s�Ε��U�����̂悤�ɕ\������B
�s���U
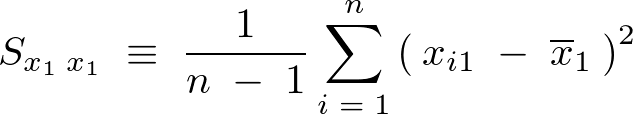
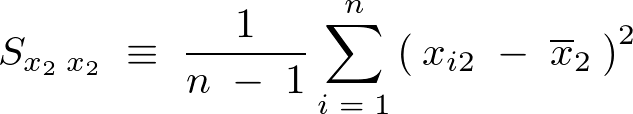
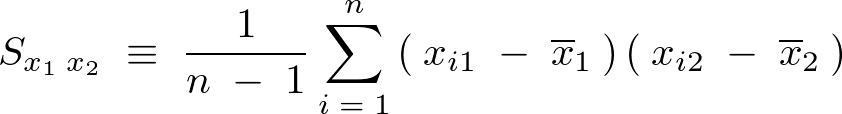
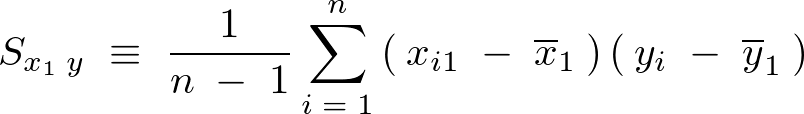
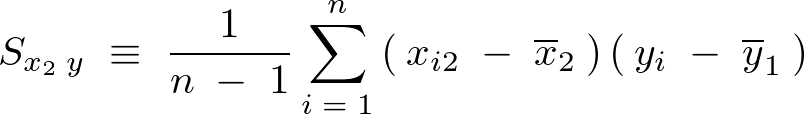
�c�������a�Ƃ����l��
�ؕЂł���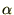 �ƌX��
�ƌX��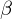 �̉�A������\��������
�̉�A������\��������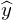 �̎��Ǝ��ۂ̊ϑ��l
�̎��Ǝ��ۂ̊ϑ��l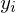 �Ƃ̍����c���Ƃ��Ď��̂悤�ɍl���邱�Ƃɂ���B
�Ƃ̍����c���Ƃ��Ď��̂悤�ɍl���邱�Ƃɂ���B
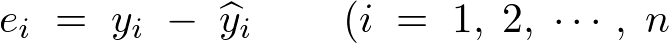
�n�b�g�͗\���l�␄��l��\���ۂɗp������(�t�B�b�V���[���ʂ̃R���e���c�Q��)�B
�c�������a
�����Ă����̂��̊ϑ��l�ɑ���c���̓��a�`�c�������a�����̂悤�ɕ\�����Ƃɂ���B
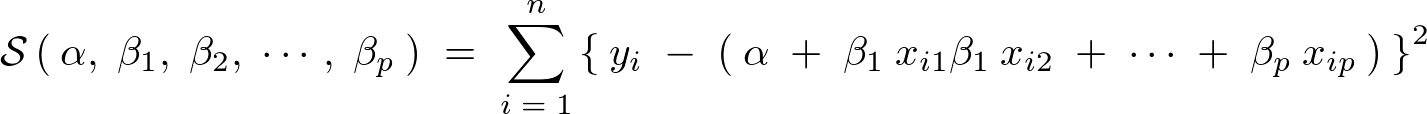
��L���ɂ����Ď��ۂ̊ϑ��l�̍����Ȃ������ꍇ�A�܂�O�ł�����̎c�������a��0�ɂȂ�ƍl����(���O�����W������搔�@�Ƃ������Ƃ炵��)�B
���̎c�������a���\�Ȍ���O�i�ŏ��j�ɂȂ�悤�ȉ�A�W���Q�����߂���@���ŏ�2��@�iLSM�Fleast squares method�j�ƌĂԂƂ̂��ƁB
��L���ɂ����Ă��ꂼ��̃p�����[�^�ł��郿�A���ŕΔ�����������0�ƒu�������̂��̗p���Ă����Đ��K���������Ă����B
���K�������̓��o
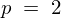 �Ƃ����ꍇ
�Ƃ����ꍇ
�����ł͊ȒP�̂��߂ɂo��2�ƒu�����ꍇ��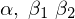 ���l����B
���l����B
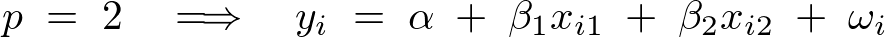
��L���ɂ�����덷�̕����a�͈ȉ��̂悤�ɕ\������B
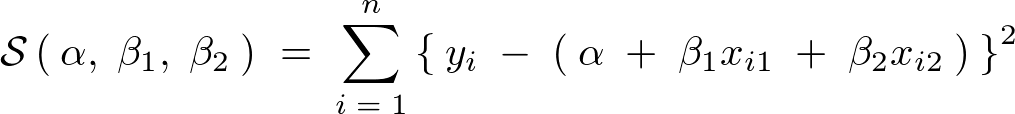
���̏�L���ɂ����č��ӂ́A
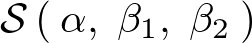
����A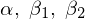 �Ɋւ��čŏ������邱�Ƃ��l����悤�ɂ���B
�Ɋւ��čŏ������邱�Ƃ��l����悤�ɂ���B
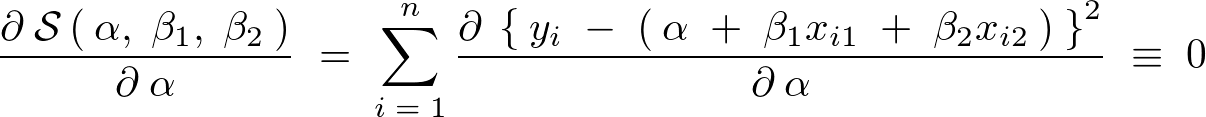
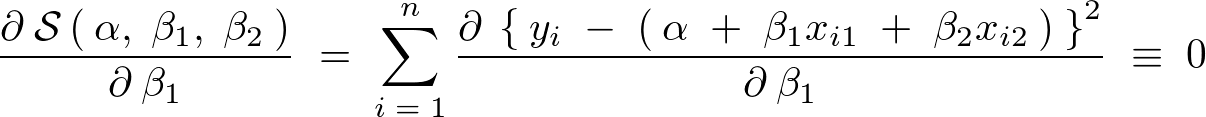
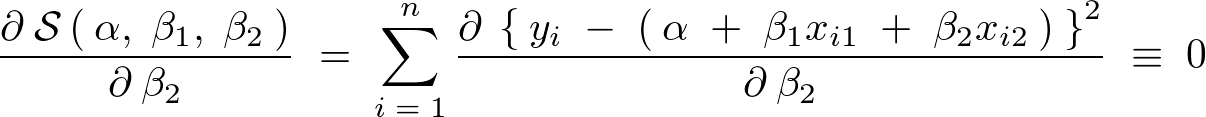
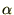 �ɂ��Δ���
�ɂ��Δ���
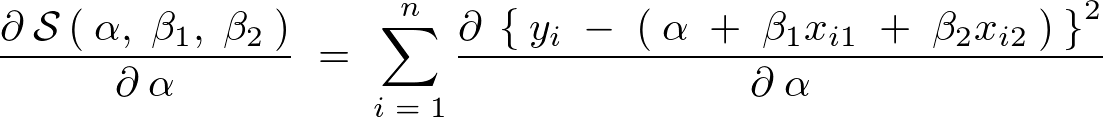
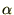 �ŕΔ������Ă����B
�ŕΔ������Ă����B
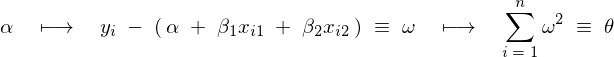
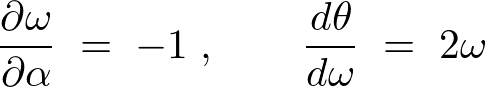
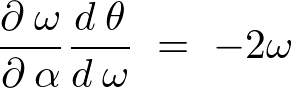
���̌��ʂ��A
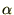 �ɂ��Δ����̌��ʂ́A
�ɂ��Δ����̌��ʂ́A
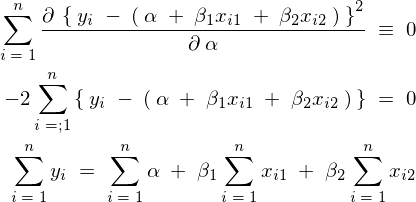
���A���������A
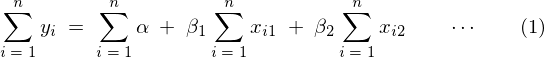
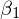 �̕Δ����ɂ���2�������̓��o
�̕Δ����ɂ���2�������̓��o
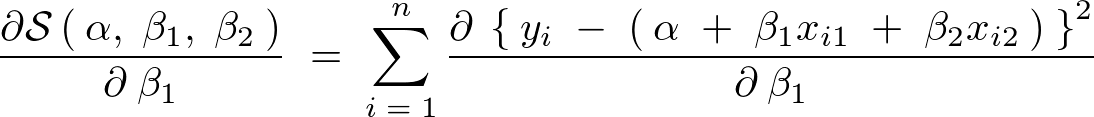
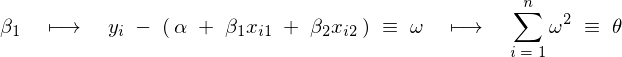
���A
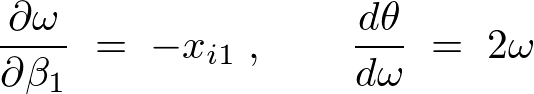
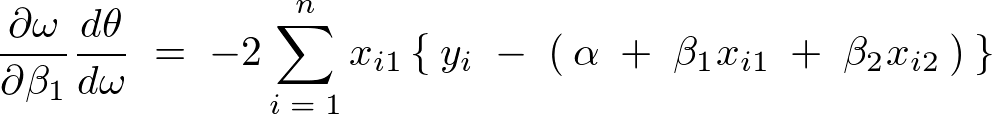
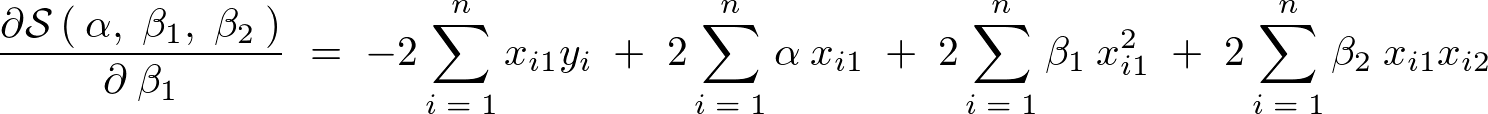
�Əo�邪�A���̂悤�ɁA
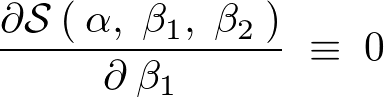
�Ȃ̂ŁA
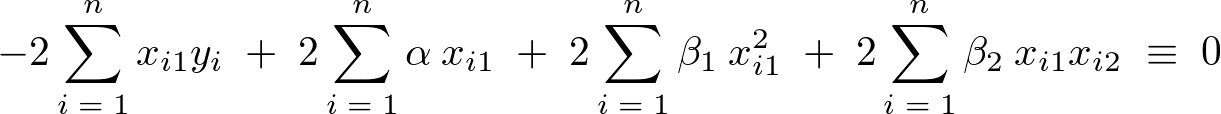
��������Ǝ��̂悤��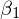 �̑�2���K�����������܂�B
�̑�2���K�����������܂�B
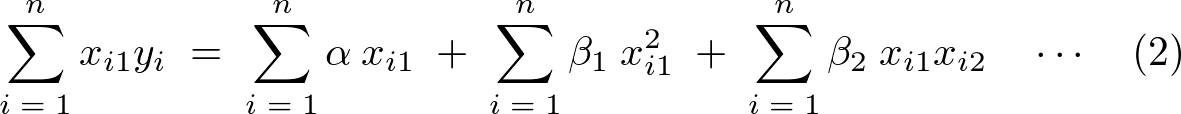
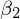 �̕Δ����ɂ���3���K�������̓��o
�̕Δ����ɂ���3���K�������̓��o
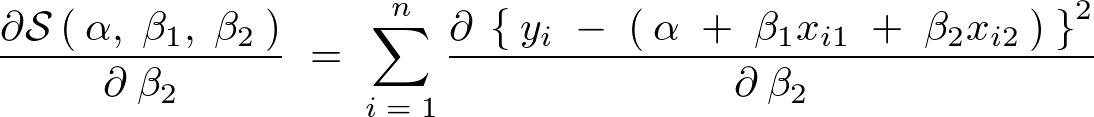
���Q�̕Δ����B
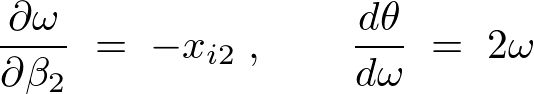
���A
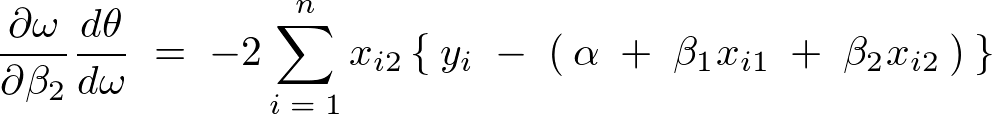
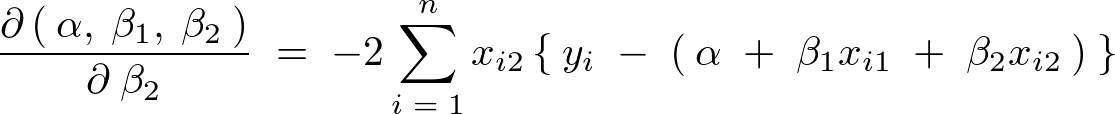
�����悤�ɍŏ��ƂȂ�悤�Ɏ��̂悤�ɒu���A
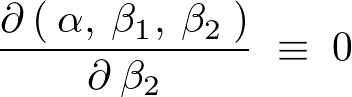
�ƂȂ�̂ł��̂悤��
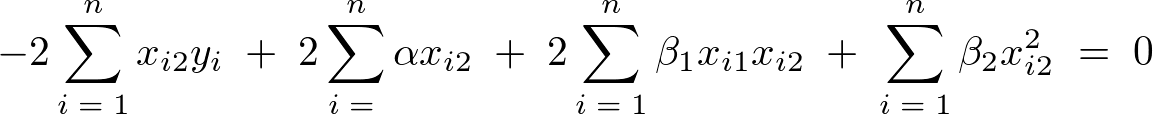
��3���K�����������܂�B
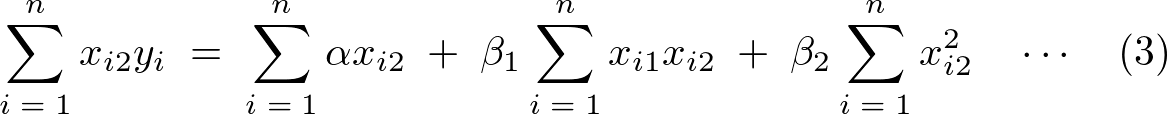
�����ɂ���Ĉȉ��̂悤��3�̕����������܂�B
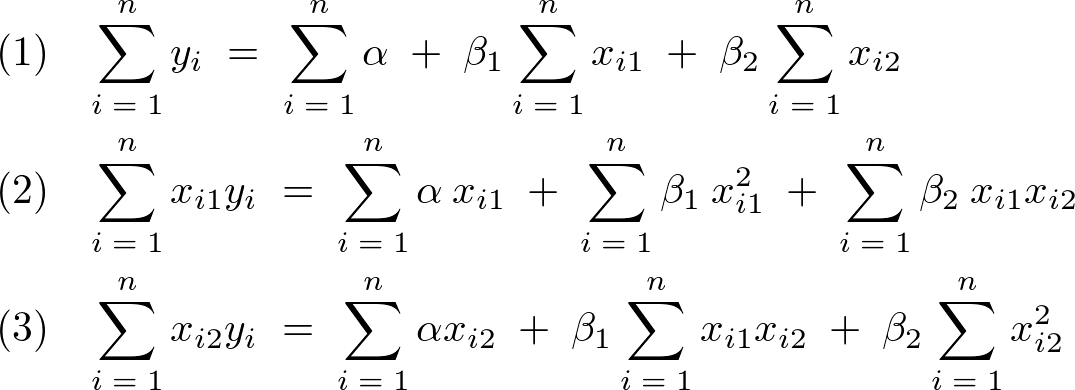
�i�P�j���̕ό`
�����ŕ��ς̎��A
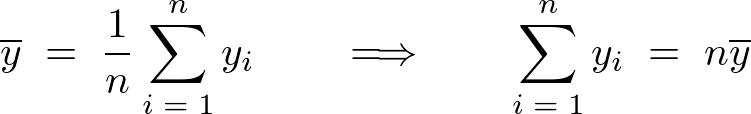
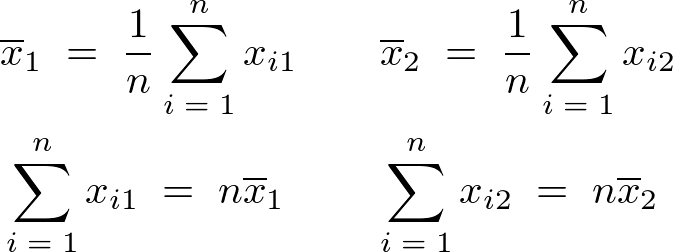
�̎��Ə�L�i�P�j�̎��A
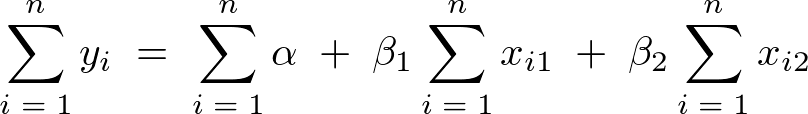
���A
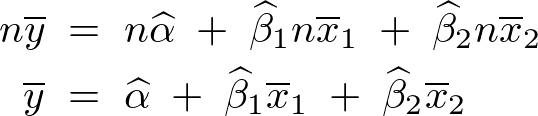
���ӉE�ӂ��ړ�������܂��ŏ���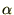 �Ɋւ��Ď��̂悤�Ȏ������܂�B
�Ɋւ��Ď��̂悤�Ȏ������܂�B
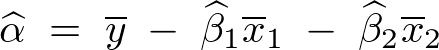
�i�Q�j���̕ό`
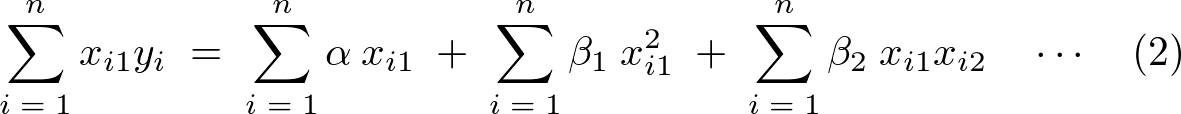
����قNj��܂���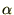 �̎��������Čv�Z���Ă����B
�̎��������Čv�Z���Ă����B
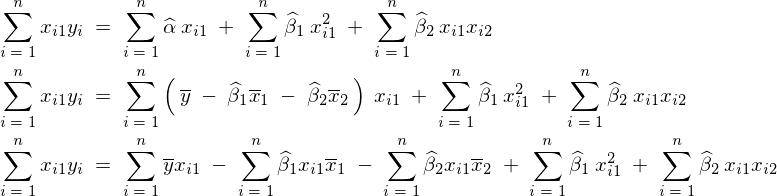
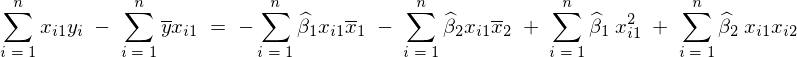
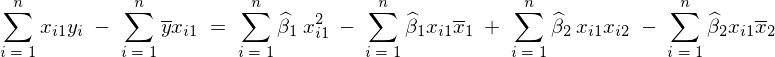
���̌��ʂɂ�莟�̂悤�ȑ�2���K�����������܂�B
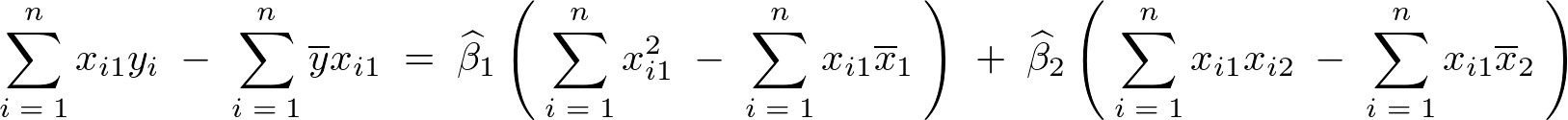
(3)���̕ό`
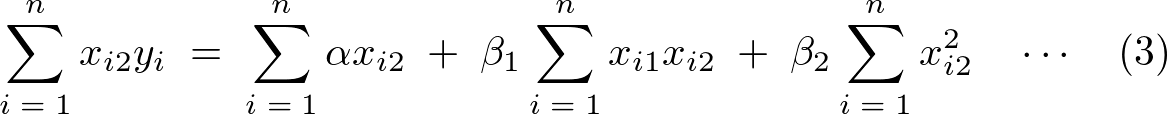
���l��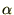 �Ɋւ��Ă̎�����L��3�������ɑ�����Ă����B
�Ɋւ��Ă̎�����L��3�������ɑ�����Ă����B
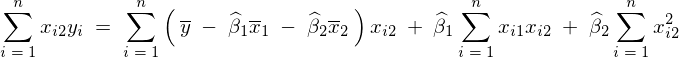
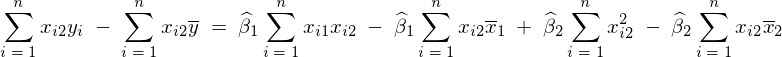
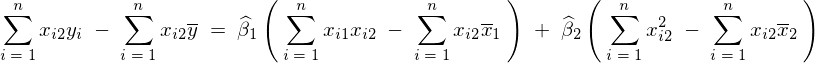
�ƂȂ�̂ő�3�������Ɋւ��Ď��̂悤�ɋ��܂�B
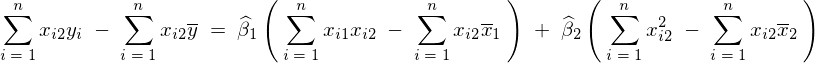
���ʓI�Ɏ��̂悤��3�̎������܂�B
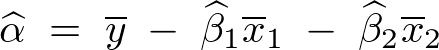
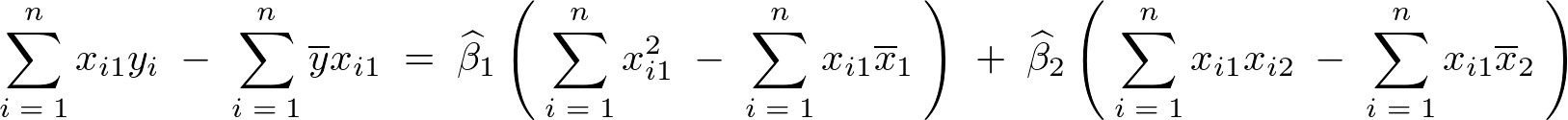
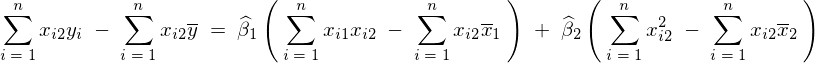
�s�Ε��U���̕ό`
�����ŕs�Ε��U���Ȃǂ̃f�[�^�\���Ɋւ����A�̎��̕ό`���l�@����B
�ЂƂ܂����ς͎��̂悤�ɕ\������B
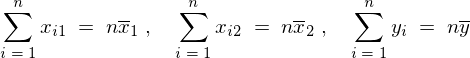
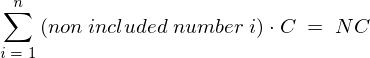
��L����p���ĕs�Ε��U��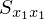 ���ȉ��̂悤�ɕό`���Ă����B
���ȉ��̂悤�ɕό`���Ă����B
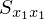 ���̕ό`
���̕ό`
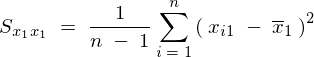
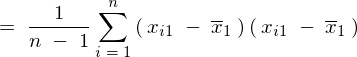
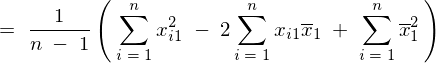
�����Ő�قǕό`�������ς̎��������Ă����B
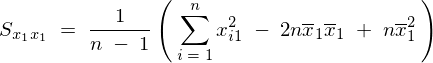
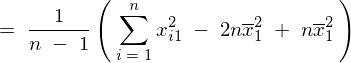
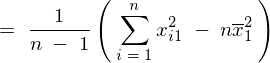
����Ă܂��ŏ��Ɏ��̂悤�Ȏ������߂���B
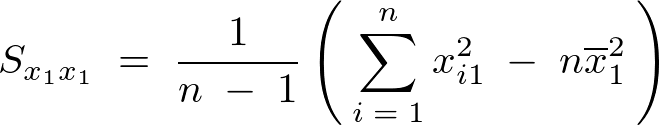
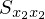 ���̕ό`
���̕ό`
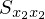 �̎��̕ό`�����̂悤�ɓ��l�ɍs���Ă����B
�̎��̕ό`�����̂悤�ɓ��l�ɍs���Ă����B
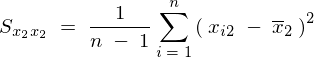
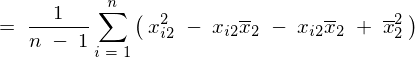
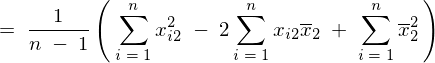
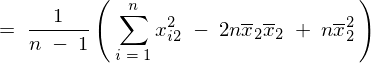
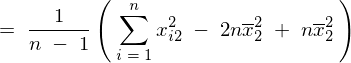
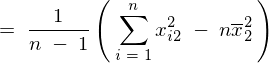
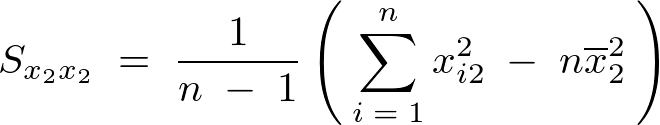
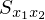 ���̕ό`
���̕ό`
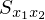 �̎��ό`�ߒ�
�̎��ό`�ߒ�
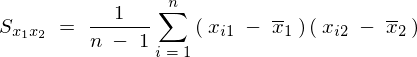
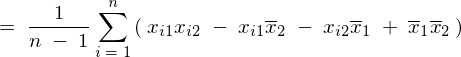
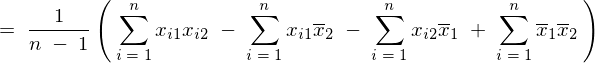
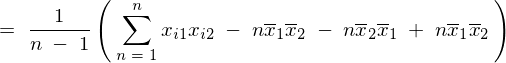
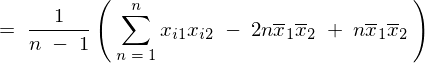
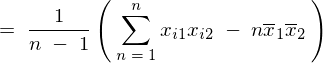
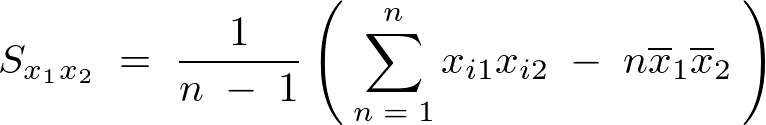
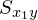 ���̕ό`
���̕ό`
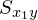 ���̕ό`�ߒ�
���̕ό`�ߒ�
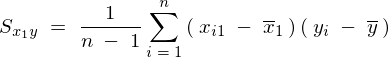
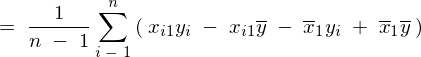
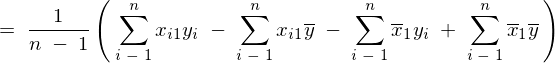
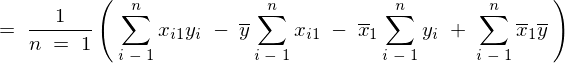
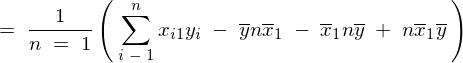
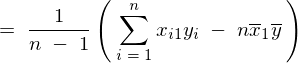
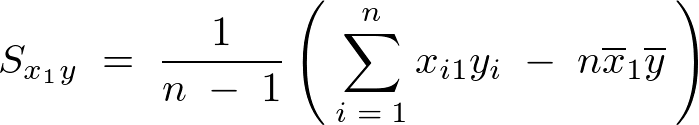
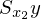 ���̕ό`
���̕ό`
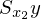 ���̕ό`�ߒ�
���̕ό`�ߒ�
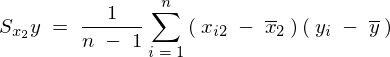
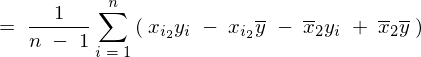
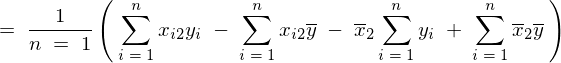
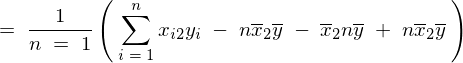
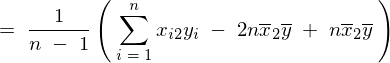
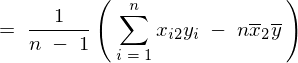
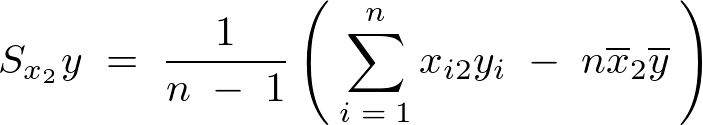
�ƂȂ�̂ňȏ�A��L5�̕s�Ε��U���͂܂Ƃ߂�ƈȉ��̂悤�ɕ\���ł��邱�ƂɂȂ�B
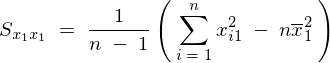
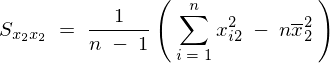
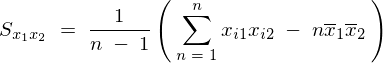
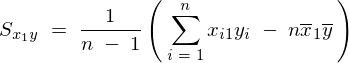
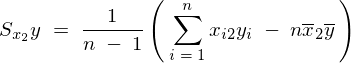
�����Ă͂܂�ƁA��قNj��܂���3���̐��K�������̂����̎���2�̐��K�������A
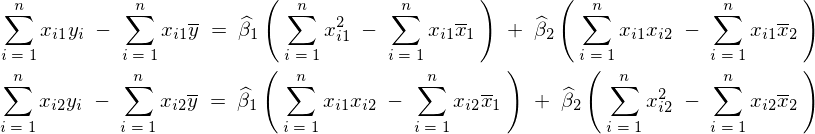
�́A�܂��ŏ��ɐ�قǂ̕��ς̎��Ă͂߂�Ύ��̂悤�ɕ\���ł��邱�ƂɂȂ�B
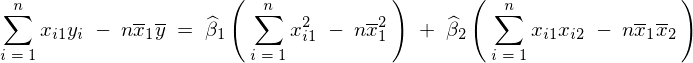
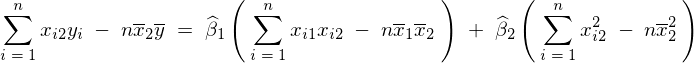
�s���U�����A
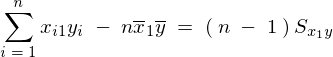
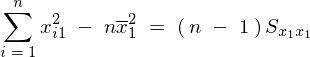
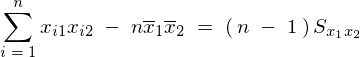
�������2�������ɑ������A
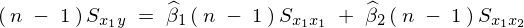
�܂����̂悤�ȊW�������܂�B
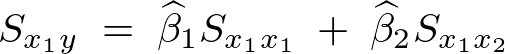
���l�ɑ�3�������A
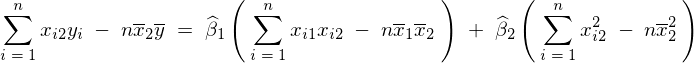
�Ɋւ��Ă��A
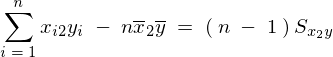
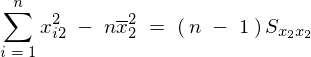
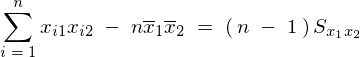
���g���A
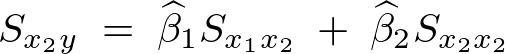
�܂Ƃ߂�Έȉ��̂悤�ȕs�Ε��U���Ɖ�A�W��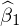 �A
�A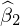 �̊W�������܂�B
�̊W�������܂�B
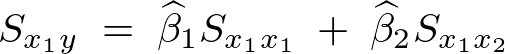
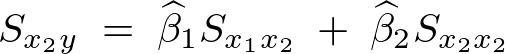
�����̌W���Ɋւ���A���������ɂȂ��Ă���̂ł���������Ă����B
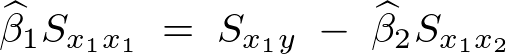
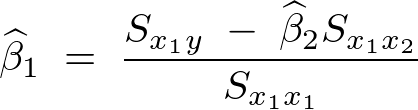
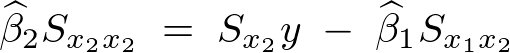
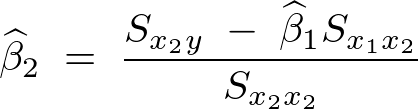
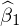 �̓��o
�̓��o
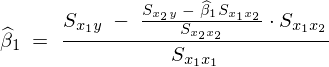
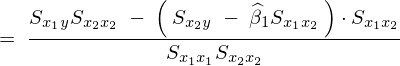
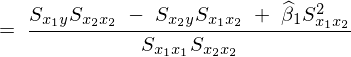
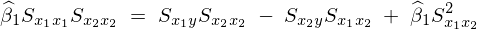
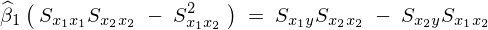
���Ή�A�W��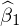 �͈ȉ��̂悤�ɂȂ�B
�͈ȉ��̂悤�ɂȂ�B
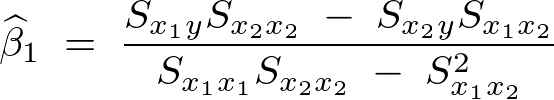
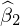 �̓��o
�̓��o
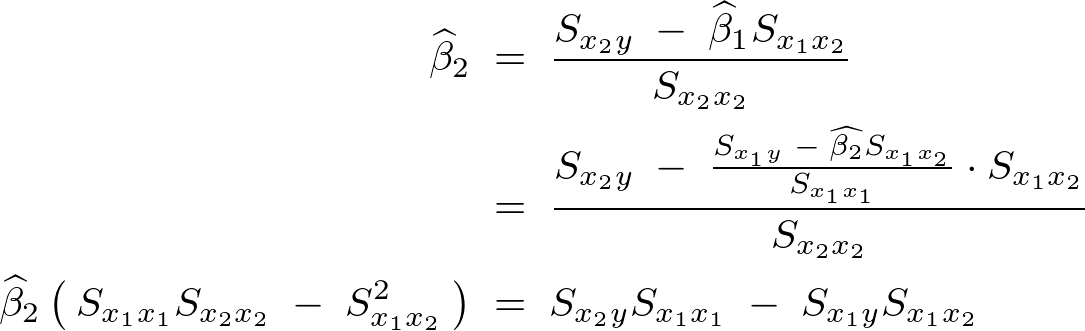
���A
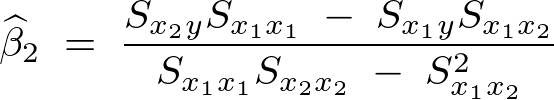
���ȉ��̂悤�ɋ��܂�܂��B
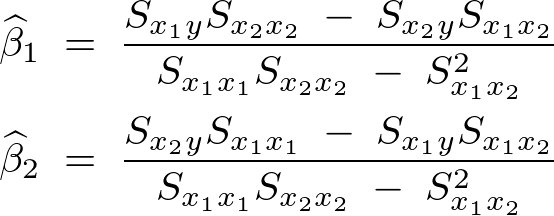
�c�������a�ƑS�ϓ����̎��ό`
��قǂ��O�̂ق��Ŏ��������ēx�\�L����ƈȉ��A
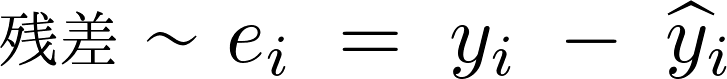
�܂��������a�A�܂��͑S�ϓ��͎��̂悤�ɍl���Ă�B
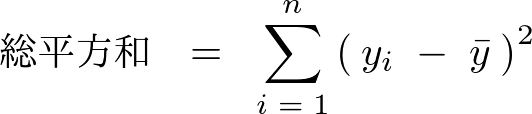
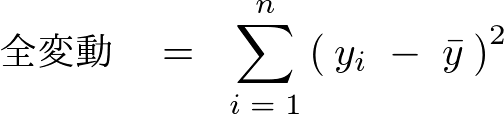
�Ȃ̂ŁA
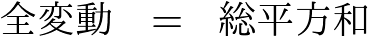
�����Ŏc���������̂悤�ɂ����Ďc�������a�Ƃ���B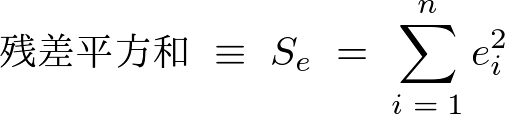
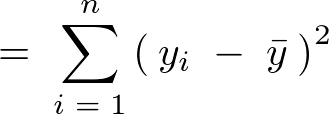
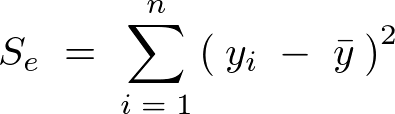
�܂�����Ɏc�������ȉ��̂悤�ɁA
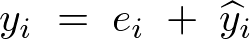
�Ƃ����āA�S�ϓ��i�������a�j�̎��ɑ������B
�S�ϓ��̎����A
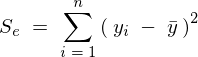
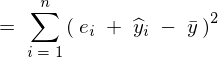
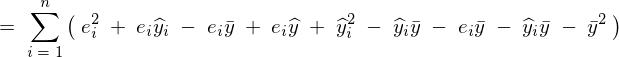
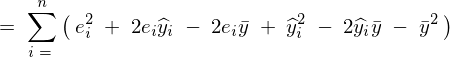
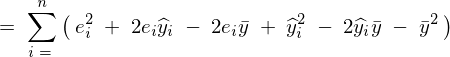
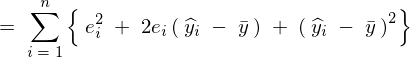
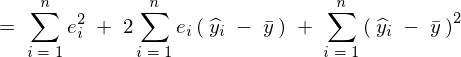
���Ɏc���̑��a���l����B
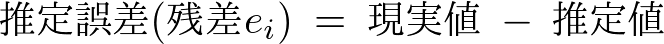
�܂�����l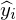 �́A
�́A
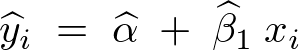
���A
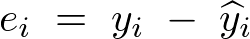

���̎c��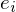 �̑��a
�̑��a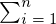 ���l����B
���l����B
�܂�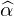 �͈ȉ��A
�͈ȉ��A
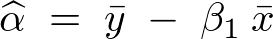
�ɂ��c���̘a�͎��̂悤�Ɍ��ʂ��o����B
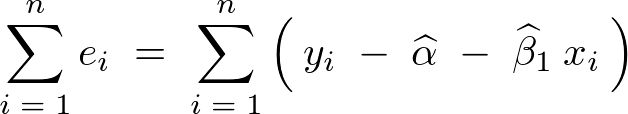
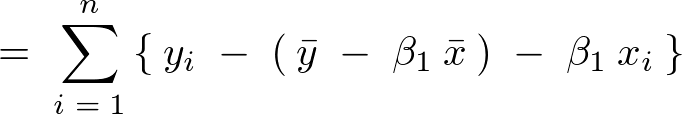
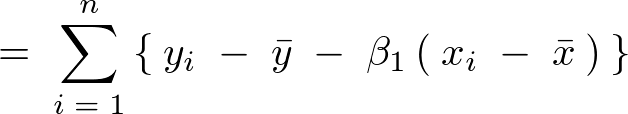
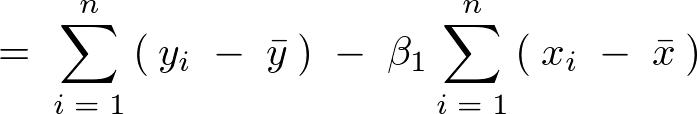
�ƂȂ邪�E�ӑ�1���A��2���̑��a��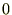 �ɂȂ�̂ňȉ��̂悤�ɂȂ�B
�ɂȂ�̂ňȉ��̂悤�ɂȂ�B
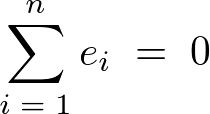
�⑫�j���ۂ�10���炢�̒l�����o���đ��a�ƕ��ς��o���ĉ��M�Ōv�Z���Ċm���߂�����B
�ƂȂ�̂Ő�قǓ����ꂽ�S�ϓ��̎��A
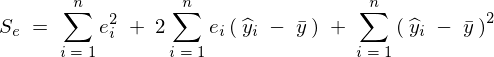
�Ɋւ��ĉE�ӂ̑�2���̓L�����Z������Č��ʓI�Ɉȉ��̂悤�ȕ����������܂�B
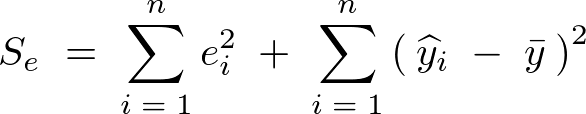
�܂��r������























