�t�[���G�ϊ��Ƃ�
���镡�G�Ȋ��ɂ����āA�Ⴆ��A�̐��E�̌��ۂ�B�̐��E�̊��ɕϊ����Ă����Ă��������ʂ����悭����Ƃ������A������������Ȋ����̐��w�I�_�@�Ƀt�[���G�ϊ��ƌĂ����̂�����܂��B
��ʓI�ɂ��̌`�͐ϕ��̌`�ŕ\����A�͈͂�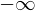 ����
����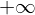 �̐ϕ��̈�̌`�ŕ\������܂��B
�̐ϕ��̈�̌`�ŕ\������܂��B
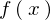 ���l���A������
���l���A������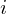 �������P�ʂƂ����
�������P�ʂƂ����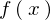 �̃t�[���G�ϕ��\���́A
�̃t�[���G�ϕ��\���́A
���̎���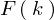 ��
��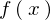 �̃t�[���G�ϊ��ƌ����ċ�̓I�ɂ͎��̂悤�ɕ\���܂��B
�̃t�[���G�ϊ��ƌ����ċ�̓I�ɂ͎��̂悤�ɕ\���܂��B
�Ⴆ�o���h�̉��t�Ȃɂ����Ă���炪�{�[�J���A�h�����A�x�[�X�A�M�^�[�̎l�̃n�[���j�Y���j����ċȂ��o���オ���Ă���Ƃ���ꍇ�A���̒�����M�^�[�̕����݂̂ɒ��ڂ������Ă�������R�s�[�ʼn�͂��ăX�R�A�u�b�N�ɏ����o���悤�ȍ�ƂƂ����������ɑ�̎��Ă��܂��i�Ⴆ����Ă����炷�݂܂���j�B
��ʓI�ɂ��̌`�͐ϕ��̌`�ŕ\����A�͈͂�
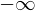 ����
����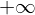 �̐ϕ��̈�̌`�ŕ\������܂��B
�̐ϕ��̈�̌`�ŕ\������܂��B
�����
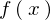 ���l���A������
���l���A������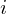 �������P�ʂƂ����
�������P�ʂƂ����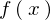 �̃t�[���G�ϕ��\���́A
�̃t�[���G�ϕ��\���́A
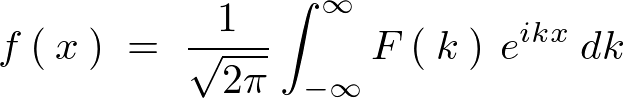
���̎���
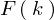 ��
��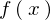 �̃t�[���G�ϊ��ƌ����ċ�̓I�ɂ͎��̂悤�ɕ\���܂��B
�̃t�[���G�ϊ��ƌ����ċ�̓I�ɂ͎��̂悤�ɕ\���܂��B
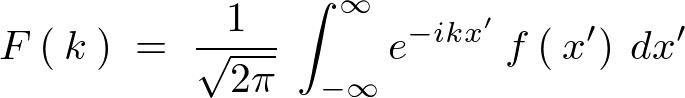
��j
�����Ŏ��Ɏ������悤�Ȃ�������l���܂��B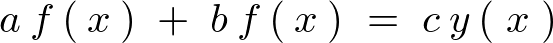
����ɑ��Ď��ۂɃt�[���G�ϊ����Ă݂�ƁA
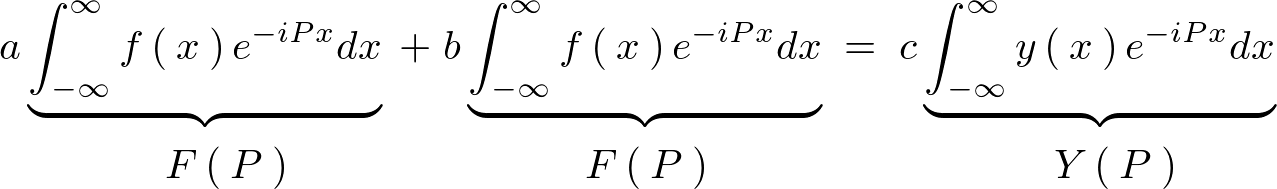
������A
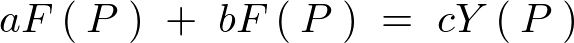
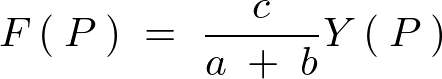
 �̐��E�̌��ۂ�
�̐��E�̌��ۂ�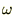 �̐��E�̌��ۂɒu��������Ă��܂��B��������ƍ��܂�
�̐��E�̌��ۂɒu��������Ă��܂��B��������ƍ��܂� �̐��E�Ō��Ă����ꍇ�킩�肸�炩�������̂��A
�̐��E�Ō��Ă����ꍇ�킩�肸�炩�������̂��A �ɒu������邱�ƂŌ��ʂ������邭�Ȃ�A���̌��ۂ��킩��₷���Ȃ�Ƃ������_������܂��B
�ɒu������邱�ƂŌ��ʂ������邭�Ȃ�A���̌��ۂ��킩��₷���Ȃ�Ƃ������_������܂��B
���̑��̐���
�܂�����ɂ͎w������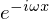 �ɂ͎��Ɏ����悤�ȁA
�ɂ͎��Ɏ����悤�ȁA
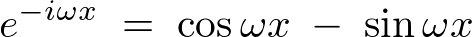
�Ƃ������`�ɕϊ��ł���̂ł�������ɑ������ƁA
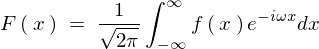
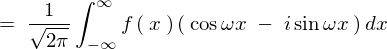
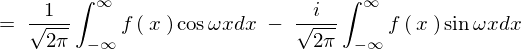
���̏�L���ɂ�����
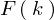 �������ł���ΉE�ӑ�2���͂O�A����ł���ΉE�ӑ�1���̂ق����O�ɂȂ�Ƃ�������������܂��B
���̐����͂��̌�ɏo�Ă���K�E�X���̃t�[���G�ϊ��v�Z���ɂ����ė��p���܂��̂łƂ肠���������������̂ȂȂƂ��������Ŋo���Ă����Ă��������B
�������ł���ΉE�ӑ�2���͂O�A����ł���ΉE�ӑ�1���̂ق����O�ɂȂ�Ƃ�������������܂��B
���̐����͂��̌�ɏo�Ă���K�E�X���̃t�[���G�ϊ��v�Z���ɂ����ė��p���܂��̂łƂ肠���������������̂ȂȂƂ��������Ŋo���Ă����Ă��������B
�K�E�X�ϕ�
�K�E�X�ϕ��̊T�v
������Ԃɂ�����ϕ��ő��ɃK�E�X�ϕ��ƌ�������̂�����܂��B
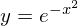 ��`�悵�����̂ł��B
��`�悵�����̂ł��B
���}�͎w����
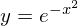 ��`�悵�����̂ł��B
��`�悵�����̂ł��B
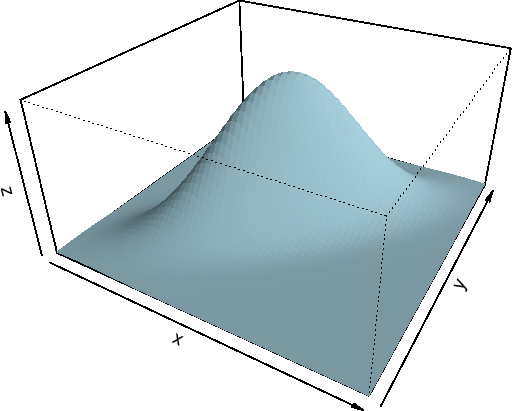
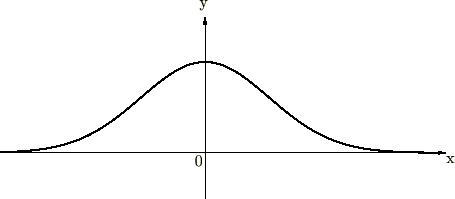
�܂��ϕ�����͈͂�
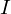 �ƒu���܂��B����
�ƒu���܂��B����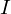 ��2�悵�����̂ɑ��ċɍ��W��K�p������ƁA
��2�悵�����̂ɑ��ċɍ��W��K�p������ƁA
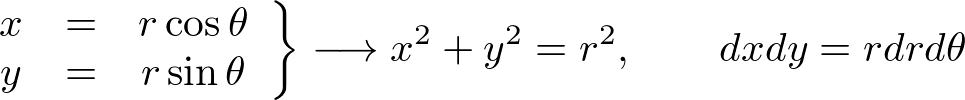
�̂悤�ɂȂ�܂����A�����Ŏ��̂悤�ɍ��W�����݂��Ɍ����������́A
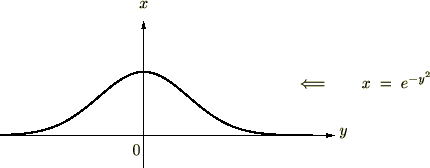
�Ƃ��Ă��������߂�ϕ��͈͂��Ƃ������Ƃ��킩��܂��B
�Ȃ̂Ŏ��̂悤�ɋ��߂�ϕ�����ό`�����邱�Ƃ��\�ɂȂ�܂��B
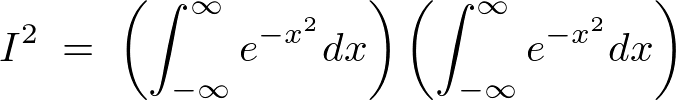
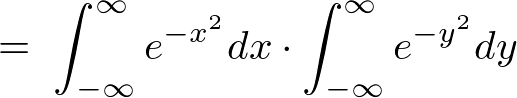
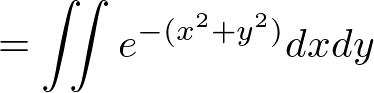
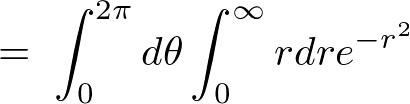
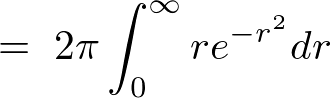
������
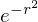 �̕�����
�̕�����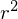 ��
�� �ƒu���܂��B
�ƒu���܂��B
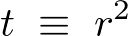
������������
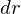 �̕ϊ��i�u���j�����܂��B
�̕ϊ��i�u���j�����܂��B
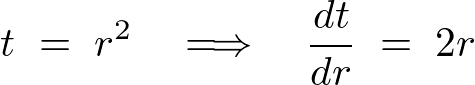
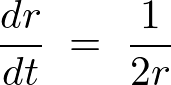
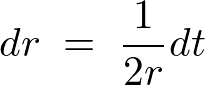
�u��������������̎��ɑ�����܂��B
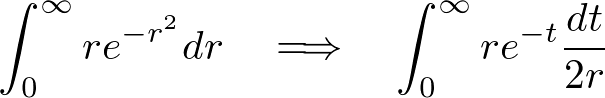
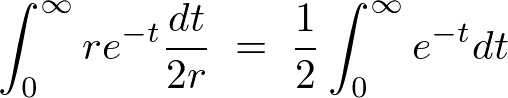
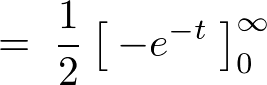
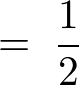
���̌��ʂɂ��
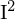 �́A
�́A
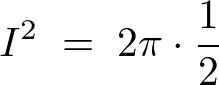

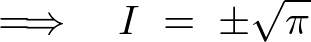
�v���X�̂ق����Ƃ�A
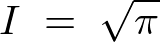
�K�E�X�ϕ��̃t�[���G�ϊ�
���̂悤�ȃK�E�X�����l���܂��B
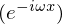 �����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
�����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
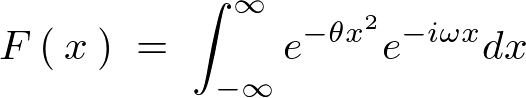

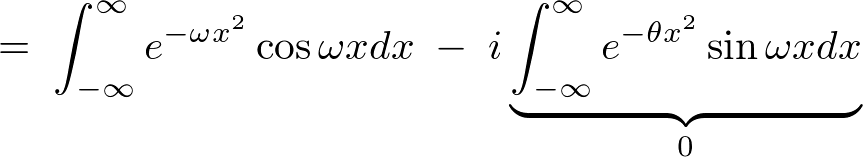
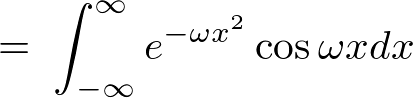
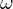 �Ɋւ��Ă̕Δ������s���܂��B
�Ɋւ��Ă̕Δ������s���܂��B
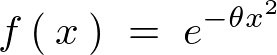
���̃K�E�X���Ɋւ��ăt�[���G�ϊ�
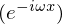 �����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
�����Ă������ꍇ�ǂ̂悤�ȕ������������邩���l�@���Ă����܂��B
�t�[���G�ϊ����́A
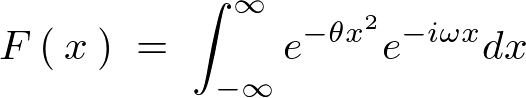
�����Ŏ��̂悤�Ȑ����A
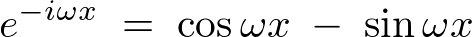
����������Čv�Z���Ă����܂��B
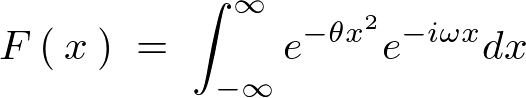

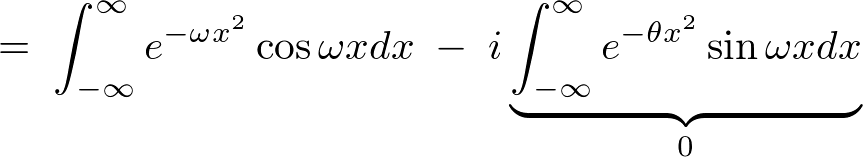
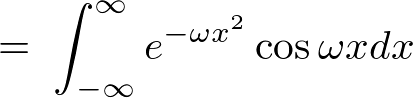
�����ŏo�Ă����ϕ��������̂悤�ɒu���܂��B
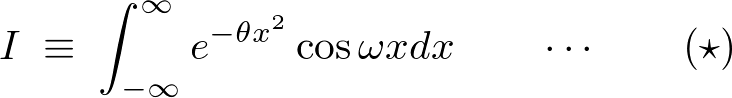
���̎��ɑ��Ď��̂悤��
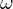 �Ɋւ��Ă̕Δ������s���܂��B
�Ɋւ��Ă̕Δ������s���܂��B
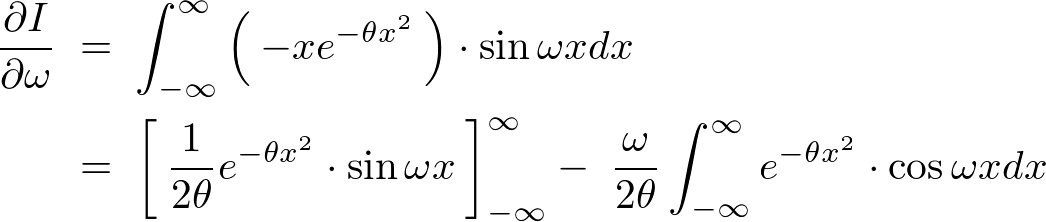
������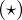 ���A
���A
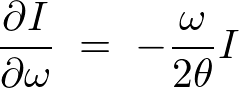
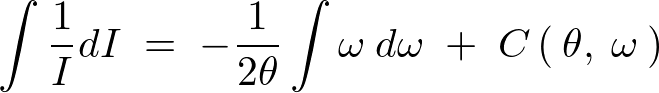
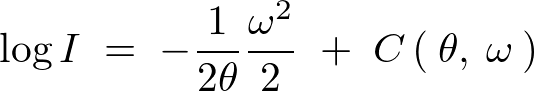
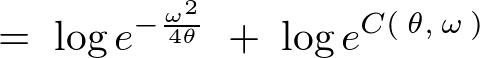
 ���A
���A
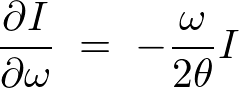
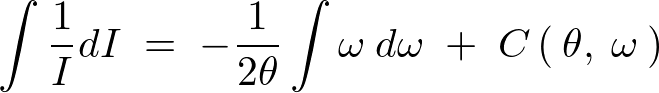
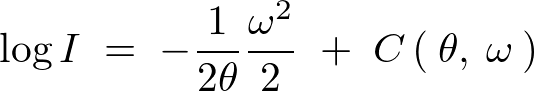
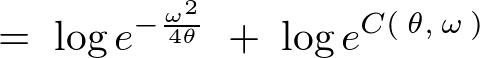
����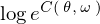 ��������
��������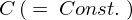 �ƒu���A���������̓I��
�ƒu���A���������̓I��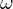 ���O�Ƃ����萔
���O�Ƃ����萔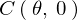 �����߂Ă����B
�����߂Ă����B
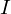 �����ɖ߂��A
�����ɖ߂��A
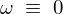 �Ƃ���A
�Ƃ���A
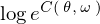 ��������
��������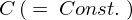 �ƒu���A���������̓I��
�ƒu���A���������̓I��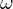 ���O�Ƃ����萔
���O�Ƃ����萔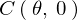 �����߂Ă����B
�����߂Ă����B
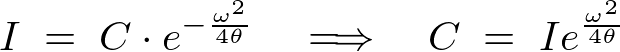
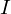 �����ɖ߂��A
�����ɖ߂��A
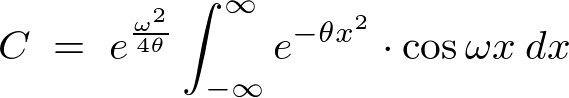
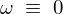 �Ƃ���A
�Ƃ���A
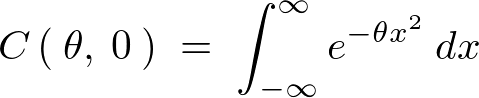
�K�E�X�ϕ����o�Ă���̂ł�����قǂ̂����œ����悤�Ɍv�Z���Ă����܂��B
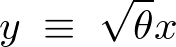
�ƒu���ĕϐ��ϊ��A
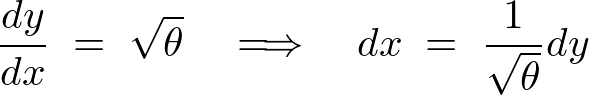
������Ă����܂��B
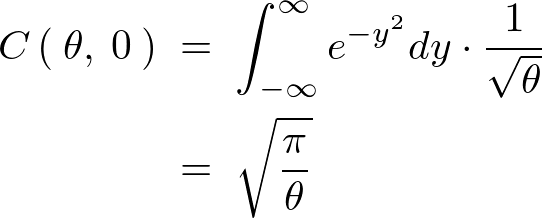
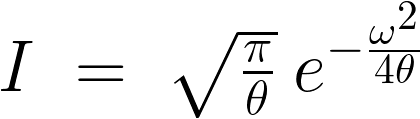
����ăK�E�X���̃t�[���G�ϊ��͎��̂悤�ɋ��܂�܂��B
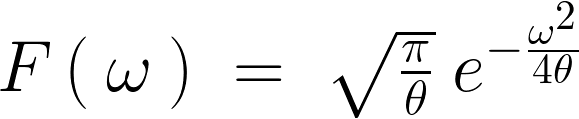
�K�E�X���̃t�[���G�ϊ��֘A�y�[�W
- �f���^���̃t�[���G�ϊ�
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �t�[���G�ϊ�
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �t�[���G�����W�J
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ��|�Ƃ��Ă͒ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B�܂��g�b�v���x���h���C�������̓u���O�^�R���e���c�ɂȂ��Ă���u���O�`���̃R���e���c�͐��w�ȊO�̃e�[�}����Ɉ����܂��B























