�t�[���G�ϊ��̎�
�܂��͂����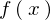 ���l���A������
���l���A������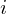 �������P�ʂƂ����
�������P�ʂƂ����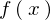 �̃t�[���G�ϕ��\���́A
�̃t�[���G�ϕ��\���́A
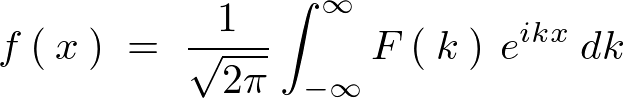
���̎���
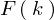 ��
��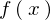 �̃t�[���G�ϊ��ƌ����ċ�̓I�ɂ͎��̂悤�ɕ\���܂��B
�̃t�[���G�ϊ��ƌ����ċ�̓I�ɂ͎��̂悤�ɕ\���܂��B
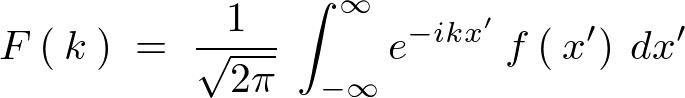
�Ƃ����̂͑O�ɂ���������
�f���^��
�����Ńf���^���Ƃ������̂����l�@���܂��B���̃f���^���Ƃ����̂�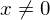 �A�܂�
�A�܂�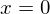 �ȊO�̏ꏊ�ɂ����Ă̒l�͂��ׂĂO�ŁA
�ȊO�̏ꏊ�ɂ����Ă̒l�͂��ׂĂO�ŁA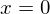 �ł݂̂��̒l��
�ł݂̂��̒l��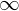 �ƂȂ�A�����̖ʐς��g�P�h�ɂȂ�ƒ�`�������ł��B
�ƂȂ�A�����̖ʐς��g�P�h�ɂȂ�ƒ�`�������ł��B
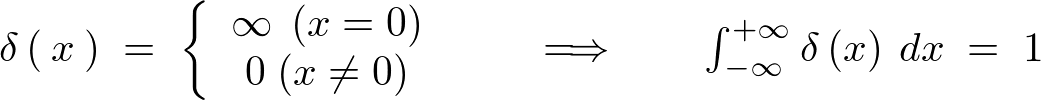
���f���^���̂��̑��̕\�����F�t�[���G�ϕ��\��
����R������ԁi�o��ԁj�ɂ����Ď��̂悤�ɕ\��������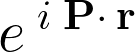
���l������ɑ���
 �i�O���f�B�G���g�j��
�i�O���f�B�G���g�j�� �i�_�C�o�[�W�F���X�j�Ȃǂ���p�����ό`���Ă����܂��i����ɂ��Ă̏ڂ����������x�N�g��������Q�Ƃ��Ă��������j�B
�i�_�C�o�[�W�F���X�j�Ȃǂ���p�����ό`���Ă����܂��i����ɂ��Ă̏ڂ����������x�N�g��������Q�Ƃ��Ă��������j�B
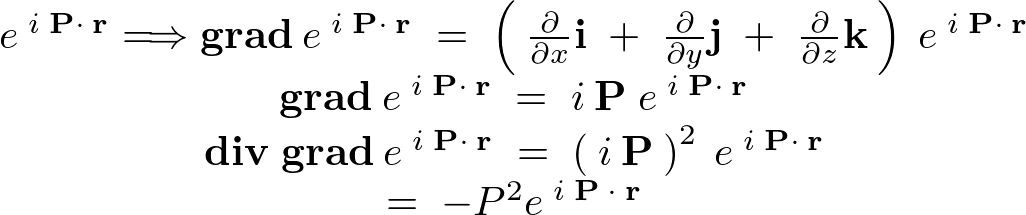
���v���V�A�����g���Ď��̂悤�ɕ\���܂��B
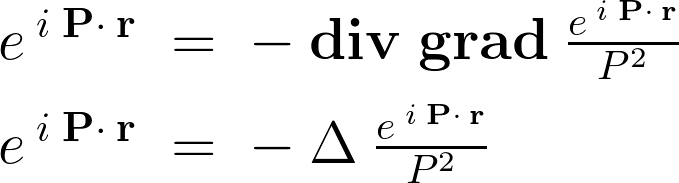
����̐ϕ��̈��S��ԂƂ��ĕ\������Ǝ��ɂ悤�ɂȂ�B
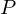 ��Ԃ̋ɍ��W�ɕϊ����܂��B������
��Ԃ̋ɍ��W�ɕϊ����܂��B������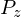 ����
����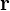 �̕����ɂȂ�悤�ɂƂ���̔��������̃��R�r�A���́A
�̕����ɂȂ�悤�ɂƂ���̔��������̃��R�r�A���́A
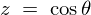 �ƒu���A�����
�ƒu���A�����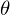 �Ŕ��������
�Ŕ��������
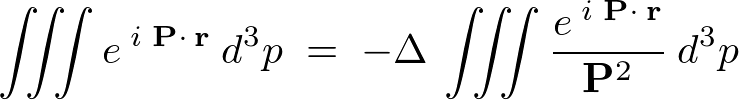
������
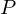 ��Ԃ̋ɍ��W�ɕϊ����܂��B������
��Ԃ̋ɍ��W�ɕϊ����܂��B������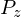 ����
����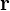 �̕����ɂȂ�悤�ɂƂ���̔��������̃��R�r�A���́A
�̕����ɂȂ�悤�ɂƂ���̔��������̃��R�r�A���́A
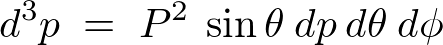
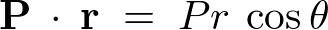
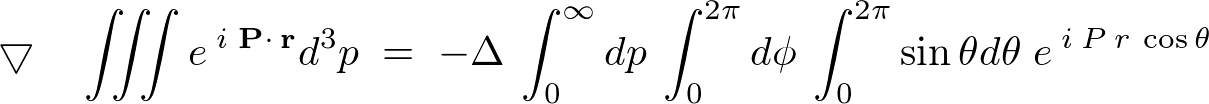
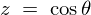 �ƒu���A�����
�ƒu���A�����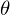 �Ŕ��������
�Ŕ��������
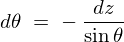
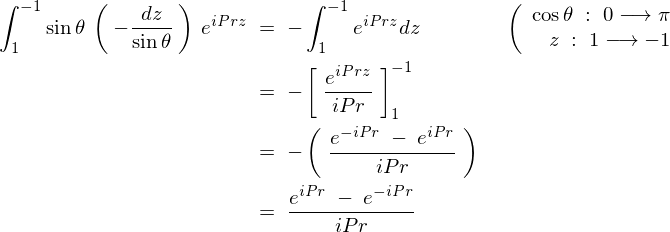
�����ŎO�p���̐����A
�ɂ��A
���g���A
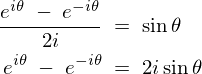
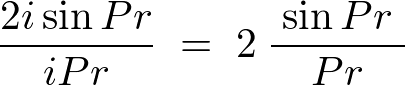
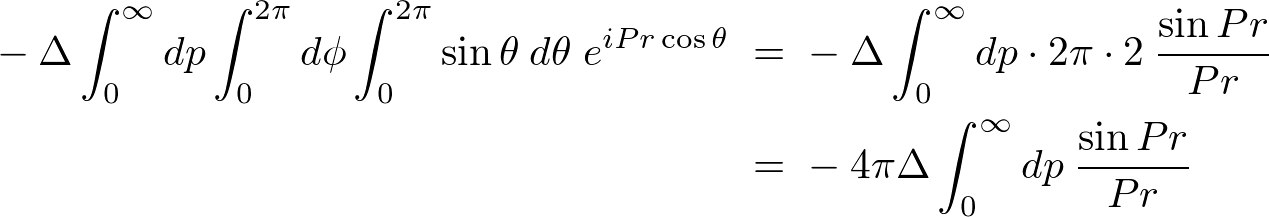
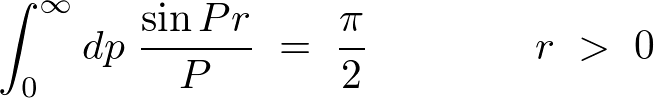
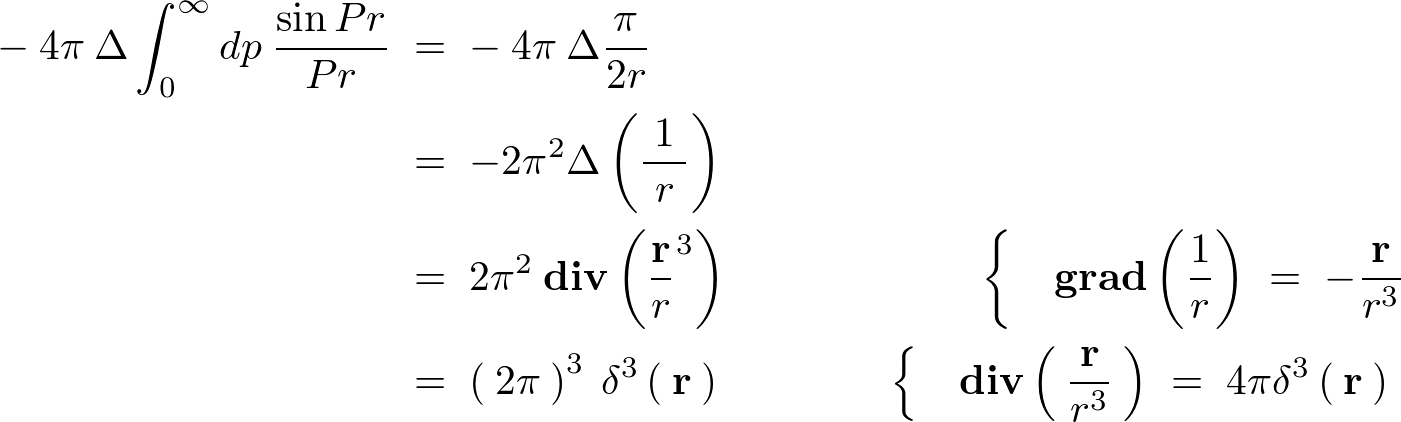
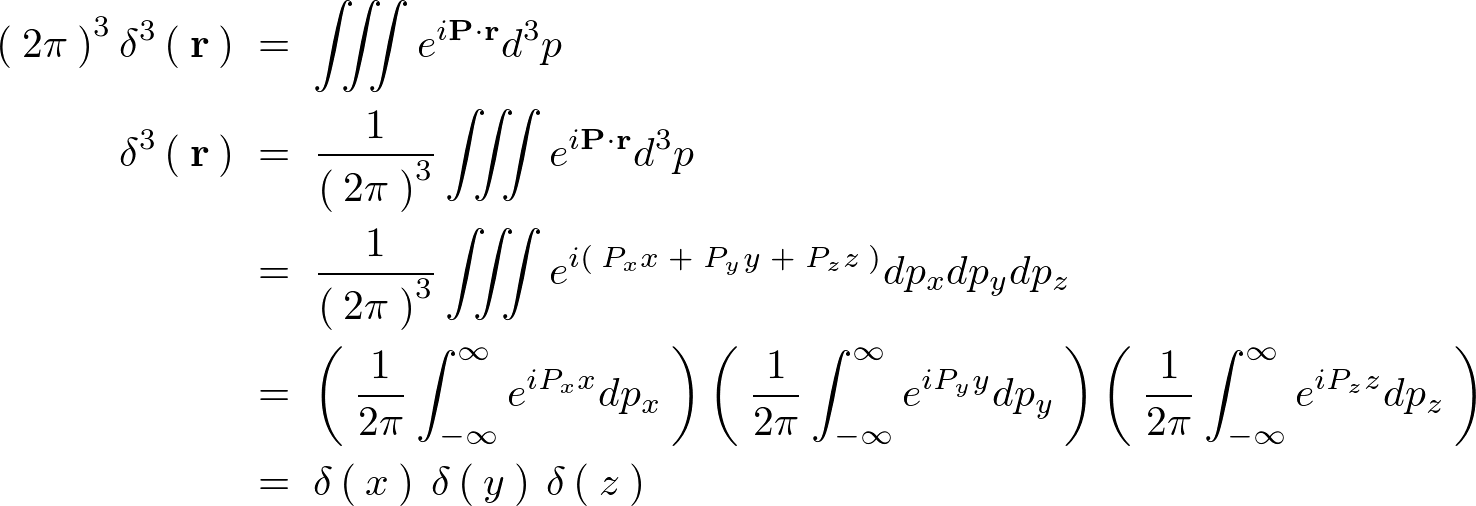
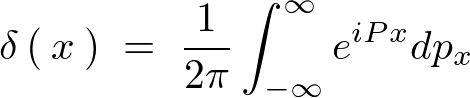
�f���^�����g�����t�[���G�ϊ����̋��ߕ�
�������ł��̃f���^��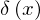 �ɂ�����
�ɂ�����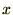 ������
������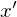 ���������ړ��������Ƃ���f���^��
���������ړ��������Ƃ���f���^��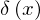 �́A
�́A
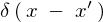
������g���ΐ�قǂ̈ꎟ���f���^���͎��̂悤�ɕ\���ł��܂��B
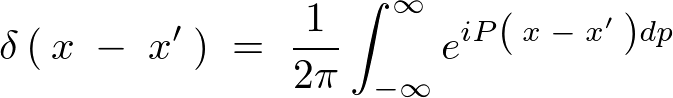
��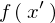 �ɂ����ċ��
�ɂ����ċ��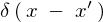 �Ƃ̐ς�
�Ƃ̐ς�
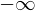 ����
����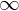 �ɂ����Đϕ������s����A
�ɂ����Đϕ������s����A
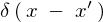 �������܂��B
�������܂��B
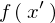 �ɂ����ċ��
�ɂ����ċ��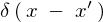 �Ƃ̐ς�
�Ƃ̐ς�
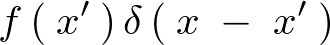
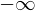 ����
����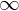 �ɂ����Đϕ������s����A
�ɂ����Đϕ������s����A
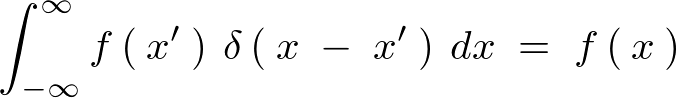
���̎���
 �������܂��B
�������܂��B
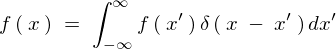
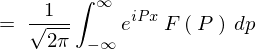
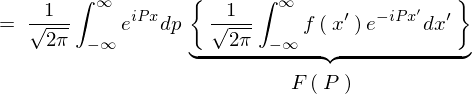
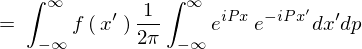
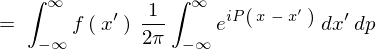
���ʂƂ��Ď��̂悤�ɋ��܂�B
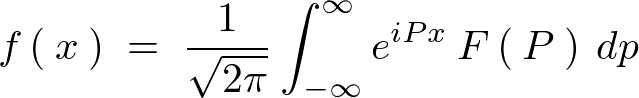
�o�Ă����������Ă킩��悤�ɏ�L���ό`���ɂ����ďo�Ă������������ʂ̂Ȃ��̂��͍̂ŏ��Ɏ������t�[���G�ϊ����ł��B�����ĉE�ӂ̈�ԍŌ�ɏo�Ă��������t�[���G�t�ϊ��̎��Ƃ����܂��B
| �t�[���G�ϊ� | 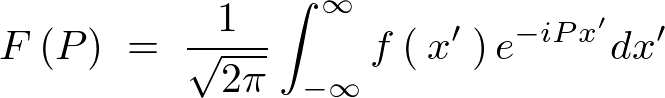 |
|---|---|
| �t�[���G�t�ϊ� | 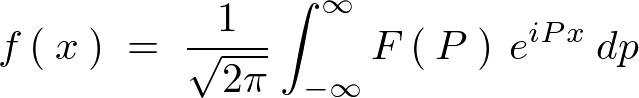 |
�f���^���̃t�[���G�ϊ��֘A�y�[�W
- �K�E�X���̃t�[���G�ϊ�
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �t�[���G�ϊ�
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B
- �t�[���G�����W�J
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ��|�Ƃ��Ă͒ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B�܂��g�b�v���x���h���C�������̓u���O�^�R���e���c�ɂȂ��Ă���u���O�`���̃R���e���c�͐��w�ȊO�̃e�[�}����Ɉ����܂��B























