�x�N�g���O�ρ|�b���������@�o������������
�x�N�g����̉�]
�����Ȃ̈�N���ɏK���x�N�g����͂ɂ����āA

�͂قƂ�ǂ̃e�L�X�g�ł͂R�s�R��̍s�ɕ\�L���Ă���Ǝv���܂��B�����Ă��̏ꍇ�A���ۂ̌v�Z�ł̓T���X�ʼn������A���邢�͍s��\�L�ł͂Ȃ����̌����̂悤�Ȃ��̂��ËL���Ă���ꍇ���������邩�Ǝv���܂��B
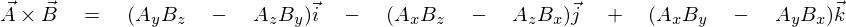
���̃x�N�g���ς��s�W�J�@�ʼn����Ă����܂��B
���̕ό`
�x�N�g���ρi�b���������o�������������j�̍s�̕\�L�͂��̂悤�������Ǝv���܂��B
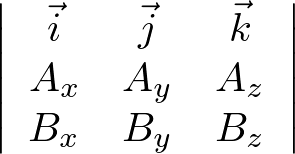
�I�y���C�g�����p�f�������ɒu���Ƃ������`�ɂ���A
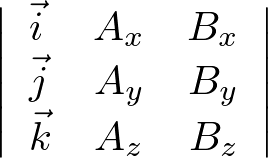
���̂悤�ɂ���ΐ�قǂ̍s�W�J�@�̒�`�����̂܂g���܂��i�ό`�����ɍs�W�J�@�̒�`�ł��̂܂܌v�Z�����Ƃ��Ă����ʂ͓����ł��j�B
��������Ă݂�ƁA
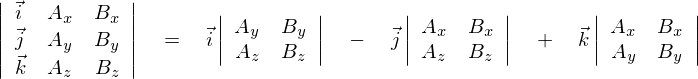
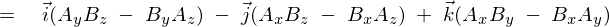
�ƂȂ�܂��B
���͎��ۂɃx�N�g���O�ς̌v�Z�����Ă݂܂��傤�B
���
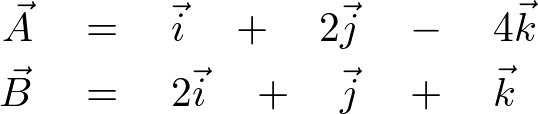
�Ƃ��܂��B
���̊O�ς��v�Z���Ă݂܂��傤�B

����
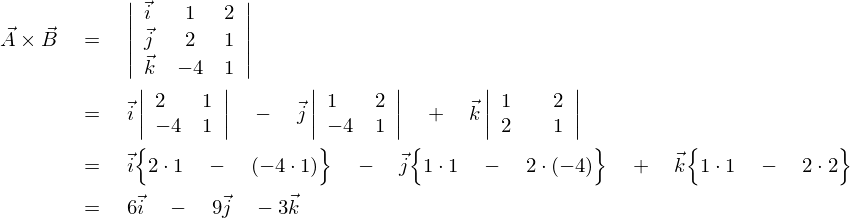
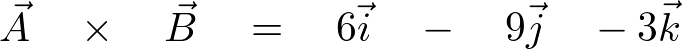
�x�N�g���O�ϊ֘A�y�[�W
- �x�N�g����̉�]
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B


























