�u���b�N�V���[���Y���f������������
�����ŕϐ��ϊ�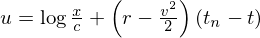 �̎��������̃P�[�X�ɒu�������čl�����
�̎��������̃P�[�X�ɒu�������čl�����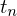 �Ƃ����̂̓R�[���I�v�V�����Ȃǂ̖������ɂ�����̂Łi���͐��w��ł͉\�ł����j�����ɂ�
�Ƃ����̂̓R�[���I�v�V�����Ȃǂ̖������ɂ�����̂Łi���͐��w��ł͉\�ł����j�����ɂ�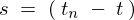 �̒l�i���ԁj�̓}�C�i�X�ɂȂ�Ƃ������Ƃ͂���܂���B
�̒l�i���ԁj�̓}�C�i�X�ɂȂ�Ƃ������Ƃ͂���܂���B
�����čŏ��̋��E������ �Ƃ����͖̂������}���������Y���i
�Ƃ����͖̂������}���������Y���i ���s�g���i
���s�g���i ���傫���Ƃ��������Ȃ̂�
���傫���Ƃ��������Ȃ̂�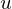 ��
��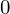 �ȉ��Ȃ���Z�h�����i
�ȉ��Ȃ���Z�h�����i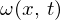 �̉��l��
�̉��l��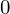 �A����ɂ͖������ɂ����鋫�E������
�A����ɂ͖������ɂ����鋫�E������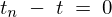 �ɂȂ�̂�
�ɂȂ�̂�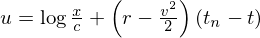 �̎��ɑ������A
�̎��ɑ������A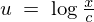 �ƂȂ�܂��B
�ƂȂ�܂��B
�����ό`����ƁA
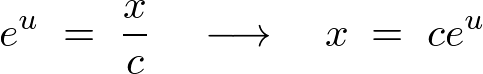
�ƂȂ�܂��B�ł��̂ňȏ�̌��ʂ��l������A�ŏ��Ɏ��������E�����́A
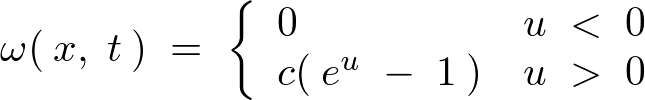
����ɐ�قǂ̕ϐ��ϊ��Ɋւ��čl������A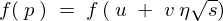 �ł���A
�ł���A �Ƃ��Ă���̂ŁA���̋��E�����͂���ɁA
�Ƃ��Ă���̂ŁA���̋��E�����͂���ɁA
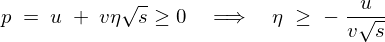
���A
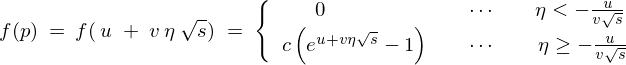
 �̒l��
�̒l��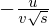 �ȉ��Ȃ��
�ȉ��Ȃ�� �̒l��
�̒l��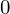 �ł���A���̏ꍇ�ϕ�����͈͂�
�ł���A���̏ꍇ�ϕ�����͈͂�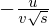 �ȏ�Ɍ����܂��B
�ȏ�Ɍ����܂��B
�Ȃ̂Őϕ��͈͂�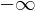 ����
����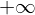 �ƂȂ��Ă��܂����A(5.3.4)�̐ϕ��͎��̂悤�ɕ\���ł��܂��B
�ƂȂ��Ă��܂����A(5.3.4)�̐ϕ��͎��̂悤�ɕ\���ł��܂��B
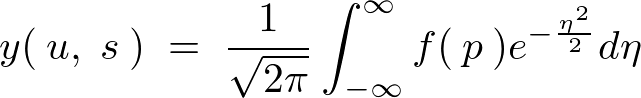
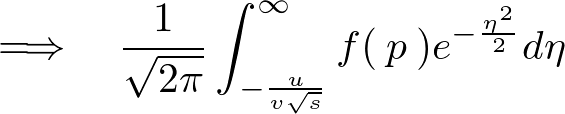
����ɏ�L�͈͓��ɂ���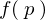 �Ă͂߂�Ύ��̂悤�ɂȂ�܂��B
�Ă͂߂�Ύ��̂悤�ɂȂ�܂��B
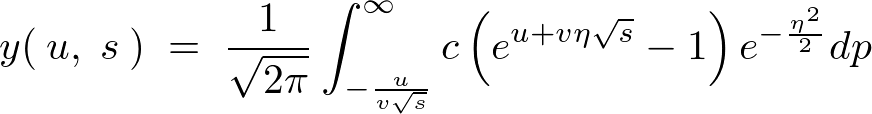
 �����ɂ��ǂ��A��L�̎���ό`�����܂��B
�����ɂ��ǂ��A��L�̎���ό`�����܂��B
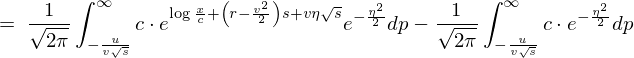
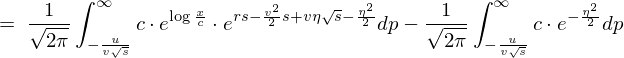
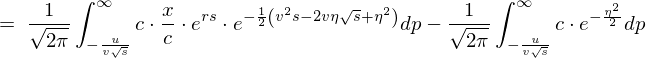
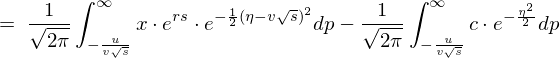
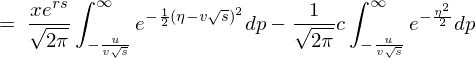
������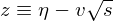 �ƒu���ϐ��ϊ������{���܂��B
�ƒu���ϐ��ϊ������{���܂��B
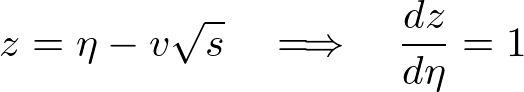
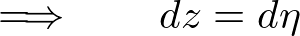
��������
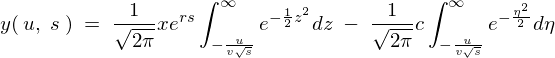
�����ŕϊ�����O��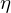 �̐ϕ��͈͂�
�̐ϕ��͈͂�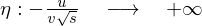 �ł����A�����ϐ��ϊ����
�ł����A�����ϐ��ϊ����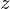 �ɒu�������Ă݂�Ǝ��̂悤�ɂȂ�܂��B
�ɒu�������Ă݂�Ǝ��̂悤�ɂȂ�܂��B
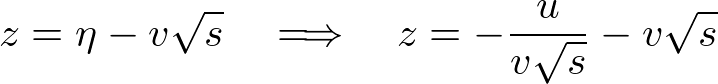
�Ȃ̂Őϕ��͈͂́A
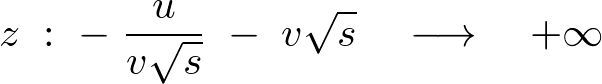
 �͈͎̔͂��̂悤�ɂȂ�܂��B
�͈͎̔͂��̂悤�ɂȂ�܂��B
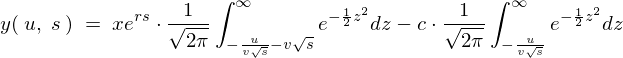
�\�L�ꂷ�邽�߂ɂQ���ڂ�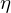 ��
��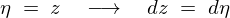 �Ƃ��ĕϐ��ϊ������Ă��܂��B
�Ƃ��ĕϐ��ϊ������Ă��܂��B
�����ʼn��̃O���t���l�@���܂��B
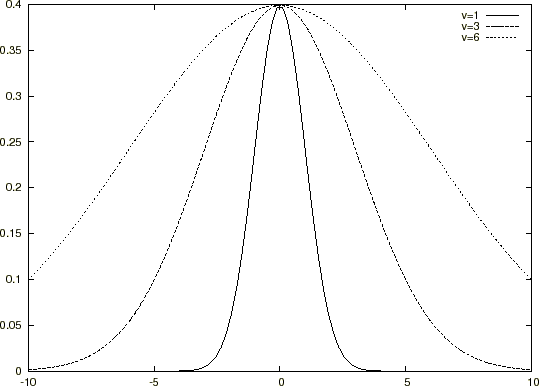
����́A
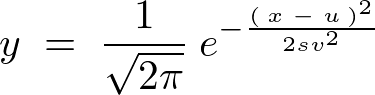
�Ƃ������ɂ�����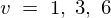 �̒l�ɂ����邻�ꂼ��̃O���t��\�������̂ł��B
�̒l�ɂ����邻�ꂼ��̃O���t��\�������̂ł��B
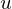 �͕��ρA
�͕��ρA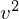 �͕��U��\���Ă��܂��B
�͕��U��\���Ă��܂��B
�Ȃ��A ��
��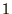 �Ƃ��Ă��܂��B
�Ƃ��Ă��܂��B
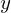 ���𒆐S�ɂ��Ă��̌`�����E�Ώ̂ɂȂ��Ă���̂��킩��Ǝv���܂��B
���𒆐S�ɂ��Ă��̌`�����E�Ώ̂ɂȂ��Ă���̂��킩��Ǝv���܂��B
���̊��͐��K���z���Ƃ����Ă���A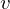 �̒l���ω����O���t�̌`�͕ς���Ă����̍��E�Ώ̂Ƃ����\���͕ς���Ă��Ȃ��Ƃ����̂����̑傫�ȓ����ł��B
�̒l���ω����O���t�̌`�͕ς���Ă����̍��E�Ώ̂Ƃ����\���͕ς���Ă��Ȃ��Ƃ����̂����̑傫�ȓ����ł��B
���̊��͈�ʓI�Ɏ��̂悤�Ȋȗ��������\�L�����܂��B
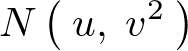
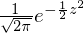 �ɑ��Ă��������Ƃ������܂��i�E���O���t���E��̎���
�ɑ��Ă��������Ƃ������܂��i�E���O���t���E��̎��� �ɑΉ�����̂�
�ɑΉ�����̂�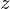 �ł��j�B
�ł��j�B
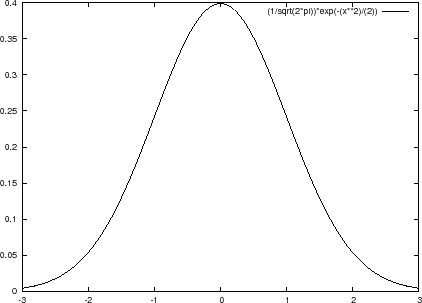
���K���z���̂����������������p����Ύ��̂悤�Ȃ��Ƃ������܂��B
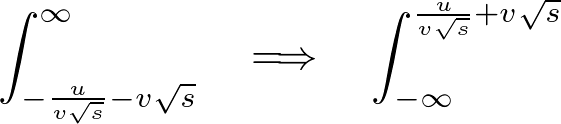
������A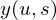 �ɂ����邱�̊��𐳋K���z���\�L���g���ĕ\���Ύ��̂悤�ɂȂ�܂��B
�ɂ����邱�̊��𐳋K���z���\�L���g���ĕ\���Ύ��̂悤�ɂȂ�܂��B
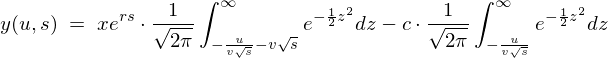
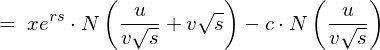
�Ō�� �ɑ�����܂��B
�ɑ�����܂��B
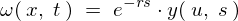
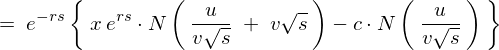
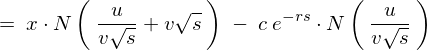
����Ď��̂悤�ɋ��܂�܂��B
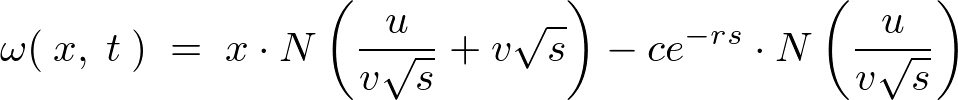
�u���b�N�V���[���Y���f���Δ����������֘A�y�[�W
- �u���b�N�V���[���Y���f���\�����������̓��o
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B
- �u���b�N�V���[���Y���f���\�L���v�f�@
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B
- �u���b�N�V���[���Y���f���[�ϕ����̕ϊ�
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B

























