�M�`���������̕ϐ�����
�O�Z�N�V�����ɂē��o���ꂽ�ꎟ���M�`���������Ɋւ��āA�ϐ������Ƃ�����Ƃ��s���ď��X�Ɍv�Z�����s���Ă����܂��B
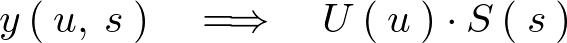
�Ƃ��܂��B
����ƁA
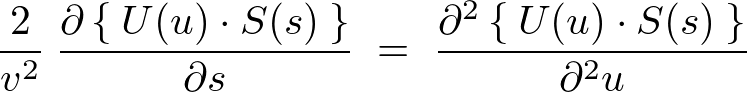
�ƂȂ�̂ŁA�����ŕϐ��������s���ƁA
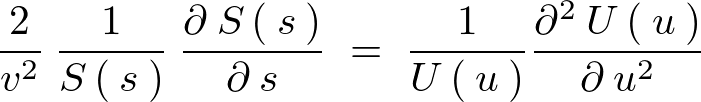
���Ă킩��悤�ɗ��ӂ̎��͂��݂��̂��ꂼ��̕ϐ��Ɉˑ����Ă��Ȃ��`�ɂȂ��Ă��܂��B
�ł��̂Ŏ��̂悤�ɒu�����Ƃ��\�ɂȂ�܂��B
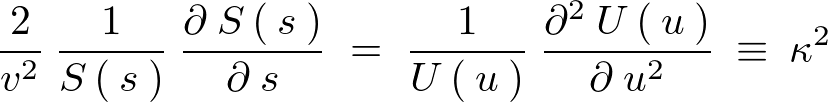

����Ɏ��̂悤�ɒu���܂��B
(5.2.2)�̎������̂悤�ɕό`���܂��B
���̔����������̉��Ƃ��Ă͂R�قǍl�����܂����M�`���̃Z�N�V�����ł�����悤�ɂ��̏ꍇ�A�L�����Ӗ��̂����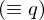 �́A
�́A
�ɂȂ�܂��B
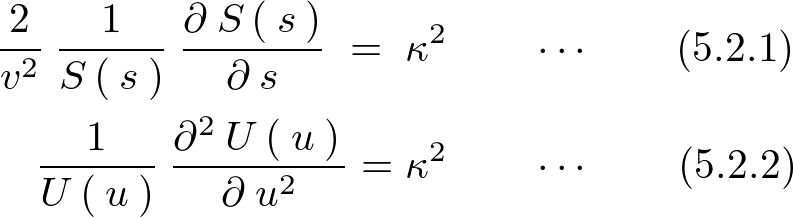
(5.2.2)�̎������̂悤�ɕό`���܂��B
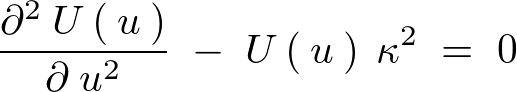
���̔����������̉��Ƃ��Ă͂R�قǍl�����܂����M�`���̃Z�N�V�����ł�����悤�ɂ��̏ꍇ�A�L�����Ӗ��̂����
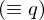 �́A
�́A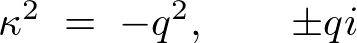
�ɂȂ�܂��B
��������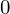 �A��������
�A��������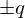 �Ȃ̂œ����������̉��͎��̂悤�ɂȂ�܂��B
�Ȃ̂œ����������̉��͎��̂悤�ɂȂ�܂��B
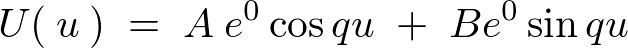
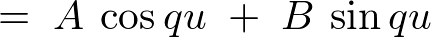
�����ŏo�Ă����萔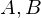 �����ꂼ��
�����ꂼ��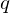 �̊��ƍl���A
�̊��ƍl���A
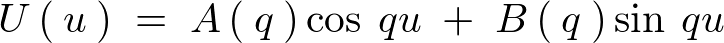
�Ƃ��܂��B
����(5.2.1)�́A
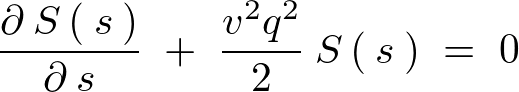
�ƒu����̂ł��̔����������������Ă����܂��B
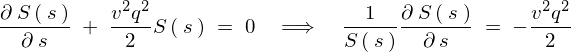
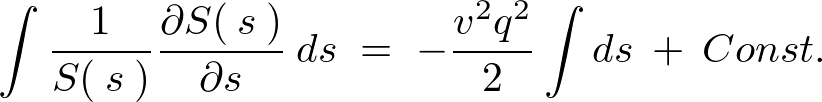
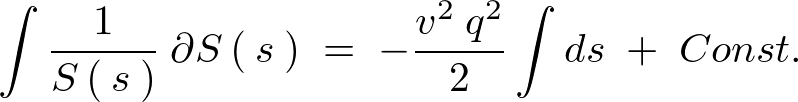
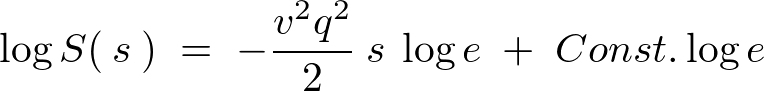
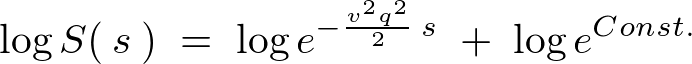
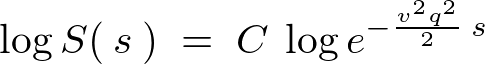
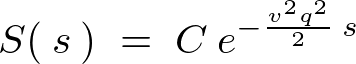
�ƂȂ�܂��B
�����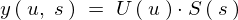 �ɑ������A
�ɑ������A
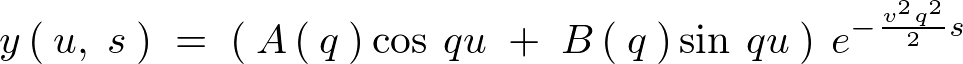
���̕Δ����������̉������ׂĂ��d�ˍ��킹�ƍl����ƁA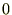 ����̖�����Ԃƍl������̂ł��̉��̔����������́A
����̖�����Ԃƍl������̂ł��̉��̔����������́A
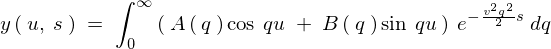
�Əo���܂��B
�Ƃ���Ő�قǂ̔������������^����ꂽ�Ƃ��̏������l�����A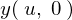 �Ƃ����
�Ƃ����
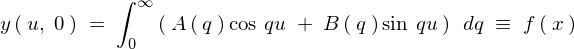
�ƂȂ�A����ɂ���ăt�[���G�ϕ��������K�p�ł���悤�ɂȂ�܂��B
�u���b�N�V���[���Y���f���\�L���v�f�@�֘A�y�[�W
- �u���b�N�V���[���Y���f���\�����������̓��o
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B
- �u���b�N�V���[���Y���f���[�ϕ����̕ϊ�
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B
- �u���b�N�V���[���Y���f������������
- �u���b�N�V���[���Y���f���Ƃ́A���Z�H�w�ɂ�����I�v�V�����̉��i����̍ۂɕK�v�Ȍv�Z���f���̂��Ƃ��w���܂��B���T�C�g�͂��̃u���b�N�V���[���Y�Δ����������̓��o�ƒ낾���ł͂Ȃ����������߂̏������w����J�ɉ�������T�C�g�ɂȂ�܂��B


























