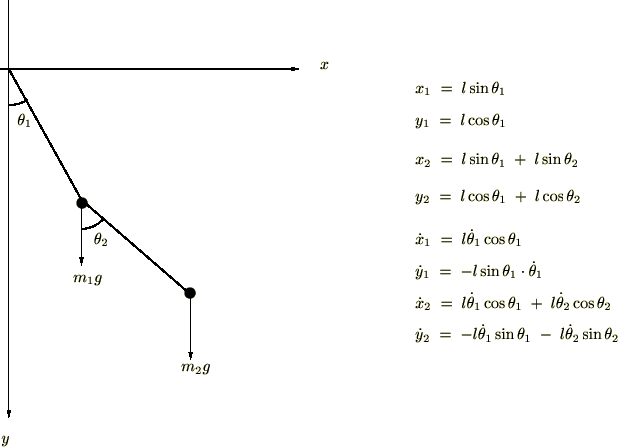���O�����W����
���x �ʼn^�����Ă��鎿��
�ʼn^�����Ă��鎿��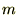 �̉^���G�l���M�[
�̉^���G�l���M�[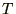 ���f�J���g���W�ŕ\����
���f�J���g���W�ŕ\����
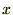 �������݂̂��l���A���̂���̎��Ԃ�
�������݂̂��l���A���̂���̎��Ԃ�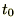 ����
����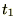 �Ƃ��܂��B
�Ƃ��܂��B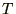 ���̂̎��Ԃɑ���ϕ��Ɣ����̊W�����߂܂��B
���̂̎��Ԃɑ���ϕ��Ɣ����̊W�����߂܂��B
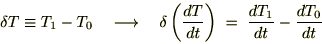
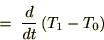
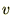 �ʼn^�����Ă��鎿��
�ʼn^�����Ă��鎿��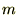 �̉^���G�l���M�[
�̉^���G�l���M�[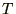 ���f�J���g���W�ŕ\����
���f�J���g���W�ŕ\����
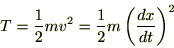
����̕ϕ����l���Ă݂܂��傤�B
�ȒP�̂��߂ɉ^����
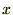 �������݂̂��l���A���̂���̎��Ԃ�
�������݂̂��l���A���̂���̎��Ԃ�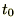 ����
����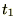 �Ƃ��܂��B
�Ƃ��܂��B�܂�
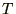 ���̂̎��Ԃɑ���ϕ��Ɣ����̊W�����߂܂��B
���̂̎��Ԃɑ���ϕ��Ɣ����̊W�����߂܂��B
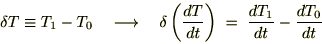
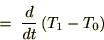

����ɉ^���G�l���M�[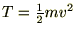 �̕ϕ����l����A
�̕ϕ����l����A
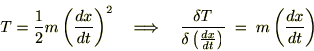
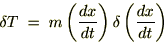
�i1.12�j�Ɂi1.13�j��������ƁA
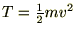 �̕ϕ����l����A
�̕ϕ����l����A
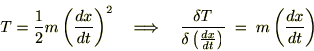
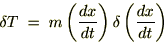

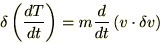
�����ƕϕ��̓���ւ����\�Ȃ̂Ŏ��̂悤�ɂȂ�܂��B
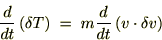

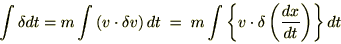
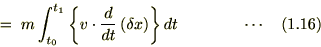
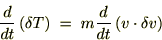

�i1.15�j����ϕ�����ƁA
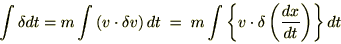
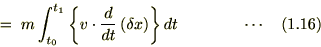
�i1.16�j�ɂ����Ĕ����Ɛϕ����������Ă��܂��B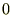 �ɂȂ�Ƃ������Ƃɒ��ӂ���A
�ɂȂ�Ƃ������Ƃɒ��ӂ���A
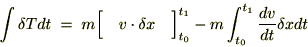

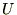 �Ȃǂ̕ۑ��͂������ꍇ
�Ȃǂ̕ۑ��͂������ꍇ
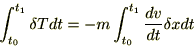 �̎���ό`������ƁA
�̎���ό`������ƁA
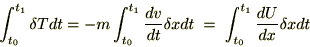
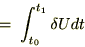
����ɕ����ϕ���K�p���܂����A���̂Ƃ���ꍀ�͒[�_���Œ肵�Ă���̂Ō���
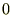 �ɂȂ�Ƃ������Ƃɒ��ӂ���A
�ɂȂ�Ƃ������Ƃɒ��ӂ���A
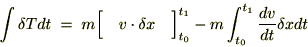

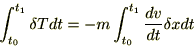
�͂��|�e���V�����G�l���M�[
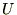 �Ȃǂ̕ۑ��͂������ꍇ
�Ȃǂ̕ۑ��͂������ꍇ

�����Ă���̕ϕ����l�����

�i1.18�j�i1.19�j���g����
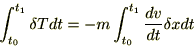 �̎���ό`������ƁA
�̎���ό`������ƁA
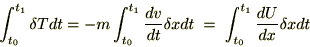
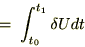
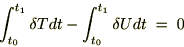
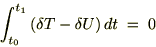
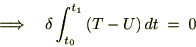
���̂悤�ɒ◯�l���Ƃ点��悤�Ȃ��̂ɂȂ��Ă���A���������^���͂���������̂��ƍl���邱�Ƃ��o���܂��B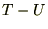 ��
��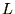 �Ƃ����A�I�C���[�̕������ƑΉ�������A
�Ƃ����A�I�C���[�̕������ƑΉ�������A 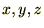 �Ɋg������A
�Ɋg������A
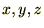 ��
��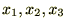 �ƕ\���A
�ƕ\���A
�����ł���
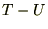 ��
��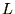 �Ƃ����A�I�C���[�̕������ƑΉ�������A
�Ƃ����A�I�C���[�̕������ƑΉ�������A
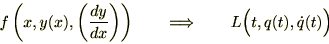

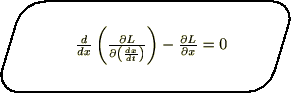
�����
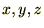 �Ɋg������A
�Ɋg������A
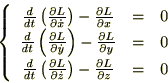
����ɂ�����
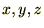 ��
��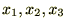 �ƕ\���A
�ƕ\���A
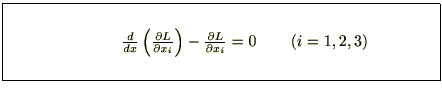
��ʉ��^���ʂ�
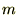 �̉^�����l���Ă݂܂��傤�B
�̉^�����l���Ă݂܂��傤�B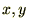 �𐅕��ʂƂ�
�𐅕��ʂƂ�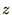 ������������ɍ��W�����܂��B��������ƃ��O�����W�A����
������������ɍ��W�����܂��B��������ƃ��O�����W�A����
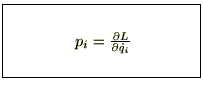
���鎿�_
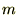 �̉^�����l���Ă݂܂��傤�B
�̉^�����l���Ă݂܂��傤�B
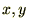 �𐅕��ʂƂ�
�𐅕��ʂƂ�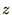 ������������ɍ��W�����܂��B��������ƃ��O�����W�A����
������������ɍ��W�����܂��B��������ƃ��O�����W�A����
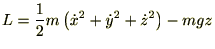
�ƂȂ�̂ł�������O�����W���̎��ɓ��Ă͂߂��
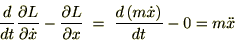
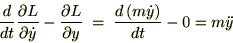
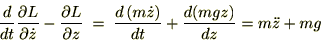
�ƂȂ�̂Ō��ʂ͎��̂悤�ɂȂ�܂��B
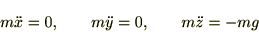
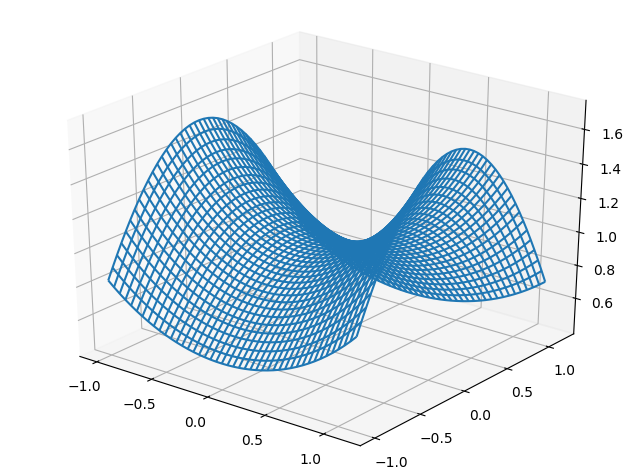
���O�����W�����L���ꗗ
���O�����W���ɂ��A���U���̉��@
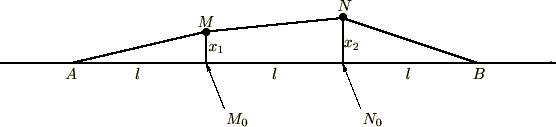 �����̎��͂Œ����Ă����A�������ƂɎ��ʂ̂���������т��A���̂�����͒��p�����݂̂ɐU������Ƃ��܂��B�����������ꍇ�̂�����̏��U�������O�����W�A�����g���ċ��߂Ă݂܂��傤�B
�����̎��͂Œ����Ă����A�������ƂɎ��ʂ̂���������т��A���̂�����͒��p�����݂̂ɐU������Ƃ��܂��B�����������ꍇ�̂�����̏��U�������O�����W�A�����g���ċ��߂Ă݂܂��傤�B
���O�����W���ɂ��A���U���̉��A
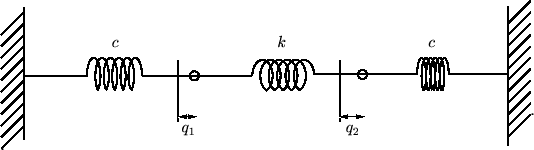 �Ǒ��ɂ��Ă���˂̂˒萔���A�^�̃o�l�̃o�l�萔���Ƃ��A���̃o�l�̋��ɏd���̂�����������ꍇ�̘A���U���̉��B
�Ǒ��ɂ��Ă���˂̂˒萔���A�^�̃o�l�̃o�l�萔���Ƃ��A���̃o�l�̋��ɏd���̂�����������ꍇ�̘A���U���̉��B