�����v�Z�ɂ�鏫���̉��i�i�I���Ƃ����l���j
��ʓI�ɂ������R�Ɨ����݂̂�_���ē��������Ă���Ȃ�ʂł������������������܂łɁA������������ςݗ��ĂĂ��������ƍl����悤�Ȍ����ȉ^�p�ł���ꍇ�A��̂̊��Ԃ��߂ĔN�ԉ����̋�����ݒ肷��Ώ�����������������ɂȂ邩�Ƃ����v�Z���s���ꍇ�����������Ǝv���܂��B�Ⴆ�ΔN�����R���ʼn^�p���Ă������ꍇ�A��N��ɂ͌��{�in�j���܂߂����z�͂��~�P�D�O�R�ɂȂ���̂��Ƃ������̂ł����āA�Ⴆ��100���~����N�ԉ^�p�����103���ɂȂ�܂��B
�����Ă��̋����ɂ͒P���ƕ���������܂��B
������
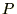 �A�N����
�A�N����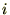 �A�I���Ȃǂ̐��l��
�A�I���Ȃǂ̐��l��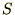 �A����ɗ�����
�A����ɗ�����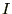 �Ƃ��܂��B
�Ƃ��܂��B���Ԃ�
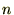 �N�ԂƂ����ꍇ�A���̊��ԓ��ɂ�����P���ɂ�闘��
�N�ԂƂ����ꍇ�A���̊��ԓ��ɂ�����P���ɂ�闘��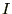 �́A
�́A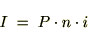
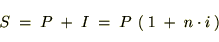
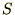 ���قǂ��������I���Ƃ����Ăѕ������܂��B
���قǂ��������I���Ƃ����Ăѕ������܂��B
�����v�Z
�����v�Z�ɂ����Ă͈�N���o�߂����������v������Ɏ��̔N�x�̓��������ɑg�ݓ����Ƃ������̂Ȃ̂ŁA�P�N��̌������v
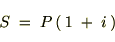
�Q�N��̌������v
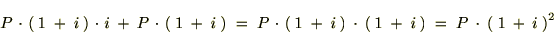
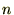 �N��̕����v�Z�ɂ����錳�����v
�N��̕����v�Z�ɂ����錳�����v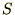 �i�I���j��
�i�I���j��
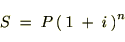
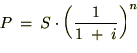
���ɔN���R���A20�N�ԉ^�p�ł����Ƃ��A�I��5000���~�����̂ł���Έȉ��̂悤�Ȍv�Z�ɂȂ�܂��B
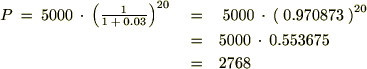
���n�����m��N���I��
��L�̎�������ɔ��W���������Ŋ��n�����m��N���I���Ƃ�������������B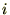 ��N�����A
��N�����A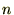 ��N���Ƃ��Ď��̂悤�ɕ\���B
��N���Ƃ��Ď��̂悤�ɕ\���B
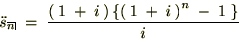

�Q�l�܂łɒNjL����Ǝ��̂悤�Ȃ��̂��B
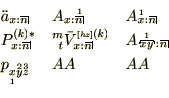
���n�����N���I���W��
ex1.
���ɔN���R���łQ�O�N�ԉ^�p�ł����Ƃ��A���̂Q�O�N��ɂT�O�O�O���~��ڕW�ɂ����Ƃ��܂��B���������ꍇ�̖��N�n�߂ɗp�ӂ�����z��������ɂȂ邩�����ۂɊ��n�����N���I���̎��ɑ�����ē����o���Ă݂܂��傤�B�N���F
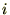 ���R���A�N���F�����Q�O�N
���R���A�N���F�����Q�O�N
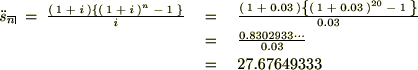
���N�n�߂ɗp�ӂ�����z���gX�h�ƒu���ƁA�I���T�O�O�O���Ȃ̂Ŏ��̂悤�ȍP���������藧��X�����܂�܂��B
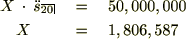
���N���߂ɗp�ӂ�����z����P�W�O���~�B����N�����ʼn^�p���Ă������ꍇ�Q�O�N��ɂ͖ڕW�̋��z�ɒB�����邱�Ƃ��ł��܂��B���������N���������ʼn^�p�ł����ꍇ�ł���A�o�ϊ��͏�����ω����Ă���̂ʼn^�p�������ύX�ɂȂ����ꍇ�͓r���ōH�v����K�v������܂��B
ex2.�r���ŋ����̕ύX�Ȃǂ��������ꍇ
���ɗ��B���Ă�����ԓ��ɂ����ė����̕ύX�Ȃǂ��������ꍇ���l���Ă݂܂��傤�B��Ƃ��ĂR���������������P�O�N��Ɉ��������ɂȂ�Q���ɂȂ����Ƃ��܂��B
��j
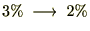
���������ꍇ�A�܂��ύX�O�̂P�O�N�Ԃ̉^�p���ʂ��܂��B
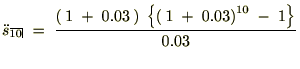
��قǂ̌v�Z����
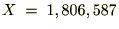 ���
���
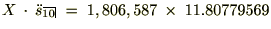
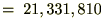
���N�̐ϗ��z�ɂ��P�O�N��̌������v��
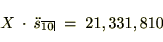
���̊z�̎c��̂P�O�N�Ԃ̂Q���̌������v��
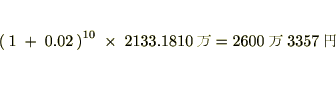
���z��
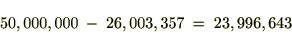
���̋��߂�ꂽ���z�ɑ��Ďc��̊��Ԃ̂P�O�N�Ԃ̊��n�����N���I�������߂܂��B
�N���Q���^�p�ł̂P�O�N�Ԃ̊��n�����N���I���́A
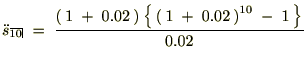
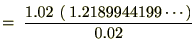
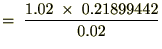
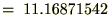
�����ύX��̎c��̋��z��B�����邽�߂̖��N�n�߂ɗp�ӂ�����z�����x��
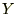 �ƒu���܂��B
�ƒu���܂��B
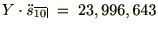
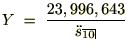
�@�@�@�@
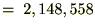
���ۂ̌l�����ƂƂ��Ẳ^�p�����l��
��{�I�ɔN�̎n�߂ɂ��̌�ɉ^�p������z���{�����Ɨp�ӂ���Ƃ��Ă��܂����A���Ƃ��ƒ~��������l�͕ʂƂ��Ď��ۂɂ͂��������ȒP�ɂ��ꂾ���̋��z�������Ȃ�p�ӂ���͓̂�����A�܂����Ƃ������p�ӂ��邾���̒~�����������Ƃ��Ă��A��ʓI�ȎЉ�������Ă���l�ł���A�����̋��^���琶����Ȃǂ̃R�X�g���������������������~�ɉĂ���ꍇ���قƂ�ǂ��Ǝv���܂��B
�v����ɒ~��������]�T����l�ł��싅�I��̂悤�ȔN�_���ł��Ȃ�����A�����Ȃǂɉ���z���������Ƃɔ������Ă���͂��ł��B
�g���͋��Ȃ�h�Ƃ������t�������悤�ɁA�I���W���ŋ��߂�ꂽ���z�����܂�܂ł��̂܂܈�N�Ԃɂ��n���Ď����点��Ƃ����悤�ȍs�ׂ́A��͂�{���]�|�ƌ��킴��܂���B
�Ȃ̂Ŋ��n�����N���I���ɂ�����N����
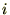 �����̂悤�ɂ��Ă݂܂��B
�����̂悤�ɂ��Ă݂܂��B
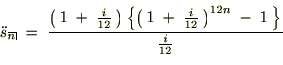

��������L�̗�̂悤�Ȗ��N�N���T���ʼn^�p�������邱�Ƃ̓v���ł��Ȃ��Ȃ�����A��ʂ̕��ł͂Ȃ�����̂��Ƃ炵���ł��B
�O�������N�F���U�����ŔN���R���̉^�p��ڎw��
��L�̃����N��̓��e���ƂT���ł̉^�p�͓���Ƃ��R���ł̉^�p�Ȃ������x�͖ڎw����炵���Ƃ̂��ƁB
���ɖڕW�z��2�`3000���قǂƂ��A������R�O�N���炢������Ƃ����ꍇ�͂R�`�T���~���x�̖����̐ϗ��ɂȂ�܂������S�Ȃ�����������ɂ͂��ꂮ�炢�̋��z�������I�Ȃ̂������ł��B
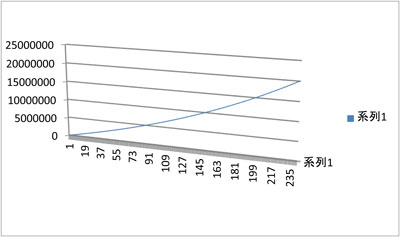
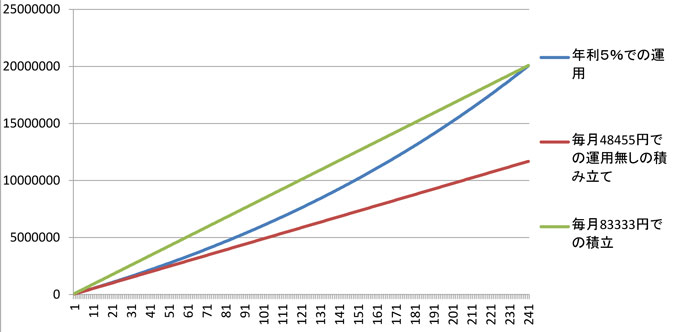
���ۂɎ茳�ɂ���N���I���W���G�N�Z���V�[�g���g���ĔN�����R���łR�O�N�ԉ^�p�̖ڕW�z�R�O�O�O���~�Ƃ����ꍇ�A�����̐ϗ��z���v�Z����Ɩ�5���~�Ƃ������z�ɂȂ�܂��B
�^�p���Ȃ��ꍇ�Ɣ�ׂ�Ɩ���3���~���̈Ⴂ���o�Ă��܂����A�����̂��ƂƂȂ�Ƃ�͂菭�Ȃ����z�Ƃ͌����܂���B
���Ȃ݂ɂ��̐����͐����ی����w�̕���ɂȂ�A�t�@�C�i���V�����v�����i�[�ł���Α��̏ꍇ�͂悭�m��ꂽ�����ɂȂ�܂��i�R�������ɂ悭�o��炵���A���̂Ƃ��������Əo�܂����B�j�B
�����͂Ƃ�킯��������w�̒m���͎g���Ă��܂���̂ŃO���t�\�����ł���悤�ȌW���Z�o�̊ȒP�ȃG�N�Z���V�[�g�Ȃǂ��������ō���Ă݂�̂��ʔ������Ǝv���܂��B
�������A�����i���Ɋ����j�͂����܂Ŏ��ȐӔC�ʼn�����낵�����Ȃ����\���グ�܂��B
�N���I���W���֘A�y�[�W
- ���[�����g���(�ϗ����)
- ���T�C�g�͎�ɕ����Ɋւ��鐔�w�ȂǁA���̑����ӂ��܂߂����X�������ς̃E�F�u�T�C�g�ł��B ���w����Ɋւ��Ă̎�|�Ƃ��ẮA�ʏ�̃e�L�X�g�ł͊�������Ă��܂����e�Ȃǂ��ڂ����L�q���A����ɂ͓������������̂ł͂Ȃ��A�킩��ɂ������e�������ɂ킩��₷���`���邩���ȂǁA�����������E�F�u�R���e���c�Ȃ�ł̗͂����Ƌ@�����������T�C�g�쐬�����Ƃ��Ă��܂��B























